25第二十三章 图形的旋转
文档属性
| 名称 | 25第二十三章 图形的旋转 |  | |
| 格式 | zip | ||
| 文件大小 | 626.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-06 18:46:07 | ||
图片预览




文档简介
(共22张PPT)
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第1课时 图形的旋转
断课导人自主预习检测预习效釆
(一)学习目标
1.理解旋转的有关概念和性质.
2.能够按要求作出简单平面图形经过旋转后的
图形,能利用旋转进行图案设计.
(二)课前预习
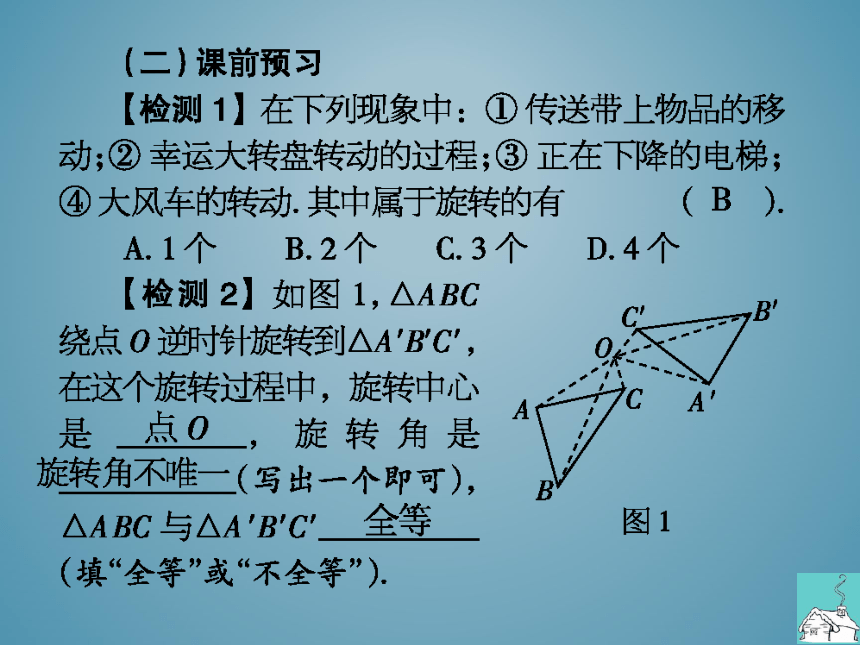
【检测1】在下列现象中:①传送带上物品的移
动;②幸运大转盘转动的过程;③正在下降的电梯;
④大风车的转动.其中属于旋转的有
).
A.1个B.2个C.3个D.4个
【检测2】如图1,△ABC
B
绕点O逆时针旋转到△A'B'C',
在这个旋转过程中,旋转中心
C A
是
旋转角是
(写出一个即可),B
△ABC与△A'B'C
冬1
(填“全等”或“不全等”)
三典型何题典例新,名师点拨解疑
★旋转中心、旋转角、对应点的识别及运用旋转
的性质计算
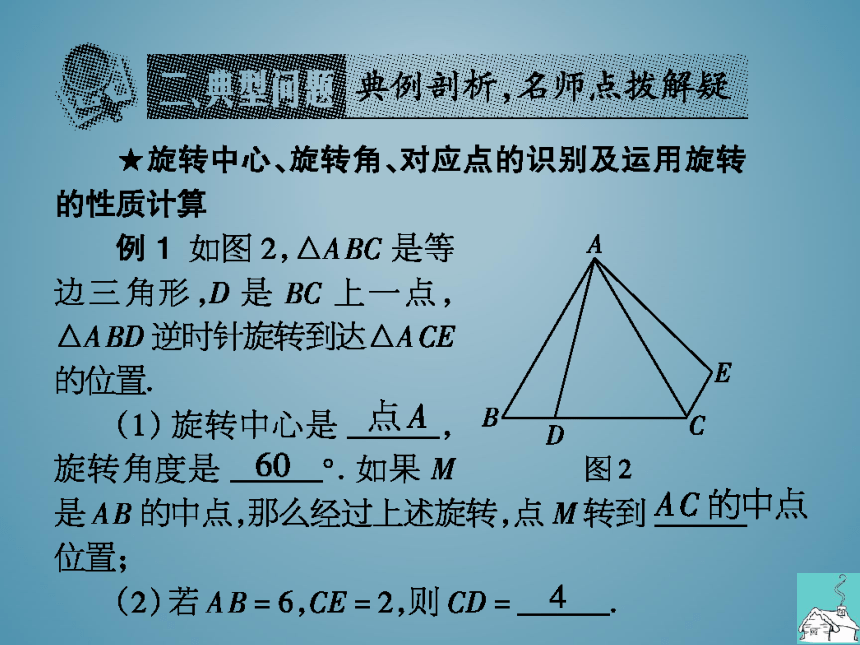
例1如图2,△ABC是等
边三角形,D是BC上一点
△ABD逆时针旋转到达△ACE
的位置
E
(1)旋转中心是
旋转角度是
°.如果M
图2
是AB的中点,那么经过上述旋转,点M转到
位置;
(2)若AB=6,CE=2,则CD
分析:(1)根据题意和等边三角形的性质,很容
易得出旋转中心,旋转角和点M旋转以后的位置;
(2)根据旋转的性质,旋转前、后的图形全等,可求出
BD的长度,进而求出CD的长度
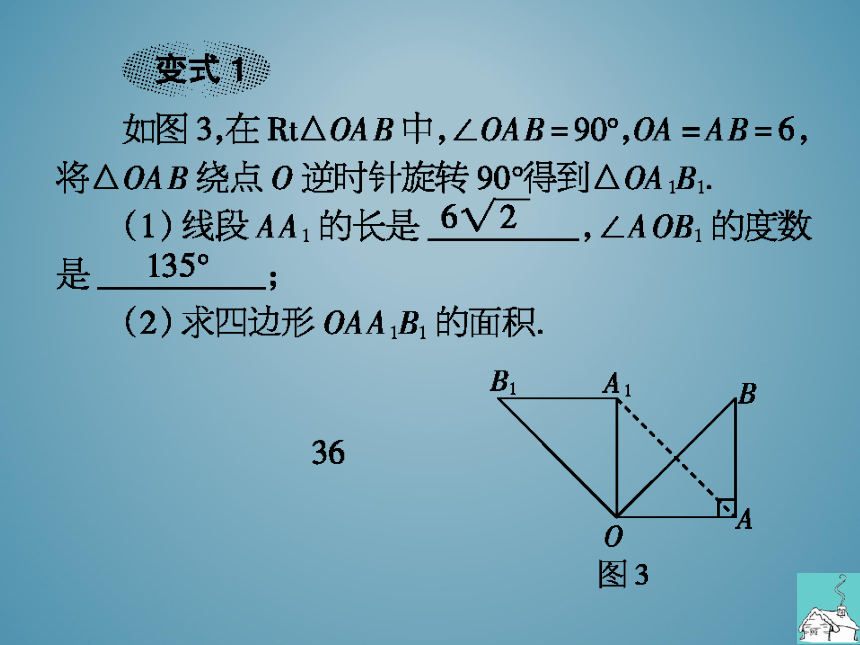
变式
如图3,在Rt△OAB中,∠OAB=909,OA=AB=6,
将△OAB绕点O逆时针旋转90°得到△OA1B1
(1)线段AA1的长是
,∠AOB1的度数
是
(2)求四边形OA1B1的面积
★运用旋转的性质画图
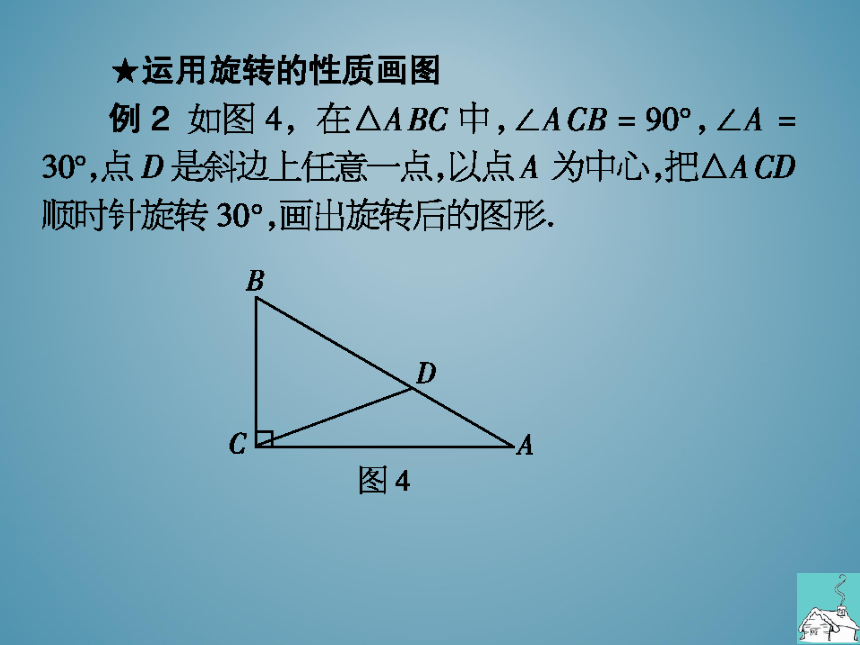
例2如图4,在△ABC中,∠ACB=90,∠A=
309,点D是余边上任意一点,以点A为中心,把△ACD
顺时针旋转30,画出旋转后的图形
分析:关键是确定△ACD旋转后各顶点的对应
点.设得到的三角形是△AEF,点A的对应点是点A,
点C的对应点F在AB上,由AF=AC得点F在AB
的上方作∠DAE=30°,使AE=AD,得点E,连接EF,
△AEF即为所求
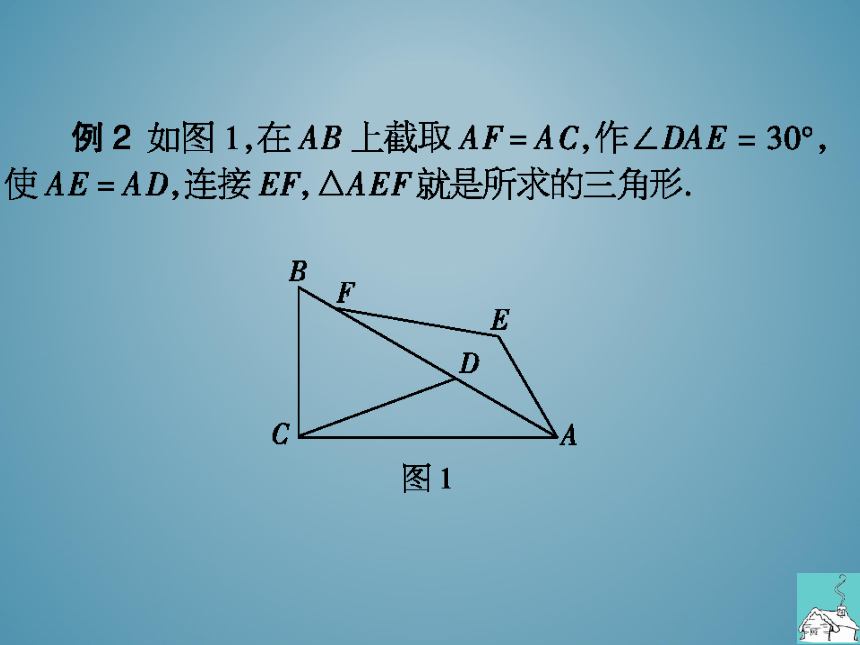
例2如图1,在AB上截取AF=AC,作∠DAE=30°
使AE=AD,连接EF,△AEF就是所求的三角形
B e
E
D
C
图
变式2
如图5,画出△ABO绕点O顺时针旋转90后得
到的△A'B'O,并以点O为原点、每个小方格的长度
为单位长度建立平面直角坐标系,求出点A'的坐标
图5
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第1课时 图形的旋转
断课导人自主预习检测预习效釆
(一)学习目标
1.理解旋转的有关概念和性质.
2.能够按要求作出简单平面图形经过旋转后的
图形,能利用旋转进行图案设计.
(二)课前预习
【检测1】在下列现象中:①传送带上物品的移
动;②幸运大转盘转动的过程;③正在下降的电梯;
④大风车的转动.其中属于旋转的有
).
A.1个B.2个C.3个D.4个
【检测2】如图1,△ABC
B
绕点O逆时针旋转到△A'B'C',
在这个旋转过程中,旋转中心
C A
是
旋转角是
(写出一个即可),B
△ABC与△A'B'C
冬1
(填“全等”或“不全等”)
三典型何题典例新,名师点拨解疑
★旋转中心、旋转角、对应点的识别及运用旋转
的性质计算
例1如图2,△ABC是等
边三角形,D是BC上一点
△ABD逆时针旋转到达△ACE
的位置
E
(1)旋转中心是
旋转角度是
°.如果M
图2
是AB的中点,那么经过上述旋转,点M转到
位置;
(2)若AB=6,CE=2,则CD
分析:(1)根据题意和等边三角形的性质,很容
易得出旋转中心,旋转角和点M旋转以后的位置;
(2)根据旋转的性质,旋转前、后的图形全等,可求出
BD的长度,进而求出CD的长度
变式
如图3,在Rt△OAB中,∠OAB=909,OA=AB=6,
将△OAB绕点O逆时针旋转90°得到△OA1B1
(1)线段AA1的长是
,∠AOB1的度数
是
(2)求四边形OA1B1的面积
★运用旋转的性质画图
例2如图4,在△ABC中,∠ACB=90,∠A=
309,点D是余边上任意一点,以点A为中心,把△ACD
顺时针旋转30,画出旋转后的图形
分析:关键是确定△ACD旋转后各顶点的对应
点.设得到的三角形是△AEF,点A的对应点是点A,
点C的对应点F在AB上,由AF=AC得点F在AB
的上方作∠DAE=30°,使AE=AD,得点E,连接EF,
△AEF即为所求
例2如图1,在AB上截取AF=AC,作∠DAE=30°
使AE=AD,连接EF,△AEF就是所求的三角形
B e
E
D
C
图
变式2
如图5,画出△ABO绕点O顺时针旋转90后得
到的△A'B'O,并以点O为原点、每个小方格的长度
为单位长度建立平面直角坐标系,求出点A'的坐标
图5
同课章节目录
