30第二十四章 垂直于弦的直径
文档属性
| 名称 | 30第二十四章 垂直于弦的直径 |  | |
| 格式 | zip | ||
| 文件大小 | 586.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-06 18:46:07 | ||
图片预览







文档简介
(共24张PPT)
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第2课时 垂直于弦的直径
二新课导人自主预习,检测预习效果
学习目标
1.理解圆的对称性
2.掌握垂径定理及其推论,会用它们解决简单的
实际问题
(二)课前预习
检测1】如图1,CD是⊙O
的直径,点C是AB的中点,下列结A
B
论中错误的是
A.点D是ADB的中点
B.CD⊥AB
C.CD平分AB
图1
D.AB平分CD
检测2】已知AB是⊙O的直径,弦CD与AB
相交于点E,若使CB=B,则还需添加条件
(填出一个即可).
二
典型问题婆例剖析,名师点拨解疑
★垂径定理的简单应用
例1“今有圆材,理在壁中,不知大小,以锯锯
之,深一寸,锯道长一尺,问径几何”.这是《九章算术》
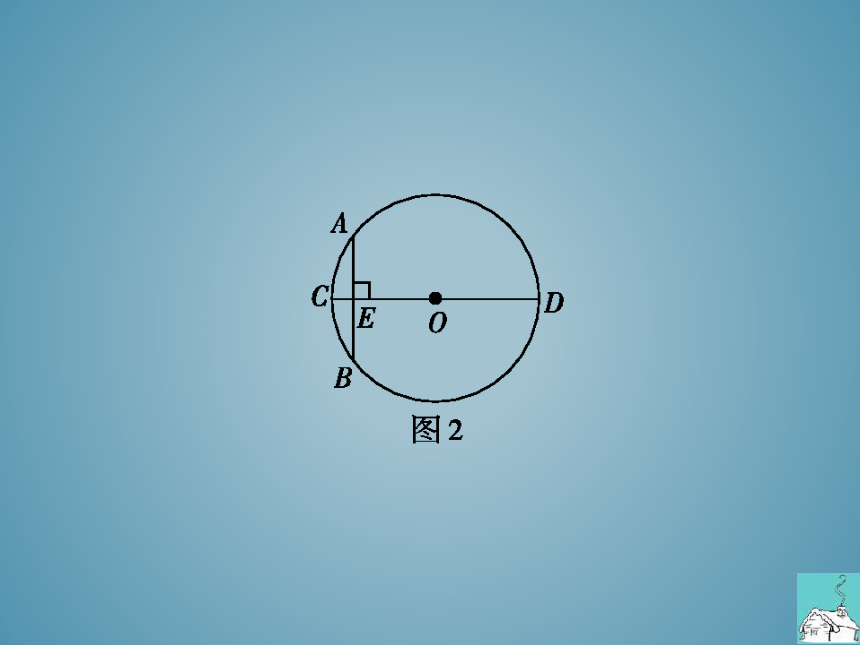
中的问题,用数学语言可表述为:如图2,CD为⊙O
的直径,弦AB⊥CD于点E,CE=1寸,AB=10寸,那
么直径CD的长是多少
分析:利用垂径定理和勾股定理列方程求解即可
例1连接OA.设OA=x,则OE=x-1
AB⊥CD,AB=10,AE=5
于是x2-(x-1)2=532解得x=13
CD=26(寸)
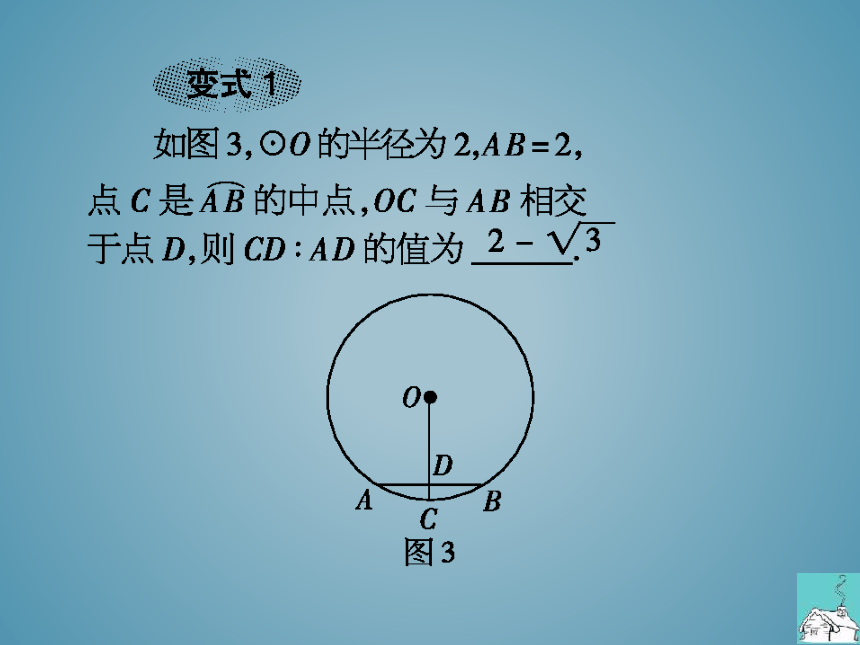
变式博
如图3,⊙0的半径为2,AB=2,
点C是AB的中点,OC与AB相交
于点D,则CD:AD的值为
例2如图4,⊙O的半径为2V5,弦AB和弦
CD互相垂直,点P是垂足.若AB=8,CD=6,求OP
的长
分析:求出圆心到两条弦的距离,然后用勾般定
理求OP的长
B
D
图4
例2作OM⊥AB于点M,ON⊥CD于点N,由垂径定
理,得OM2=(2V5)2-42=4,ON=(2V5)2-32=11
又易证四边形MONP是矩形,
OP=√OM2+ON=V15
变式2
如图5,∠P的两边与⊙O相交于点A,B,C,D,
员心O在∠P的平分线上求证AB=CD
B
●O
D
图5
变式2过点O作OE⊥AB于点E,OF⊥CD于点F,
连接OA,OC.由垂径定理,得AB=2AE,CD=2CF
圆心O在∠P的平分线上,∵OE=OF.
OA=OC,∵Rt△OAE≌Rt△OCF
AE=CF∵AB=CD
E明镇办结回咪反忍,领才能提高
1.圆是轴对称图形,任何一条
所在的直
线都是它的对称轴.
2.垂直于弦的
平分弦,并且平分弦所对
的两条弧.平分弦(
)的直径垂直于弦,并
且平分弦所对的两条弧
3.一条直线,如果以下列五个论断中的任意两个
做条件,那么余下的三个即是正确结论这五个论断
是:(1)经过圆心;(2)垂直于弦;(3)平分弦(不是直
径);(4)平分弦所对的劣弧;(5)平分弦所对的优弧
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第2课时 垂直于弦的直径
二新课导人自主预习,检测预习效果
学习目标
1.理解圆的对称性
2.掌握垂径定理及其推论,会用它们解决简单的
实际问题
(二)课前预习
检测1】如图1,CD是⊙O
的直径,点C是AB的中点,下列结A
B
论中错误的是
A.点D是ADB的中点
B.CD⊥AB
C.CD平分AB
图1
D.AB平分CD
检测2】已知AB是⊙O的直径,弦CD与AB
相交于点E,若使CB=B,则还需添加条件
(填出一个即可).
二
典型问题婆例剖析,名师点拨解疑
★垂径定理的简单应用
例1“今有圆材,理在壁中,不知大小,以锯锯
之,深一寸,锯道长一尺,问径几何”.这是《九章算术》
中的问题,用数学语言可表述为:如图2,CD为⊙O
的直径,弦AB⊥CD于点E,CE=1寸,AB=10寸,那
么直径CD的长是多少
分析:利用垂径定理和勾股定理列方程求解即可
例1连接OA.设OA=x,则OE=x-1
AB⊥CD,AB=10,AE=5
于是x2-(x-1)2=532解得x=13
CD=26(寸)
变式博
如图3,⊙0的半径为2,AB=2,
点C是AB的中点,OC与AB相交
于点D,则CD:AD的值为
例2如图4,⊙O的半径为2V5,弦AB和弦
CD互相垂直,点P是垂足.若AB=8,CD=6,求OP
的长
分析:求出圆心到两条弦的距离,然后用勾般定
理求OP的长
B
D
图4
例2作OM⊥AB于点M,ON⊥CD于点N,由垂径定
理,得OM2=(2V5)2-42=4,ON=(2V5)2-32=11
又易证四边形MONP是矩形,
OP=√OM2+ON=V15
变式2
如图5,∠P的两边与⊙O相交于点A,B,C,D,
员心O在∠P的平分线上求证AB=CD
B
●O
D
图5
变式2过点O作OE⊥AB于点E,OF⊥CD于点F,
连接OA,OC.由垂径定理,得AB=2AE,CD=2CF
圆心O在∠P的平分线上,∵OE=OF.
OA=OC,∵Rt△OAE≌Rt△OCF
AE=CF∵AB=CD
E明镇办结回咪反忍,领才能提高
1.圆是轴对称图形,任何一条
所在的直
线都是它的对称轴.
2.垂直于弦的
平分弦,并且平分弦所对
的两条弧.平分弦(
)的直径垂直于弦,并
且平分弦所对的两条弧
3.一条直线,如果以下列五个论断中的任意两个
做条件,那么余下的三个即是正确结论这五个论断
是:(1)经过圆心;(2)垂直于弦;(3)平分弦(不是直
径);(4)平分弦所对的劣弧;(5)平分弦所对的优弧
同课章节目录
