31第二十四章 弧、弦、圆心角
文档属性
| 名称 | 31第二十四章 弧、弦、圆心角 |

|
|
| 格式 | zip | ||
| 文件大小 | 533.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-06 18:46:07 | ||
图片预览






文档简介
(共24张PPT)
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第3课时 弧、弦、圆心角
上新导人自主预习,检测预习效果
(一)学习目标
1.了解圆心角的概念
2.掌握弧、弦和圆心角的定理及推论.
(二)课前预习
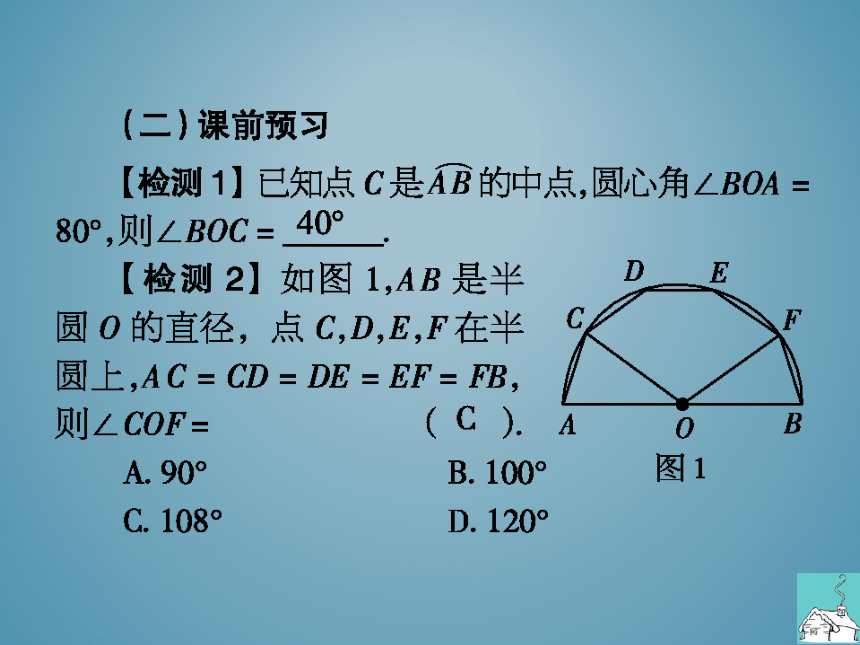
检测1】已知点C是AB的中点,圆心角∠BOA
80°,则∠BOC
检测2】如图1,AB是半
圆O的直径,点C,D,EF在半9
F
员上,AC=CD=DE=EF=PB,
则∠COF
().A
B
A.90°
B.100°
图
C.108°
D.120°
匚典型闻典剑剖析名师点拨解疑
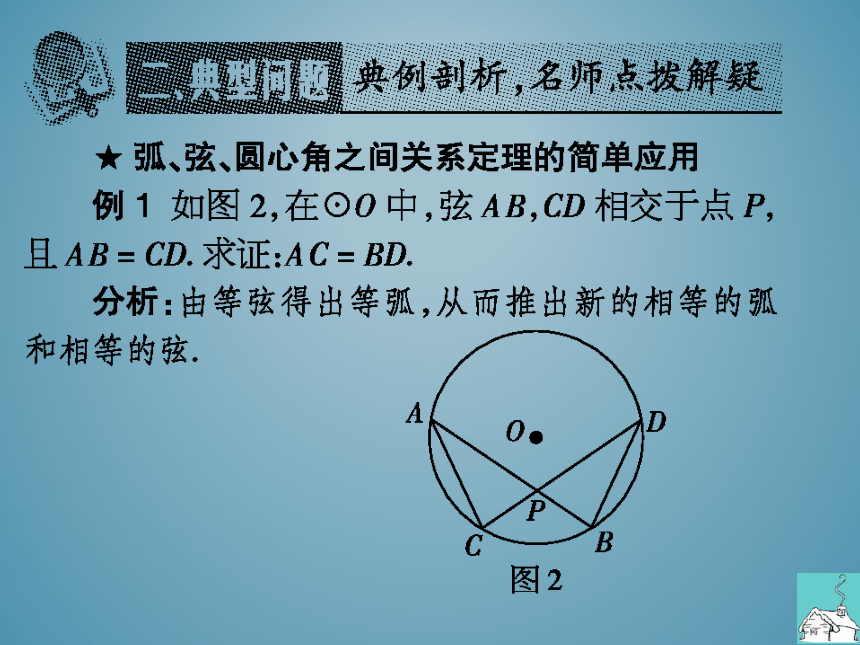
★弧、弦、圆心角之间关系定理的简单应用
例1如图2,在⊙O中,弦AB,CD相交于点P,
且AB=CD求证:AC=BD
分析:由等弦得出等弧,从而推出新的相等的弧
和相等的弦
B
图2
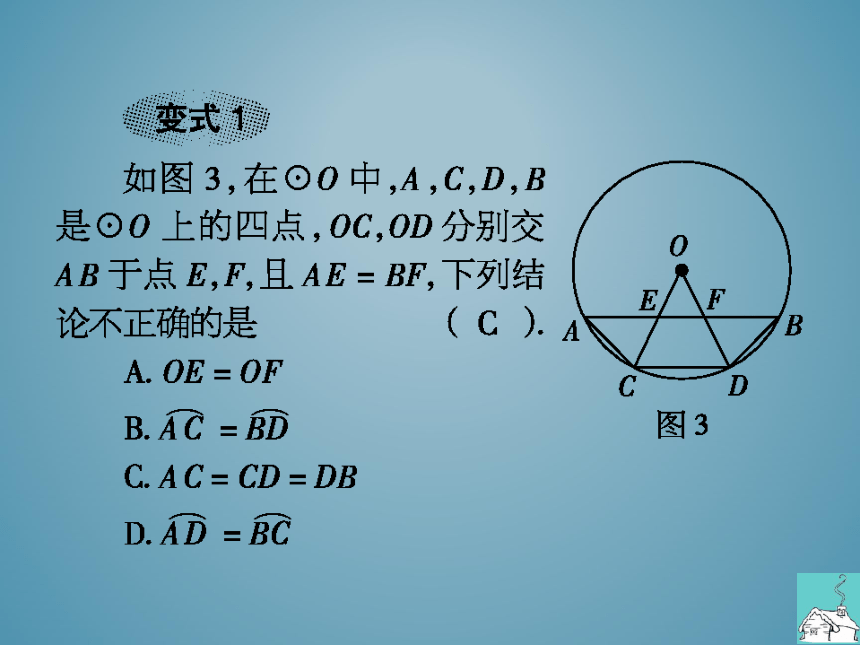
变式1
如图3,在⊙O中,A,C,D,B
是⊙O上的四点,OC,OD分别交
AB于点E,F,且AE=BF,下列结
E/\F
论不正确的是
B
A OE= OF
C
B.ACEBD
图3
CAC=CD= DB
DAD=BC
★弧、弦、圆心角之间关系定理的综合应用
例2如图4,以口ABCD的顶点A为圆心、AB为
半径作⊙A,⊙A分别交AD,BC于点E,F,延长BA
交⊙A于点G求证:CE=EF
分析:欲证弧相等,只需证弧所对的圆心角相等
这可由平行线的性质和等腰三角形的性质得出
E
F4
C
图
例2连接AF.四边形ABCD是平行四边形,
AD∥BC.∴∠GAE=∠B,∠EAF=∠AFB
∵·AB=AF∴∠B=∠APB.∴∠GAE=∠EAF
GE = EF
变式2
如图5,AB,CD都是⊙O的
B
直径,弦DE∥AB,则与AE相等
的弧是
图5
y三期辅办结回味反思领悟才能提高
1.顶点在圆心的角叫做
2.在同圆或等圆中,相等的圆心角所对的弧
,所对的弦
3.同圆或等圆中,两个圆心角,两条弧,两条弦这
三者中,若有一组量相等,则其余两组量也相等
四阶训练自主练兵,会做才懂了
A组:基础练习
1在同圆中,下列四个命题:①圆心角是顶点在
员心的角;②两个圆心角相等,它们所对的弦也相等;
③两条非直径的弦相等,它们所对的劣弧也相等;
④等弧所对的圆心角相等.其中真命题是().
A.①②③④
B①②④
C②③④
D②④
2.如图6,AB是⊙O的直径,C,D是BE的三等
分点,若∠AOE=60°,则∠COE是
A.40°
B.60
C.80
D.120°
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第3课时 弧、弦、圆心角
上新导人自主预习,检测预习效果
(一)学习目标
1.了解圆心角的概念
2.掌握弧、弦和圆心角的定理及推论.
(二)课前预习
检测1】已知点C是AB的中点,圆心角∠BOA
80°,则∠BOC
检测2】如图1,AB是半
圆O的直径,点C,D,EF在半9
F
员上,AC=CD=DE=EF=PB,
则∠COF
().A
B
A.90°
B.100°
图
C.108°
D.120°
匚典型闻典剑剖析名师点拨解疑
★弧、弦、圆心角之间关系定理的简单应用
例1如图2,在⊙O中,弦AB,CD相交于点P,
且AB=CD求证:AC=BD
分析:由等弦得出等弧,从而推出新的相等的弧
和相等的弦
B
图2
变式1
如图3,在⊙O中,A,C,D,B
是⊙O上的四点,OC,OD分别交
AB于点E,F,且AE=BF,下列结
E/\F
论不正确的是
B
A OE= OF
C
B.ACEBD
图3
CAC=CD= DB
DAD=BC
★弧、弦、圆心角之间关系定理的综合应用
例2如图4,以口ABCD的顶点A为圆心、AB为
半径作⊙A,⊙A分别交AD,BC于点E,F,延长BA
交⊙A于点G求证:CE=EF
分析:欲证弧相等,只需证弧所对的圆心角相等
这可由平行线的性质和等腰三角形的性质得出
E
F4
C
图
例2连接AF.四边形ABCD是平行四边形,
AD∥BC.∴∠GAE=∠B,∠EAF=∠AFB
∵·AB=AF∴∠B=∠APB.∴∠GAE=∠EAF
GE = EF
变式2
如图5,AB,CD都是⊙O的
B
直径,弦DE∥AB,则与AE相等
的弧是
图5
y三期辅办结回味反思领悟才能提高
1.顶点在圆心的角叫做
2.在同圆或等圆中,相等的圆心角所对的弧
,所对的弦
3.同圆或等圆中,两个圆心角,两条弧,两条弦这
三者中,若有一组量相等,则其余两组量也相等
四阶训练自主练兵,会做才懂了
A组:基础练习
1在同圆中,下列四个命题:①圆心角是顶点在
员心的角;②两个圆心角相等,它们所对的弦也相等;
③两条非直径的弦相等,它们所对的劣弧也相等;
④等弧所对的圆心角相等.其中真命题是().
A.①②③④
B①②④
C②③④
D②④
2.如图6,AB是⊙O的直径,C,D是BE的三等
分点,若∠AOE=60°,则∠COE是
A.40°
B.60
C.80
D.120°
同课章节目录
