32第二十四章 圆周角
图片预览




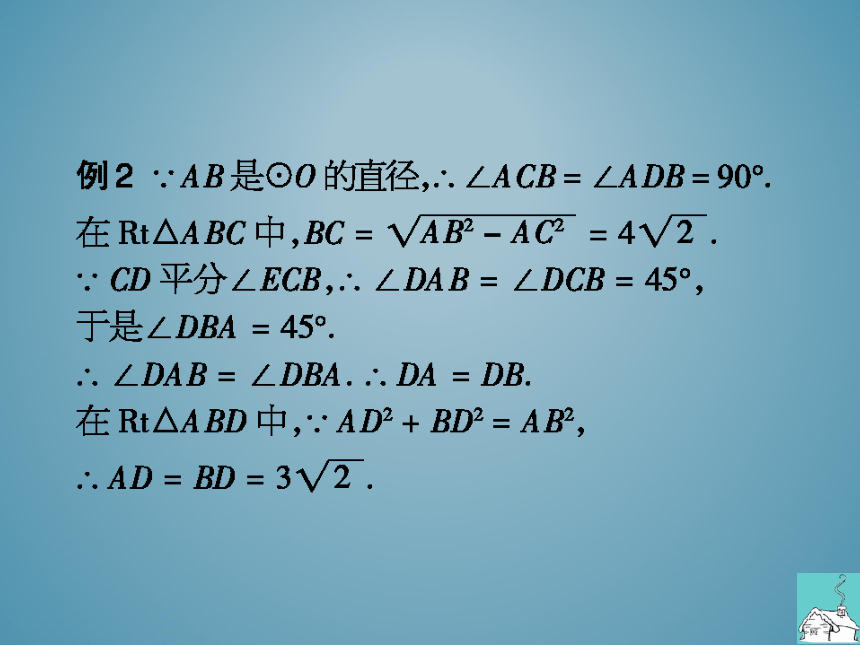
文档简介
(共21张PPT)
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第4课时 圆周角
新课导人自主预习检测预习效果
(一)学习目标
1.理解圆周角、圆内接多边形、多边形的外接圆
等概念
2.掌握圆周角定理及其推论,并能运用它们进行
计算和证明.
(二)课前预习
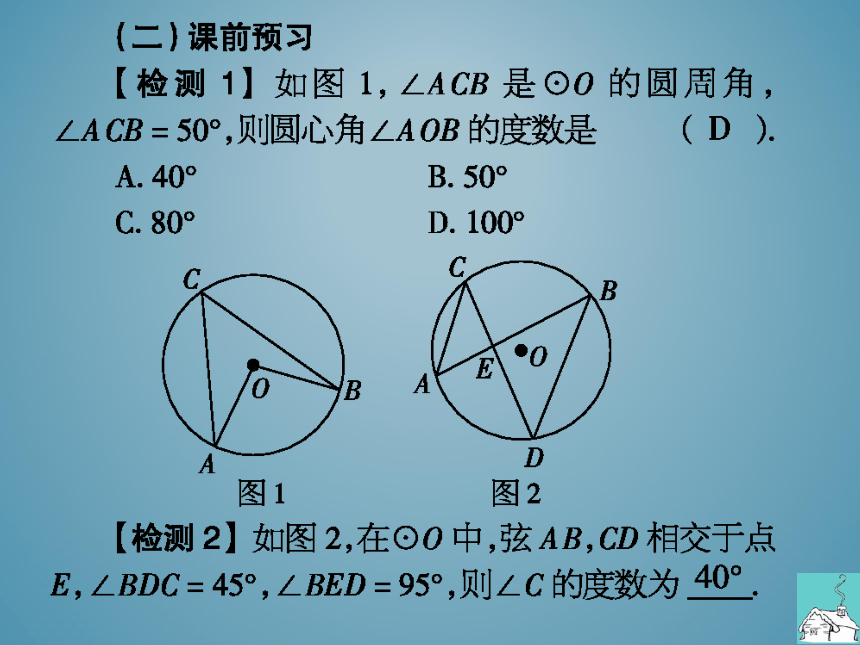
检测1】如图1,∠ACB是⊙0的圆周角,
∠ACB=50°,则圆心角∠AOB的度数是(
A.40°
B.50°
C.80°
D.100°
B
BE°0
A
D
图1
图2
检测2】如图2,在⊙O中,弦AB,CD相交于点
E,∠BDC=45°,∠BED=95°,则∠C的度数为
型问懸典例剖析,名师点拨解疑
★圆周角定理的应用
例1如图3,△ABC的高AD,BF相交于点H,
AD的延长线交△ABC的外接圆于点E,求证:DH=
DE
分析:欲证DH=DE,需证△BDH≌△BDE,这可
用“角边角”证出
丑AF
B
E
图3
例1连接BE.AD,BF是△ABC的高,
∴∠BC+∠C=90°,∠CAD+∠C=90°
∠FBC=∠CAD
∴∠CBE=∠CAD,∠PBC=∠CBE
又∵BD=BD,∠BDH=∠BDE=90°,
△BD≌△BDE.DH=DE
变式稳
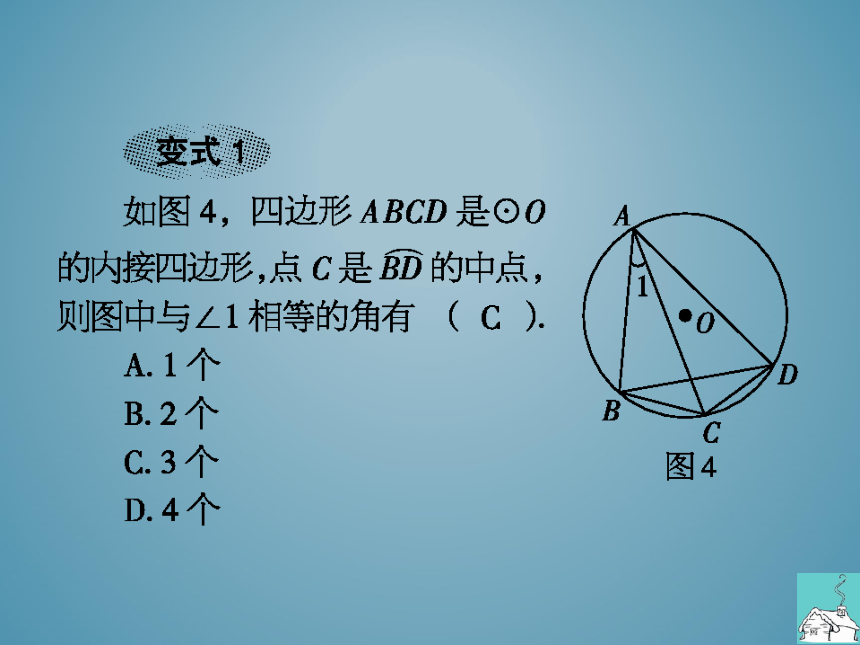
如图4,四边形ABCD是⊙O
的内接四边形,点C是BD的中点
贝图中与∠1相等的角有()
A.1
个个个
D
B.2
B
图4
D.4个
★圆周角定理推论的应用
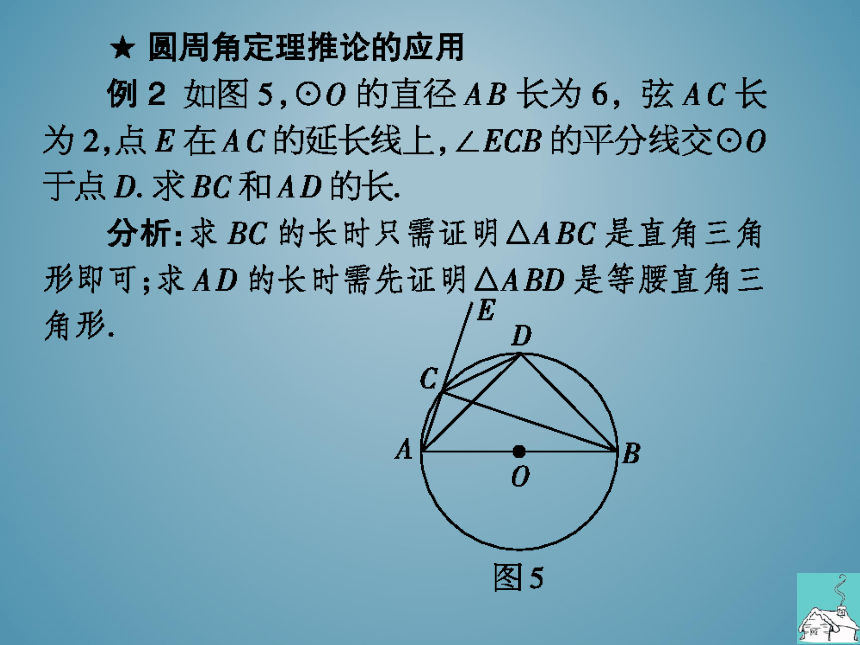
例2如图5,⊙O的直径AB长为6,弦AC长
为2,点E在AC的延长线上,∠ECB的平分线交⊙O
于点D求BC和AD的长
分析:求BC的长时只需证明△ABC是直角三角
形郎可;求AD的长时需先证明△ABD是等腰直角三
角形
E
D
C.
B
图5
例2:AB是⊙O的直径,∠ACB=∠ADB=909
在Rt△ABC中,BC=AB2-AC2=4V2
CD平分∠ECB,∠DAB=∠DCB=45°,
于是∠DBA=45
∴∠DAB=∠DBA.∴.DA=DB.
在Rt△ABD中,AD2+BD2=AB,
AD=BD=3V2
式
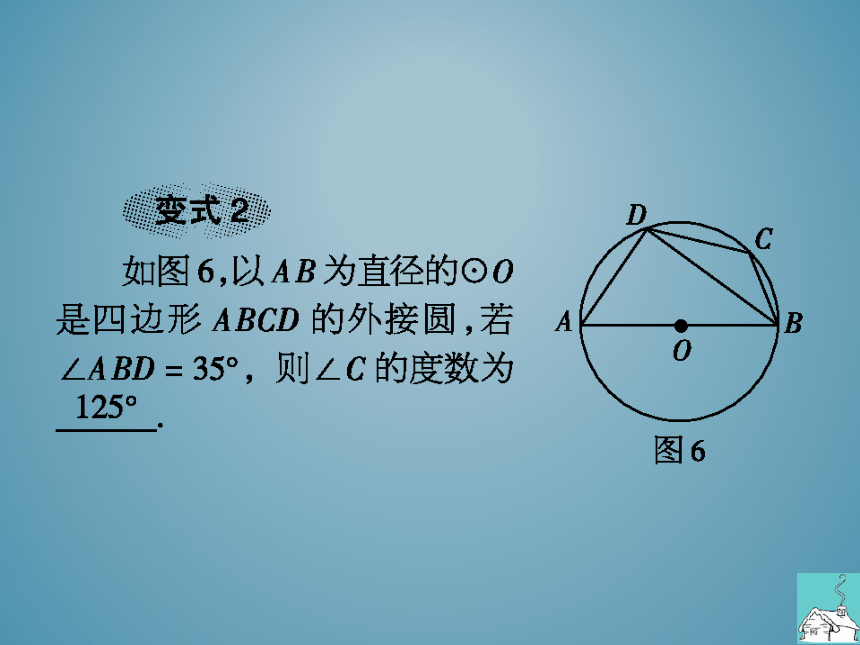
如图6,以AB为直径的⊙O
是四边形ABCD的外接圆,若A
B
∠ABD=35°,则∠C的度数为
0
图6
三厨绵办结回咪反思领悟才能提高
1.顶点在圆上,并且两边都与圆相交的角叫做
2.在同圆或等圆中,同弧或等弧所对的圆周角
,都等于这条弧所对的圆心角的
3.半圆或直径所对的圆周角是,909的圆
周角所对的弦是
4.圆内接四边形的对角
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第4课时 圆周角
新课导人自主预习检测预习效果
(一)学习目标
1.理解圆周角、圆内接多边形、多边形的外接圆
等概念
2.掌握圆周角定理及其推论,并能运用它们进行
计算和证明.
(二)课前预习
检测1】如图1,∠ACB是⊙0的圆周角,
∠ACB=50°,则圆心角∠AOB的度数是(
A.40°
B.50°
C.80°
D.100°
B
BE°0
A
D
图1
图2
检测2】如图2,在⊙O中,弦AB,CD相交于点
E,∠BDC=45°,∠BED=95°,则∠C的度数为
型问懸典例剖析,名师点拨解疑
★圆周角定理的应用
例1如图3,△ABC的高AD,BF相交于点H,
AD的延长线交△ABC的外接圆于点E,求证:DH=
DE
分析:欲证DH=DE,需证△BDH≌△BDE,这可
用“角边角”证出
丑AF
B
E
图3
例1连接BE.AD,BF是△ABC的高,
∴∠BC+∠C=90°,∠CAD+∠C=90°
∠FBC=∠CAD
∴∠CBE=∠CAD,∠PBC=∠CBE
又∵BD=BD,∠BDH=∠BDE=90°,
△BD≌△BDE.DH=DE
变式稳
如图4,四边形ABCD是⊙O
的内接四边形,点C是BD的中点
贝图中与∠1相等的角有()
A.1
个个个
D
B.2
B
图4
D.4个
★圆周角定理推论的应用
例2如图5,⊙O的直径AB长为6,弦AC长
为2,点E在AC的延长线上,∠ECB的平分线交⊙O
于点D求BC和AD的长
分析:求BC的长时只需证明△ABC是直角三角
形郎可;求AD的长时需先证明△ABD是等腰直角三
角形
E
D
C.
B
图5
例2:AB是⊙O的直径,∠ACB=∠ADB=909
在Rt△ABC中,BC=AB2-AC2=4V2
CD平分∠ECB,∠DAB=∠DCB=45°,
于是∠DBA=45
∴∠DAB=∠DBA.∴.DA=DB.
在Rt△ABD中,AD2+BD2=AB,
AD=BD=3V2
式
如图6,以AB为直径的⊙O
是四边形ABCD的外接圆,若A
B
∠ABD=35°,则∠C的度数为
0
图6
三厨绵办结回咪反思领悟才能提高
1.顶点在圆上,并且两边都与圆相交的角叫做
2.在同圆或等圆中,同弧或等弧所对的圆周角
,都等于这条弧所对的圆心角的
3.半圆或直径所对的圆周角是,909的圆
周角所对的弦是
4.圆内接四边形的对角
同课章节目录
