34第二十四章 点和圆的位置关系
文档属性
| 名称 | 34第二十四章 点和圆的位置关系 |  | |
| 格式 | zip | ||
| 文件大小 | 579.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-06 18:46:07 | ||
图片预览








文档简介
(共22张PPT)
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第5课时 点和圆的位置关系
新课导人自主预习,检测预习效果
(一)学习目标
1.掌握点和圆的位置关系,知道圆大、圆上、圆外
分别由满足什么条件的点组成
2.会作三角形外接圆的圆心或圆弧所在圆的圆
心玊解三角形的外接圆外心等概念
3.了解反证法的基木思路和一般步骤
(二)课前预习
检测1】已知⊙O的半径为4cm,
(1)若点A在⊙O上,则OA
(2)若点B在⊙O内,则OB=
(3)若点C在⊙O外,则OC=
(填写一个
符合题意的结果即可)
检测2】如图1,知直线L和A,B两点,求作
经过A,B两点的圆,使圆心在直线L上(用尺规作图,
保留作图痕迹,不写作法,不必证明)
检测2】提示:(1)连接AB;(2)作AB的垂直平分
线交l点O;(3)以点O为圆心,OA为半径画圆.⊙O即
为所求图略.
二典型问题典例剖析,名师点拨解疑
★判断点与圆的位置关系
例1如图2,在△ABC中,∠ACB=90°,BC
5cm,AC=12cm,CD为斜边AB上的中线,以C为
圆心,以65cm为半径作圆,则点A,B,D与⊙C的位
置关系如何
分析:通过比较点到圆心的距离和圆的半径之间
的大小关系,判断点与圆的位置关系
例1∵AB=V52+122=13,
CD=13=65:点D在⊙C上
2
5<65,点B在⊙C内
∵12>65,点A在⊙C外
如图3,两个以点O为圆心的同心圆,大圆的半
径为5cm,小圆的半径为3cm,点A为阴影部分(即
圆环)中的一点,则OA可以为
cm(写出
个满足条件的值即可)
0
图3
★作三角形的外接圆
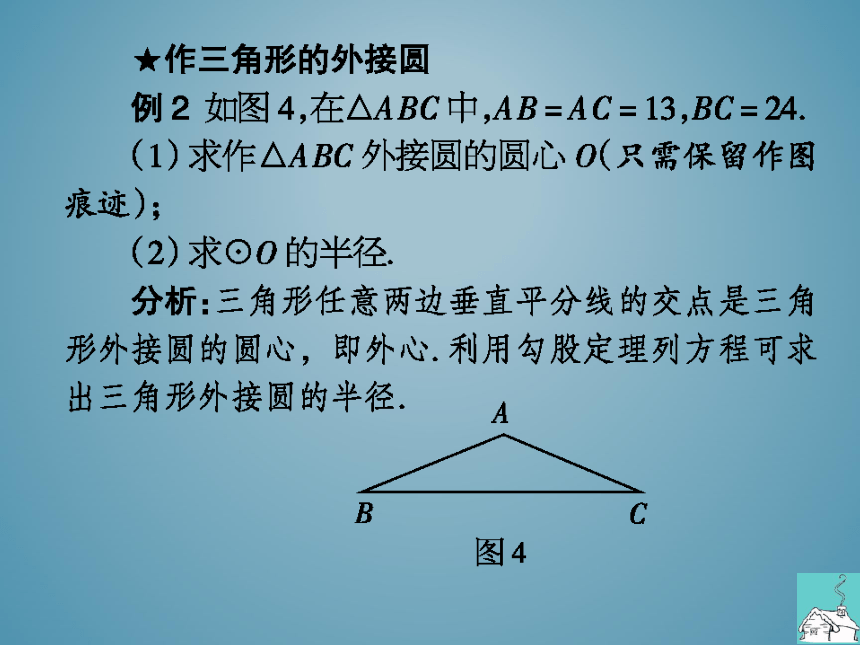
例2如图4,在△ABC中,AB=AC=13,BC=24
(1)求作△ABC外接圆的圆心O(只需保留作图
痕迹);
(2)求⊙O的半径
分析:三角形任意两边垂直平分线的交点是三角
形外接圆的圆心,即外心.利用勾股定理列方程可求
出三角形外接圆的半径
例2(1)略;
(2)设AO交BC于点D,⊙O的半径为x
则OA⊥BC,BD=12.
在Rt△ABD中,AD=V132-122=5
设OA=x,则OB=x,OD=x-5
在R△OBD中,x2-(x-5)2=12.解得x=169
△ABC外接圆的半径是169
变式2
在△ABC中,AB=AC,BC=8,△ABC外接圆的
半径为5,则BC边上的高等于
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第5课时 点和圆的位置关系
新课导人自主预习,检测预习效果
(一)学习目标
1.掌握点和圆的位置关系,知道圆大、圆上、圆外
分别由满足什么条件的点组成
2.会作三角形外接圆的圆心或圆弧所在圆的圆
心玊解三角形的外接圆外心等概念
3.了解反证法的基木思路和一般步骤
(二)课前预习
检测1】已知⊙O的半径为4cm,
(1)若点A在⊙O上,则OA
(2)若点B在⊙O内,则OB=
(3)若点C在⊙O外,则OC=
(填写一个
符合题意的结果即可)
检测2】如图1,知直线L和A,B两点,求作
经过A,B两点的圆,使圆心在直线L上(用尺规作图,
保留作图痕迹,不写作法,不必证明)
检测2】提示:(1)连接AB;(2)作AB的垂直平分
线交l点O;(3)以点O为圆心,OA为半径画圆.⊙O即
为所求图略.
二典型问题典例剖析,名师点拨解疑
★判断点与圆的位置关系
例1如图2,在△ABC中,∠ACB=90°,BC
5cm,AC=12cm,CD为斜边AB上的中线,以C为
圆心,以65cm为半径作圆,则点A,B,D与⊙C的位
置关系如何
分析:通过比较点到圆心的距离和圆的半径之间
的大小关系,判断点与圆的位置关系
例1∵AB=V52+122=13,
CD=13=65:点D在⊙C上
2
5<65,点B在⊙C内
∵12>65,点A在⊙C外
如图3,两个以点O为圆心的同心圆,大圆的半
径为5cm,小圆的半径为3cm,点A为阴影部分(即
圆环)中的一点,则OA可以为
cm(写出
个满足条件的值即可)
0
图3
★作三角形的外接圆
例2如图4,在△ABC中,AB=AC=13,BC=24
(1)求作△ABC外接圆的圆心O(只需保留作图
痕迹);
(2)求⊙O的半径
分析:三角形任意两边垂直平分线的交点是三角
形外接圆的圆心,即外心.利用勾股定理列方程可求
出三角形外接圆的半径
例2(1)略;
(2)设AO交BC于点D,⊙O的半径为x
则OA⊥BC,BD=12.
在Rt△ABD中,AD=V132-122=5
设OA=x,则OB=x,OD=x-5
在R△OBD中,x2-(x-5)2=12.解得x=169
△ABC外接圆的半径是169
变式2
在△ABC中,AB=AC,BC=8,△ABC外接圆的
半径为5,则BC边上的高等于
同课章节目录
