35第二十四章 直线和圆的位置关系(1)
文档属性
| 名称 | 35第二十四章 直线和圆的位置关系(1) |  | |
| 格式 | zip | ||
| 文件大小 | 678.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-06 18:46:07 | ||
图片预览






文档简介
(共29张PPT)
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第6课时 直线和圆的位置关系(1)
A自主预习,检测预习效果
(一)学习目标
1.从直线与圆的交点个数理解直线与圆的三种
位置关系,了解割线、切线和切点等概念
2.掌握直线与圆的三种位置关系及相应的数量
关系
3.能运用切线的兴定定理证明直线与圆相切
课前预习
检测1】已知⊙O的半径r=5cm,圆心O到直
线L的距离为d,当d
时
直线L与⊙O有公共点(填写一个
答案即可)
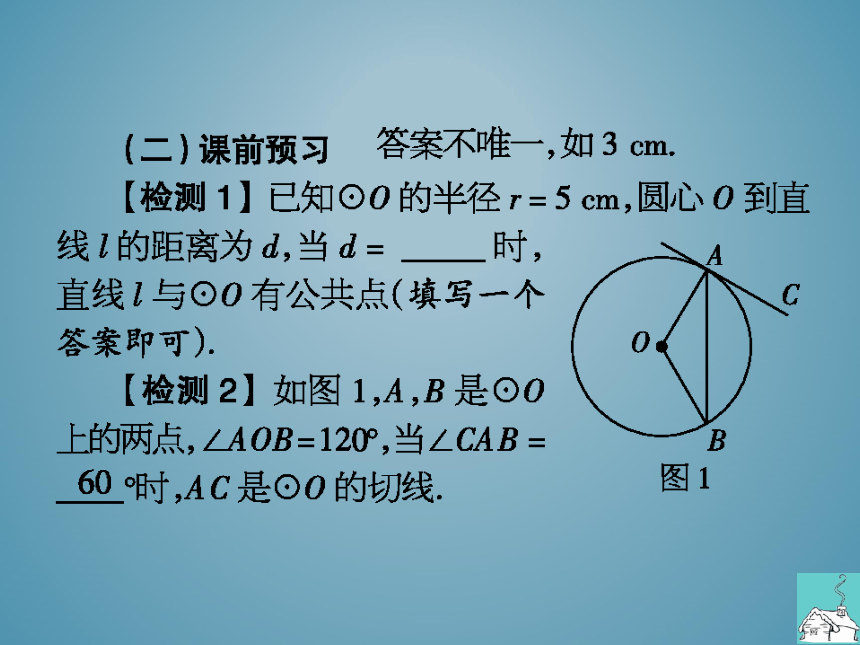
检测2】如图1,A,B是⊙O
上的两点,∠AOB=120°,当∠CAB
B
时,AC是⊙O的切线
图1
参典型问题典例析,名师点拨解媛
★判断直线与圆的位置关系
例1如图2,在△ABC中,BC=2cm,∠B=30°,
∠C=45°.以点A为圆心作⊙A,当半径为多长时,所
作⊙A与直线BC分别有下列位置关系:
(1)相切;
(2)相交;
(3)相离
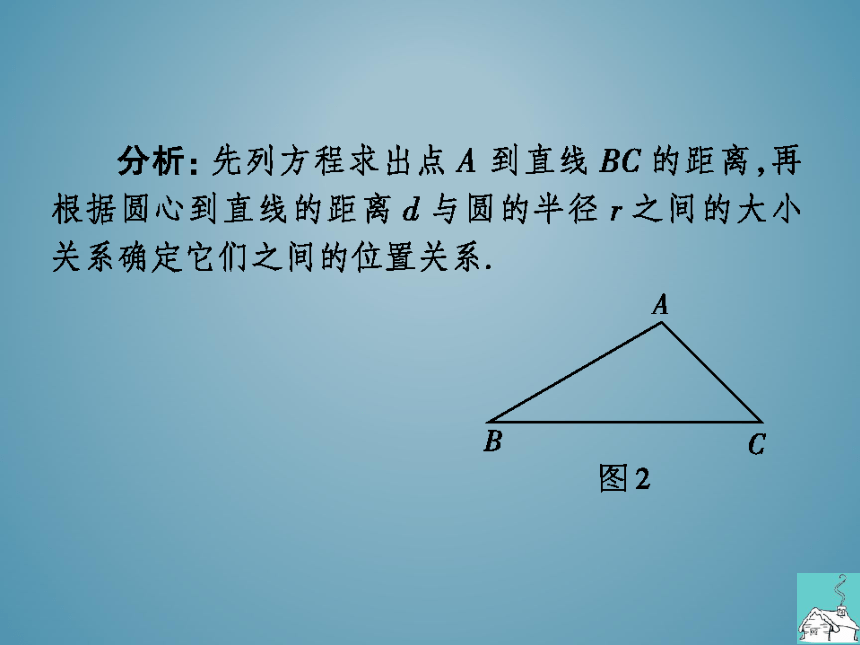
分析:先列方程求出点A到直线BC的距离,再
根据圆心到直线的距离d与圆的半径r之间的大小
关系确定它们之间的位置关系
B
图2
例1过点A作AD⊥BC于点D.
设AD=x,则BD=V3x,DC=x
于是(√3+1)x=2.解得x=V3-1.
(1)当x=(V3-1)cm时,⊙A与直线BC相切;
(2)当x>(3-1)cm时,⊙A与直线BC相交;
(3)当x<(3-1)cm时,⊙A与直线BC相离
式
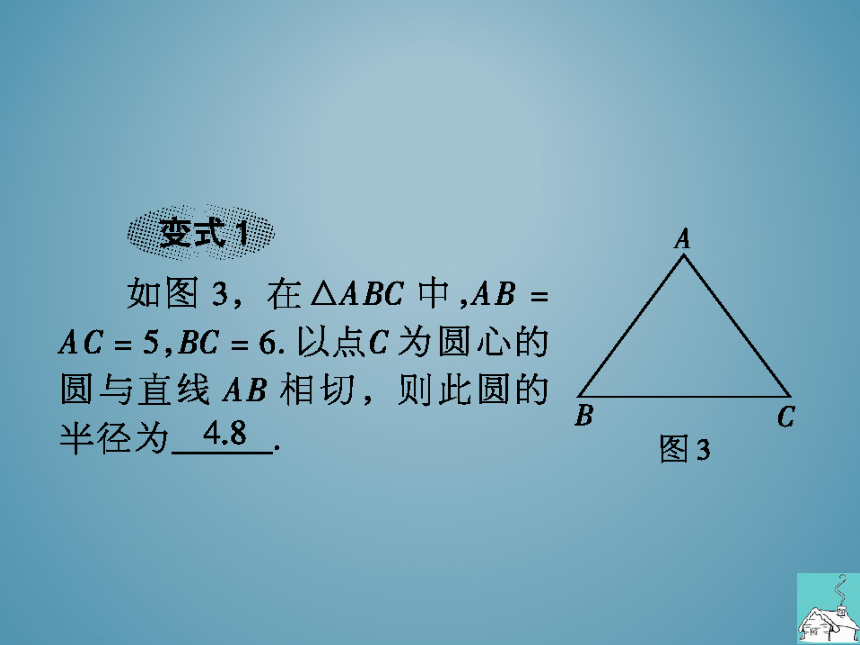
如图3,在△ABC中,AB=
AC=5,BC=6.以点C为圆心的
圆与直线AB相切,则此圆的
半径为
图3
★证明直线与圆相切
例2如图4,BC与⊙O相切于点B,AB为⊙O
的直径,弦AD∥OC求证:CD是⊙0的切线
分析:因为直线CD经过半径OD的外端D,所以
只需迸OD⊥CD,这可通过证△COD≌△COB得到
B
图4
例2连接OD
∴AD∥OC,∠COD=∠ODA,∠COB=∠A
OD=OA,∴∠ODA=∠A.
∠COD=∠COB.
又∵OD=OB,OC=OC,
.△COD≌△COB
∠ODC=∠B.
BC与⊙O相切,
∴∠B=90°
∠ODC=90°
CD是⊙O的切线
《变式2》
如图5,在△ABC中,AB=AC,O为底边BC的中
点,⊙O与腰AB相切点D.求证:AC与⊙O相切
B
图5
变式2连接OD,OA,过点O作OE⊥AC于点E
∵AB=AC,OB=OC,∴∠OAB=∠OAC
⊙O与AB相切于点D,OD⊥AB
又∵OE⊥AC,OE=OD.
AC与⊙O相切
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第6课时 直线和圆的位置关系(1)
A自主预习,检测预习效果
(一)学习目标
1.从直线与圆的交点个数理解直线与圆的三种
位置关系,了解割线、切线和切点等概念
2.掌握直线与圆的三种位置关系及相应的数量
关系
3.能运用切线的兴定定理证明直线与圆相切
课前预习
检测1】已知⊙O的半径r=5cm,圆心O到直
线L的距离为d,当d
时
直线L与⊙O有公共点(填写一个
答案即可)
检测2】如图1,A,B是⊙O
上的两点,∠AOB=120°,当∠CAB
B
时,AC是⊙O的切线
图1
参典型问题典例析,名师点拨解媛
★判断直线与圆的位置关系
例1如图2,在△ABC中,BC=2cm,∠B=30°,
∠C=45°.以点A为圆心作⊙A,当半径为多长时,所
作⊙A与直线BC分别有下列位置关系:
(1)相切;
(2)相交;
(3)相离
分析:先列方程求出点A到直线BC的距离,再
根据圆心到直线的距离d与圆的半径r之间的大小
关系确定它们之间的位置关系
B
图2
例1过点A作AD⊥BC于点D.
设AD=x,则BD=V3x,DC=x
于是(√3+1)x=2.解得x=V3-1.
(1)当x=(V3-1)cm时,⊙A与直线BC相切;
(2)当x>(3-1)cm时,⊙A与直线BC相交;
(3)当x<(3-1)cm时,⊙A与直线BC相离
式
如图3,在△ABC中,AB=
AC=5,BC=6.以点C为圆心的
圆与直线AB相切,则此圆的
半径为
图3
★证明直线与圆相切
例2如图4,BC与⊙O相切于点B,AB为⊙O
的直径,弦AD∥OC求证:CD是⊙0的切线
分析:因为直线CD经过半径OD的外端D,所以
只需迸OD⊥CD,这可通过证△COD≌△COB得到
B
图4
例2连接OD
∴AD∥OC,∠COD=∠ODA,∠COB=∠A
OD=OA,∴∠ODA=∠A.
∠COD=∠COB.
又∵OD=OB,OC=OC,
.△COD≌△COB
∠ODC=∠B.
BC与⊙O相切,
∴∠B=90°
∠ODC=90°
CD是⊙O的切线
《变式2》
如图5,在△ABC中,AB=AC,O为底边BC的中
点,⊙O与腰AB相切点D.求证:AC与⊙O相切
B
图5
变式2连接OD,OA,过点O作OE⊥AC于点E
∵AB=AC,OB=OC,∴∠OAB=∠OAC
⊙O与AB相切于点D,OD⊥AB
又∵OE⊥AC,OE=OD.
AC与⊙O相切
同课章节目录
