36第二十四章 直线和圆的位置关系(2)
文档属性
| 名称 | 36第二十四章 直线和圆的位置关系(2) |

|
|
| 格式 | zip | ||
| 文件大小 | 667.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-06 00:00:00 | ||
图片预览






文档简介
(共29张PPT)
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第7课时 直线和圆的位置关系(2)
新课导入自主预习检测预习效果
(一)学习目标
1.掌握切线的性质定理和切线长定理
2.理解切线长、三角形的内切圆、三角形的内心
等概念
3.会求直角三角形内切圆的半径
二)课前预习
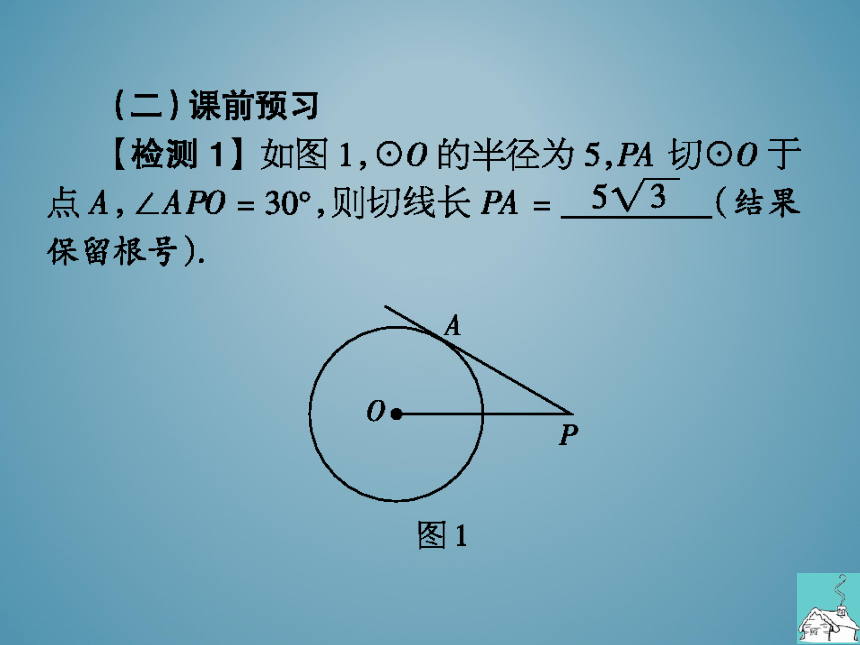
【检测1】如图1,⊙O的半径为5,PA切⊙O于
点A,∠APO=30°,则切线长PA=
(结果
保留根号
P
图1
P
B
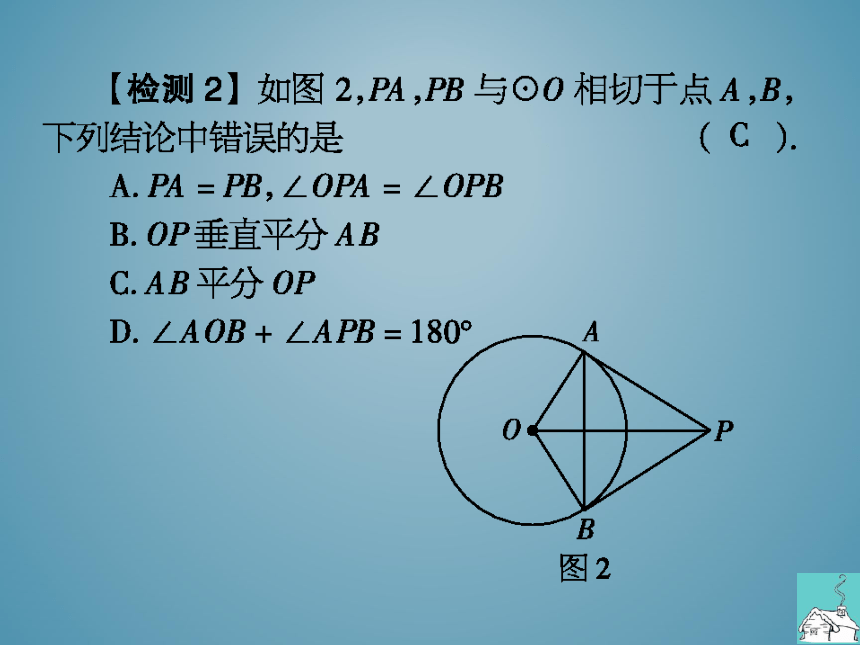
图2
检测2】如图2,PA,PB与⊙0相切于点A,B,
下列结论中错误的是
A.A=PB,∠OmA=∠OPB
B.OP垂直平分AB
C.AB平分OP
D.∠AOB+∠APB=180°
题典例剖析,名师点拨解疑
★切线性质定理的应用
例1如图3,已知AB是⊙O的直径,AC是弦,CD
切⊙0于点C,交AB的延长线于点D,∠ACD=120°,
BD=10
(1)求证:CA=CD;
(2)求⊙O的半径
分析:(1)欲证CA=CD,而∠ACD=120°,因此
需证∠A=30°,而OC=OA,从而需证∠OCA=30°
这可由切线的性质及已知角度而得到.(2)利用含
30°角的直角三角形的性质求解
A
B D
图
例1(1)∵CD切⊙O于点C,∠OCD=90°
∠ACD=120°,∠OCA=30°
∵OC=OA,·∠A=30°,
∠D=30°.∴.CA=CD
(2)设⊙O的半径为r
在Rt△OCD中,由OD=20C得r+10=2.解得r=10
⊙O的半径为10
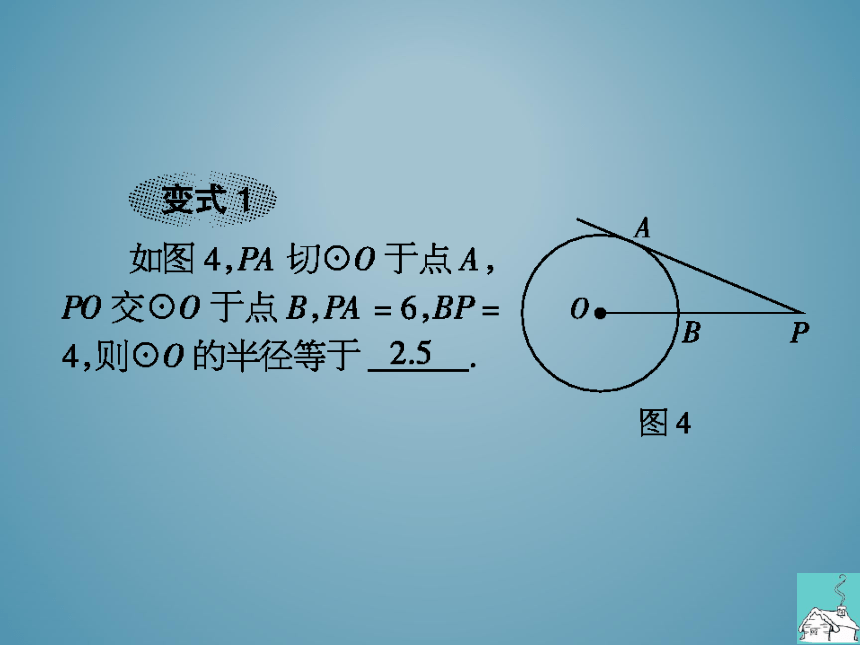
变式腰
如图4,理A切⊙O于点A,
PO交⊙O于点B,PA=6,BP=
4,则O的半径等于
例2如图5,在R△ABC中,∠C=90°,AB
BC=a,CA=b.其内切圆O分别与AB,BC,CA相切
于点D,E,F,⊙O的半径为r求证
(1)四边形OECF是正方形;
(2)r=a+b-c
分析:(1)先证四边形OECF是矩形,再证矩形
OECF是正方形.(2)根据切线长定理求出CE的长
即可
A
E C
图5
例2(1):AC,BC与⊙O相切,
∴∠OFC=∠OEC=90°,
又∵∠C=90°,四边形OECF是矩形.
OE=OF.:矩形OECF是正方形
(2)由切线长定理知AD=AF=b-r,BD=BE=a-r
而AD+BD=c,b-r+a-r=c
r=a+6
2
变式卫除
如图6,△ABC的内切圆分别与BC,CA,AB相
切于点D,E,F.AB=C,BC=a,CA=b,△ABC的面积
为S,⊙的半径为r求证:S=(a+b+c)r
B
D
图6
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第7课时 直线和圆的位置关系(2)
新课导入自主预习检测预习效果
(一)学习目标
1.掌握切线的性质定理和切线长定理
2.理解切线长、三角形的内切圆、三角形的内心
等概念
3.会求直角三角形内切圆的半径
二)课前预习
【检测1】如图1,⊙O的半径为5,PA切⊙O于
点A,∠APO=30°,则切线长PA=
(结果
保留根号
P
图1
P
B
图2
检测2】如图2,PA,PB与⊙0相切于点A,B,
下列结论中错误的是
A.A=PB,∠OmA=∠OPB
B.OP垂直平分AB
C.AB平分OP
D.∠AOB+∠APB=180°
题典例剖析,名师点拨解疑
★切线性质定理的应用
例1如图3,已知AB是⊙O的直径,AC是弦,CD
切⊙0于点C,交AB的延长线于点D,∠ACD=120°,
BD=10
(1)求证:CA=CD;
(2)求⊙O的半径
分析:(1)欲证CA=CD,而∠ACD=120°,因此
需证∠A=30°,而OC=OA,从而需证∠OCA=30°
这可由切线的性质及已知角度而得到.(2)利用含
30°角的直角三角形的性质求解
A
B D
图
例1(1)∵CD切⊙O于点C,∠OCD=90°
∠ACD=120°,∠OCA=30°
∵OC=OA,·∠A=30°,
∠D=30°.∴.CA=CD
(2)设⊙O的半径为r
在Rt△OCD中,由OD=20C得r+10=2.解得r=10
⊙O的半径为10
变式腰
如图4,理A切⊙O于点A,
PO交⊙O于点B,PA=6,BP=
4,则O的半径等于
例2如图5,在R△ABC中,∠C=90°,AB
BC=a,CA=b.其内切圆O分别与AB,BC,CA相切
于点D,E,F,⊙O的半径为r求证
(1)四边形OECF是正方形;
(2)r=a+b-c
分析:(1)先证四边形OECF是矩形,再证矩形
OECF是正方形.(2)根据切线长定理求出CE的长
即可
A
E C
图5
例2(1):AC,BC与⊙O相切,
∴∠OFC=∠OEC=90°,
又∵∠C=90°,四边形OECF是矩形.
OE=OF.:矩形OECF是正方形
(2)由切线长定理知AD=AF=b-r,BD=BE=a-r
而AD+BD=c,b-r+a-r=c
r=a+6
2
变式卫除
如图6,△ABC的内切圆分别与BC,CA,AB相
切于点D,E,F.AB=C,BC=a,CA=b,△ABC的面积
为S,⊙的半径为r求证:S=(a+b+c)r
B
D
图6
同课章节目录
