39第二十四章 正多边形和圆
文档属性
| 名称 | 39第二十四章 正多边形和圆 |

|
|
| 格式 | zip | ||
| 文件大小 | 529.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-06 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第9课时 正多边形和圆
课导A自主预习,检测预习效果
(-)学习目标
1.了解正多边形和圆的有关概念
2.理解并掌握正多边形半径和边长、边心距、中
心角之间的关系,会应用正多边形和圆的有关知识画
正多边形并进行相关计算
(二)课前预习
检测1】下列说法中错误的是
A.各边相等的圆大接多边形是正多边形
B.各角相等的圆内接多边形是正多边形
C.一般地,正n边形的一个内角的度数是
(n-2)·180°
D.正n边形有n条对称轴
检测2】正十边形的中心角是
°,边长为
2cm的正八边形的半径是cm,边长为2√3cm
的正三角形的边心距是cm
③巨典對问圈类倒剖折,名师点被解疑
★正多边形的有关计算
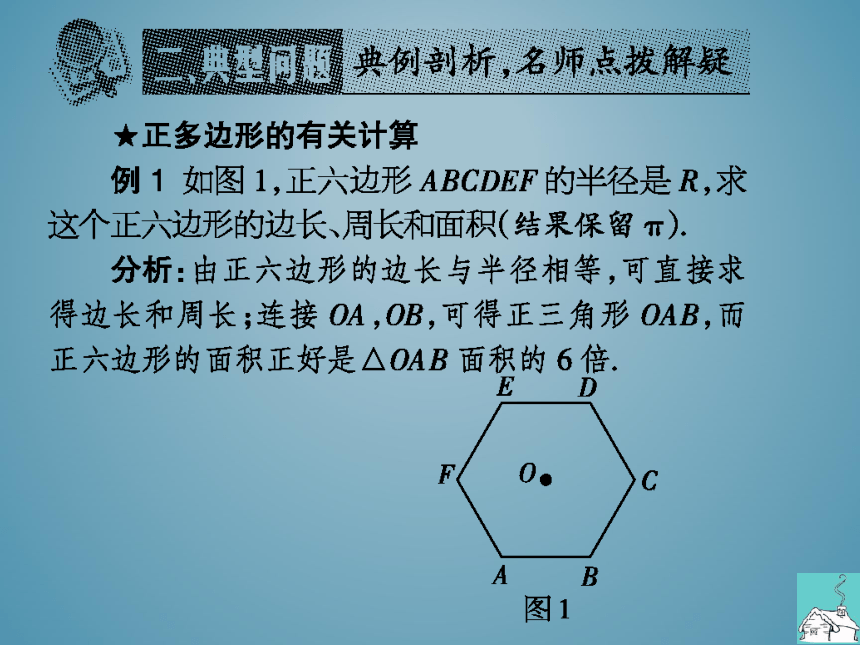
例1如图1,正六边形 ABCDEF的半径是R,求
这个正六边形的边长、周长和面积(结果保留丌)
分析:由正六边形的边长与半径相等,可直接求
得边长和周长;连接OA,OB,可得正三角形OAB,而
正六边形的面积正好是△OAB面积的6倍
菱变式
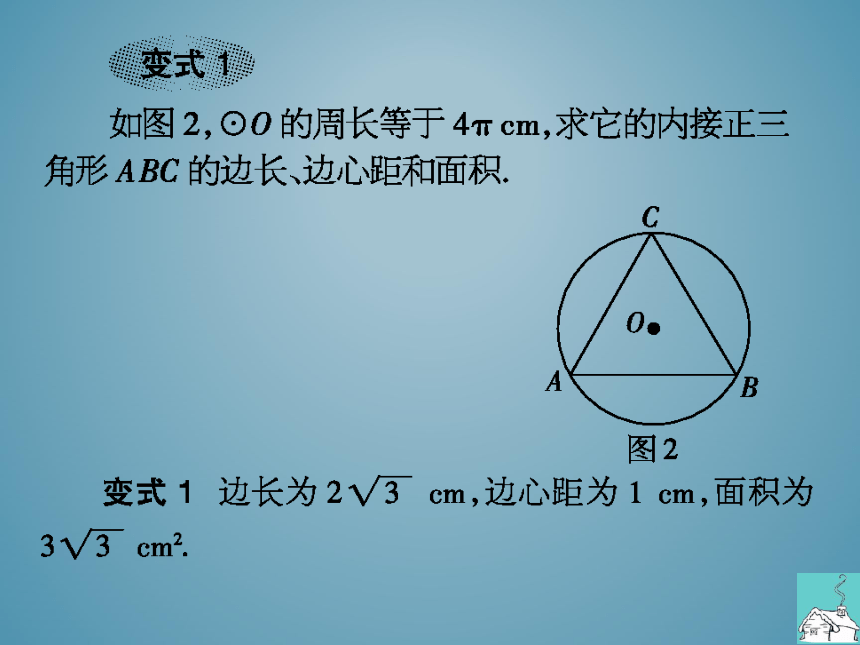
如图2,⊙O的周长等于4Tcm,求它的内接正三
角形ABC的边长边心距和面积
0●
B
图2
变式1边长为2√3cm,边心距为1cm,面积为
3√3cm2
★按要求画正多边形
例2利用等分圆周的方法画一个正八边形
分析:要画正八边形,首先要画一个圆,然后对这
个圆进行八等分,依次连接各个等分点即可
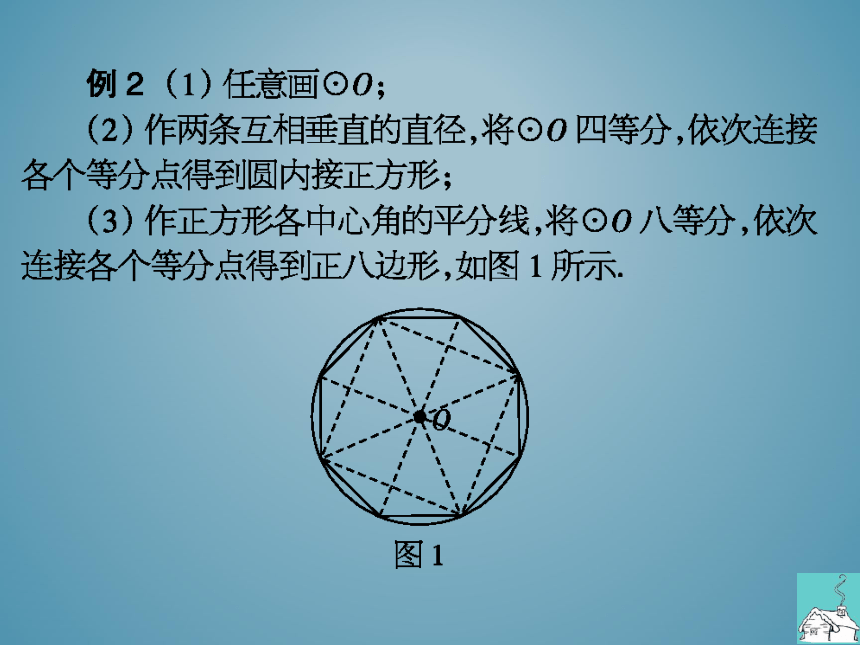
例2(1)任意画⊙O;
(2)作两条互相垂直的直径,将⊙O四等分,依次连接
各个等分点得到圆内接正方形;
(3)作正方形各中心角的平分线,将⊙O八等分,依次
连接各个等分点得到正八边形,如图1所示
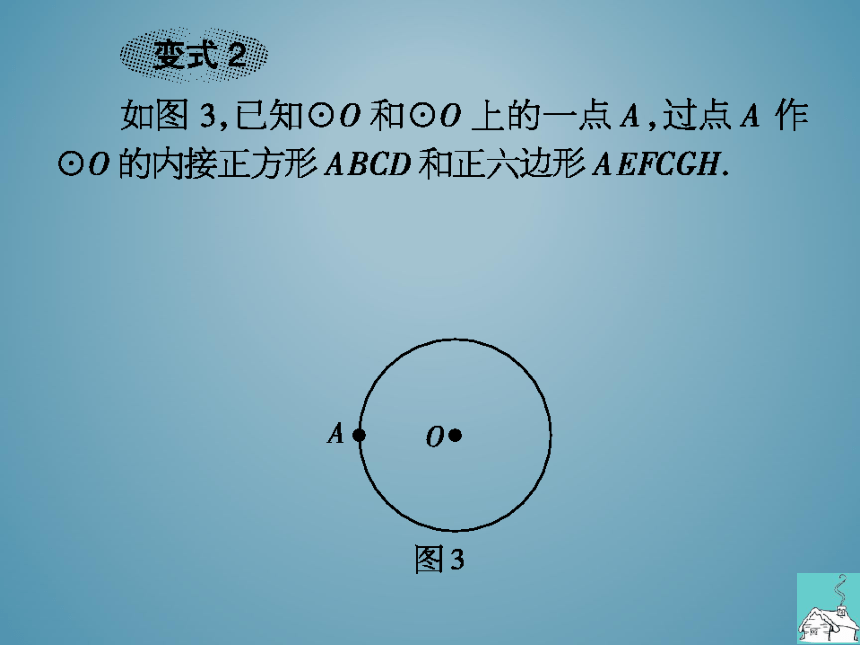
如图3,已知⊙O和⊙O上的一点A,过点A作
⊙O的内接正方形ABCD和正六边形 A EFCGH
图3
D
C
B
图2
三归小结回味反忍,倾悟才能捉高
1.正多边形的
叫做这个
正多边形的中心,
叫做正多边形的
半径,正多边形每一边所对的圆心角叫做正多边形的
二,中心到一边的距离叫做正多边形的
2.如图4,知⊙O的半径是
R,设AB是⊙O内接正n边形的
一边,边长为a,OK是这边的边心
距(长为r),则∠AOB=
K
∠AOK
,R,r和a的关系A
B
是
图4
3.因为圆中相等的圆心角所对的弧
所对的弦也_,所以画正n边形,可以画
度的圆心角,它对着一段弧,然后在圆上依次截取与
这条弧
的弧,就得到圆的个等分点
各分点,即可得出正n边形
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第9课时 正多边形和圆
课导A自主预习,检测预习效果
(-)学习目标
1.了解正多边形和圆的有关概念
2.理解并掌握正多边形半径和边长、边心距、中
心角之间的关系,会应用正多边形和圆的有关知识画
正多边形并进行相关计算
(二)课前预习
检测1】下列说法中错误的是
A.各边相等的圆大接多边形是正多边形
B.各角相等的圆内接多边形是正多边形
C.一般地,正n边形的一个内角的度数是
(n-2)·180°
D.正n边形有n条对称轴
检测2】正十边形的中心角是
°,边长为
2cm的正八边形的半径是cm,边长为2√3cm
的正三角形的边心距是cm
③巨典對问圈类倒剖折,名师点被解疑
★正多边形的有关计算
例1如图1,正六边形 ABCDEF的半径是R,求
这个正六边形的边长、周长和面积(结果保留丌)
分析:由正六边形的边长与半径相等,可直接求
得边长和周长;连接OA,OB,可得正三角形OAB,而
正六边形的面积正好是△OAB面积的6倍
菱变式
如图2,⊙O的周长等于4Tcm,求它的内接正三
角形ABC的边长边心距和面积
0●
B
图2
变式1边长为2√3cm,边心距为1cm,面积为
3√3cm2
★按要求画正多边形
例2利用等分圆周的方法画一个正八边形
分析:要画正八边形,首先要画一个圆,然后对这
个圆进行八等分,依次连接各个等分点即可
例2(1)任意画⊙O;
(2)作两条互相垂直的直径,将⊙O四等分,依次连接
各个等分点得到圆内接正方形;
(3)作正方形各中心角的平分线,将⊙O八等分,依次
连接各个等分点得到正八边形,如图1所示
如图3,已知⊙O和⊙O上的一点A,过点A作
⊙O的内接正方形ABCD和正六边形 A EFCGH
图3
D
C
B
图2
三归小结回味反忍,倾悟才能捉高
1.正多边形的
叫做这个
正多边形的中心,
叫做正多边形的
半径,正多边形每一边所对的圆心角叫做正多边形的
二,中心到一边的距离叫做正多边形的
2.如图4,知⊙O的半径是
R,设AB是⊙O内接正n边形的
一边,边长为a,OK是这边的边心
距(长为r),则∠AOB=
K
∠AOK
,R,r和a的关系A
B
是
图4
3.因为圆中相等的圆心角所对的弧
所对的弦也_,所以画正n边形,可以画
度的圆心角,它对着一段弧,然后在圆上依次截取与
这条弧
的弧,就得到圆的个等分点
各分点,即可得出正n边形
同课章节目录
