74第二十七章 图形的相似
文档属性
| 名称 | 74第二十七章 图形的相似 |

|
|
| 格式 | zip | ||
| 文件大小 | 677.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-06 00:00:00 | ||
图片预览




文档简介
(共27张PPT)
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第1课时 图形的相似
一断课导人自主预习,检测预习效果
(一)学习目标
探索相似图形的性质,能在诸多图形中找出相
似的图形
2.掌握相似多边形的性质和判定方法,并能应用
它们进行简单的计算和证明
(二)课前预习
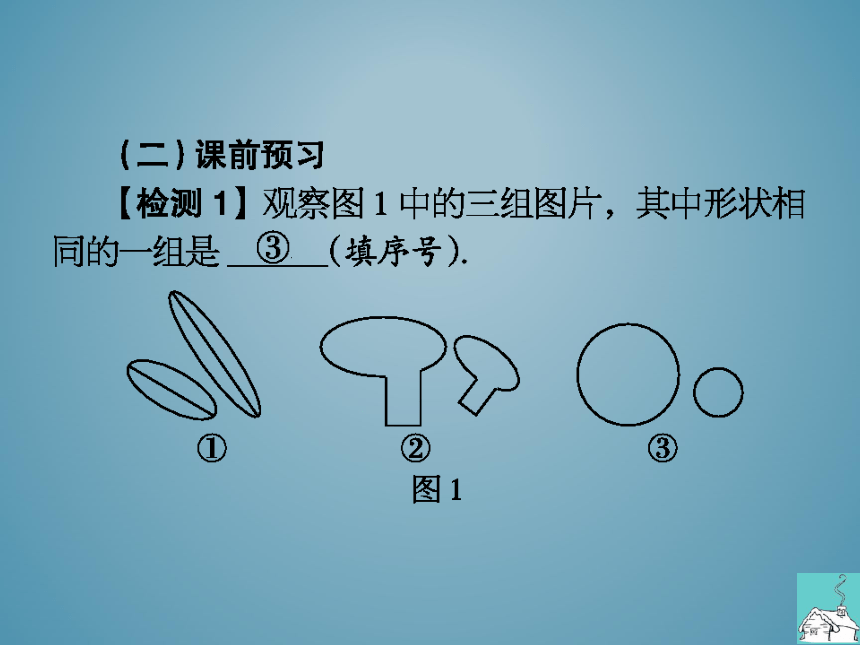
【检测1】观察图1中的三组图片,其中形状相
同的组是
(填序号).
图1
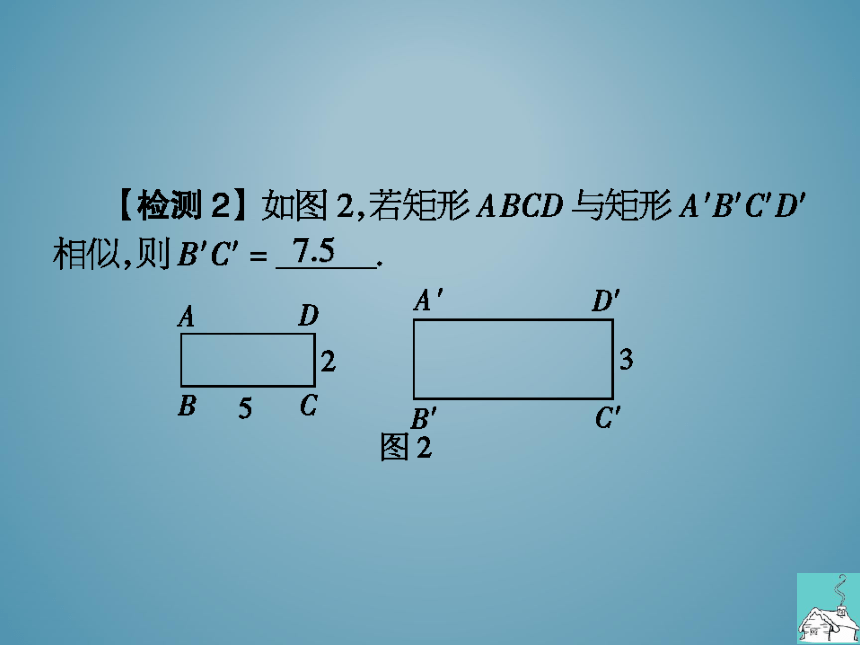
检测2】如图2,若矩形ABCD与矩形ABC"D
相似,则BC
2
B 5 C
B
图2
二典型问题典例剥析名师点拨解疑
★识别相似图形
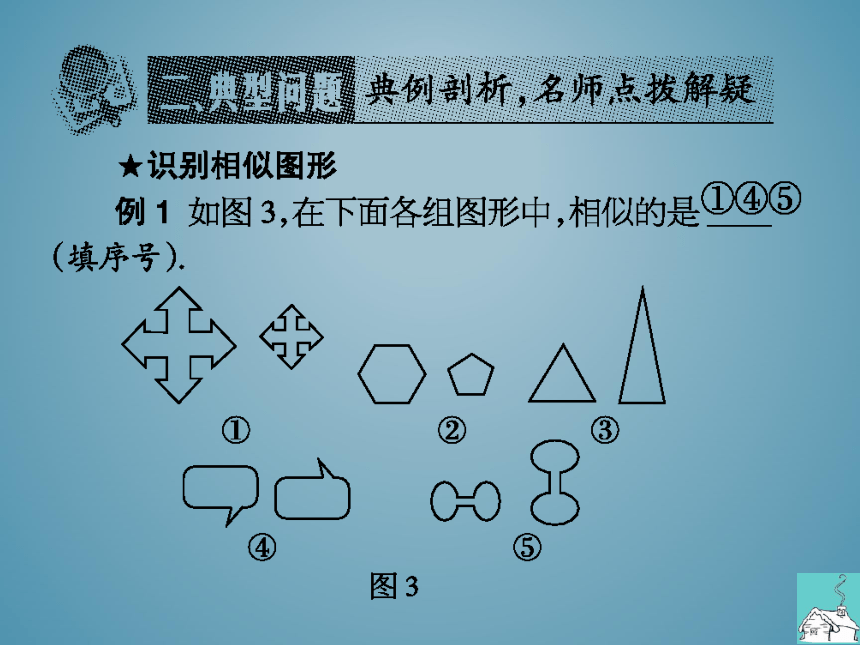
例1如图3,在下面各组图形中,相似的是
(填序号)
◇A
③
图3
分析:找相似图形就是根据相似图形的定义,通过
观察,根据“形状相同”这一特征判断,与图形的大小、
位置无关
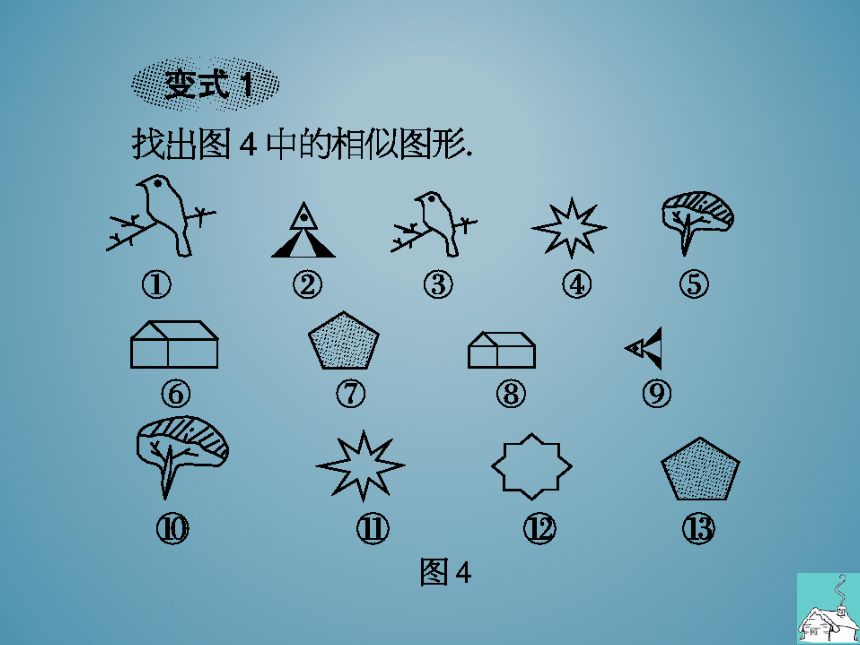
变式
找出图4中的相似图形
A升
③
9+6
图4
变式1①与③,②与⑨,④与①,⑤与⑩,⑥与⑧,
⑦与①
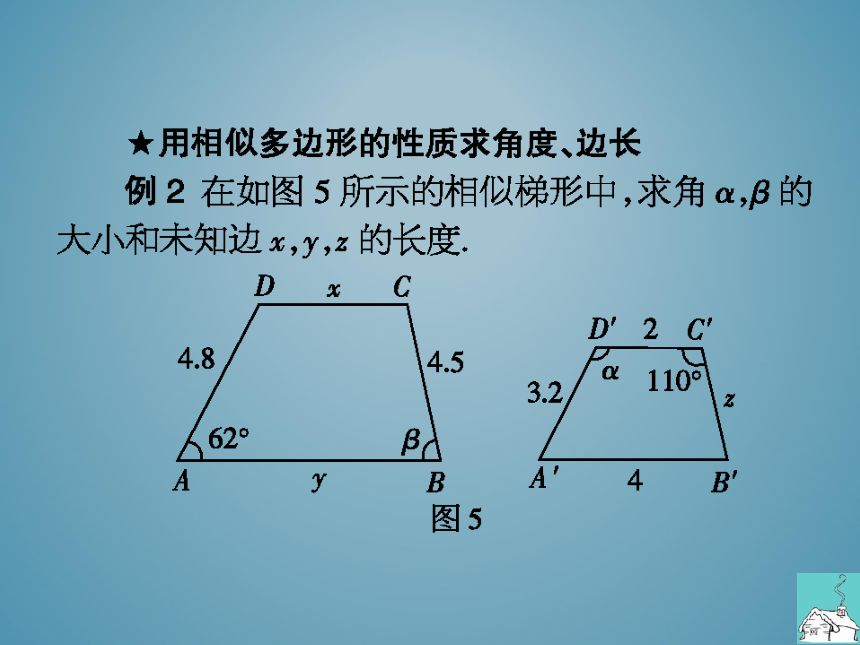
★用相似多边形的性质求角度、边长
例2在如图5所示的相似梯形中,求角a,B的
大小和未知边x,y,z的长度
C
D2 C
4.8
4.5
3.2
10°
62°
β
B
B
图5
分析:先在各梯形中根据梯形的上、下底互相平
行,求出∠D和∠B的度数,再利用相似多边形对应
角相等,对应边的比相等求解
例2由梯形的性质知AB∥CD,A'B'∥C'D',
∴∠D=180°-∠A=180°-62°=118°
∠B=180°-∠C′=180°-110°=70°
梯形ABCD与梯形A'B'CD相似,
∠a=∠D=118°,∠B=∠B=70°
AD
CD
aB
BC
AD′ CD AB B′C
即48==y=45,解得x=3,y=6,z=3
变式2
如图6,△ABC与△DEF相似,求∠B,∠C,∠D,
∠E的大小和未知边x,y的长度
30°
A
4
E
36
D35
B
8
图6
变式2由相似三角形对应角相等,可得∠D=∠A
36°,∠C=∠F=30°,
,∠B=∠E=180-36°-30°=114°
由相似三角形对应边的比相等,可得AB=BC
DE
EF
AC
,即3
812
DF3.5-4
解得x=7,y=6
期鲍小结回咪反思,领悟才能提高
相同的图形叫做相似图形.两个图形
相似,其中一个图形可以看作由另一个图形
得到
2.对于四条线段a,b,c,d,如果
那么线段a,b,c,d是成比例线段,简称比例线段
3.相似多边形对应角,对应边的比
反过来,如果两个多边形满足
相等,
相等,那么这两个多边形相似
4.相似多边形
的比称为相似比.当相
比为1时,两个图形
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第1课时 图形的相似
一断课导人自主预习,检测预习效果
(一)学习目标
探索相似图形的性质,能在诸多图形中找出相
似的图形
2.掌握相似多边形的性质和判定方法,并能应用
它们进行简单的计算和证明
(二)课前预习
【检测1】观察图1中的三组图片,其中形状相
同的组是
(填序号).
图1
检测2】如图2,若矩形ABCD与矩形ABC"D
相似,则BC
2
B 5 C
B
图2
二典型问题典例剥析名师点拨解疑
★识别相似图形
例1如图3,在下面各组图形中,相似的是
(填序号)
◇A
③
图3
分析:找相似图形就是根据相似图形的定义,通过
观察,根据“形状相同”这一特征判断,与图形的大小、
位置无关
变式
找出图4中的相似图形
A升
③
9+6
图4
变式1①与③,②与⑨,④与①,⑤与⑩,⑥与⑧,
⑦与①
★用相似多边形的性质求角度、边长
例2在如图5所示的相似梯形中,求角a,B的
大小和未知边x,y,z的长度
C
D2 C
4.8
4.5
3.2
10°
62°
β
B
B
图5
分析:先在各梯形中根据梯形的上、下底互相平
行,求出∠D和∠B的度数,再利用相似多边形对应
角相等,对应边的比相等求解
例2由梯形的性质知AB∥CD,A'B'∥C'D',
∴∠D=180°-∠A=180°-62°=118°
∠B=180°-∠C′=180°-110°=70°
梯形ABCD与梯形A'B'CD相似,
∠a=∠D=118°,∠B=∠B=70°
AD
CD
aB
BC
AD′ CD AB B′C
即48==y=45,解得x=3,y=6,z=3
变式2
如图6,△ABC与△DEF相似,求∠B,∠C,∠D,
∠E的大小和未知边x,y的长度
30°
A
4
E
36
D35
B
8
图6
变式2由相似三角形对应角相等,可得∠D=∠A
36°,∠C=∠F=30°,
,∠B=∠E=180-36°-30°=114°
由相似三角形对应边的比相等,可得AB=BC
DE
EF
AC
,即3
812
DF3.5-4
解得x=7,y=6
期鲍小结回咪反思,领悟才能提高
相同的图形叫做相似图形.两个图形
相似,其中一个图形可以看作由另一个图形
得到
2.对于四条线段a,b,c,d,如果
那么线段a,b,c,d是成比例线段,简称比例线段
3.相似多边形对应角,对应边的比
反过来,如果两个多边形满足
相等,
相等,那么这两个多边形相似
4.相似多边形
的比称为相似比.当相
比为1时,两个图形
