75第二十七章 相似三角形的判定(1)
文档属性
| 名称 | 75第二十七章 相似三角形的判定(1) |  | |
| 格式 | zip | ||
| 文件大小 | 589.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-06 18:47:11 | ||
图片预览






文档简介
(共25张PPT)
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第2课时 相似三角形的判定(1)
c□新课导入自主预习检测预习放果
(一)学习目标
1.理解相似三角形的概念,并会用以证明和计算.
2.体会用相似符号“∽”表示的相似三角形之间
的边、角对应关系
3.了解平行线分线段成比例定理及其推论,会用
平行线证明两个三角形相似,并从中建立相等的比,
用以证明、计算
(二)课前预习
【检测1】已知△ABC∽△ABC,相秘为3:5,
且∠A=60°,∠B=36°,则△A'B'C与△ABC的相似
比为
检测2】如图1,在△ABC中,
DE∥BC,则△
△
对应边的比为AD
E
aB
B
心巨典型洞题典例剖析,名师点拨解疑
★相似三角形中的边、角对应关系
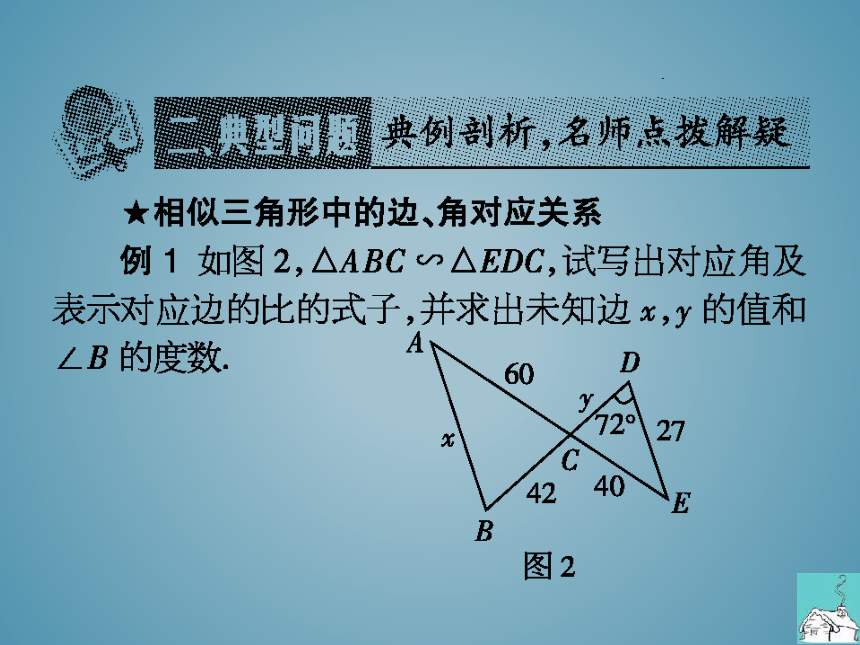
例1如图2,△ABC∽△EDC,试写出对应角及
表示对应边的比的式子,并求出未知边x,y的值和
∠B的度数
A
60
7227
4240
E
B
图2
分析:当两个相似三角形用符号“∽”表示时,对
应顶点已经给出,即相应位置上的点是对应点,由对
应点可以写出对应角、对应边,再由相似三角形的性
质写出表示对应边的比的式子,进而求出x,y的值和
∠B的度数
例1∠A与∠E,∠B与∠D,∠ACB与∠ECD是对应
角;表示对应边的比的式子是AB=BC=AC
ED
DC
EC
∠B=72°
4260
40
解得x=40.5,y=28
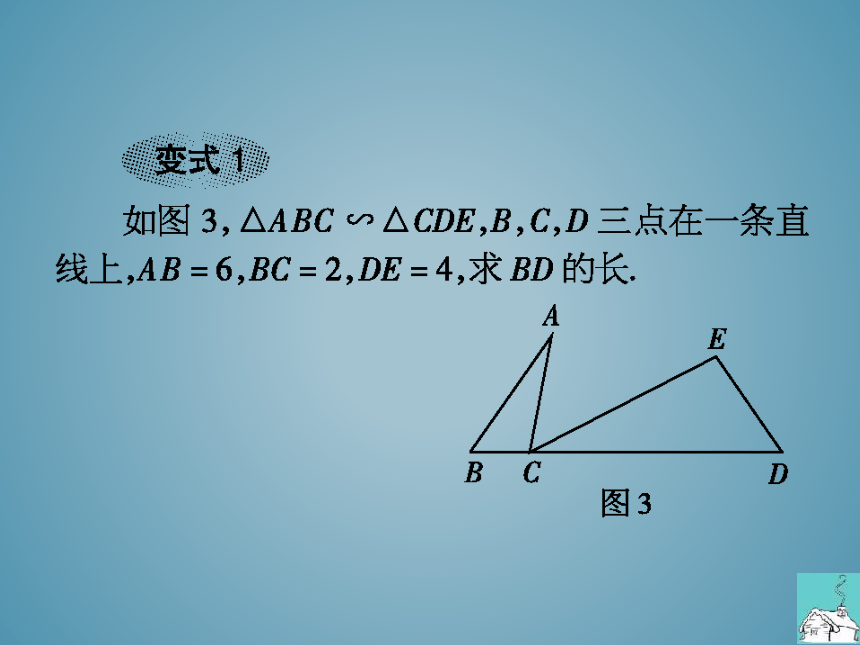
变式1影
如图3,△ABC∽△CDE,B,C,D三点在一条直
线上,AB=6,BC=2,DE=4,求BD的长
B C
D
图3
变式1∵△ABC∽△CDE,AB=BC
CD
DE
解得CD=12.∴BD=BC+CD=2+12=14.
4
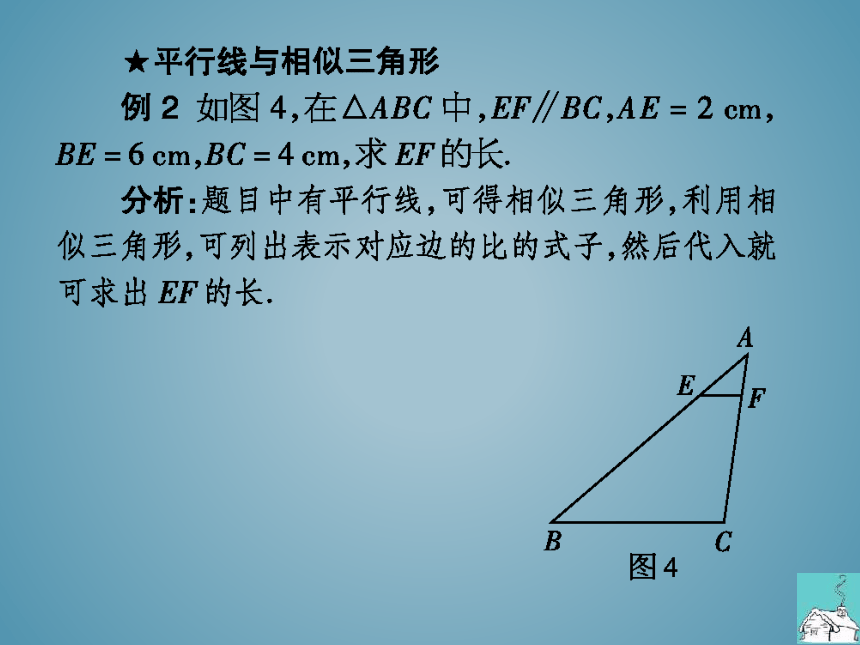
★平行线与相似三角形
例2如图4,在△ABC中,EF∥BC,AE=2cm
BE=6cm,BC=4cm,求EF的长
分析:题目中有平行线,可得相似三角形,利用相
似三角形,可列出表示对应达的比的式子,然后代入就
可求出EF的长
E
F
B
C
图4
例2∵EF∥BC,△AEF∽△ABC,AE_EF
AB BC
E
EF
cm
2+6
4
变式2
如图5,在□ABCD中,EF∥AB,DE:EA=2:3,
EF=4,求CD的长
B
图5
变式2∵DE:EA=2:3,DE:DA=2:5
EF∥AB,∴△DEF∽△DAB
DE -EF Rn 2
DA AB
即
4
AB
解得AB=10.
又∵四边形ABCD是平行四边形,CD=AB=10
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第2课时 相似三角形的判定(1)
c□新课导入自主预习检测预习放果
(一)学习目标
1.理解相似三角形的概念,并会用以证明和计算.
2.体会用相似符号“∽”表示的相似三角形之间
的边、角对应关系
3.了解平行线分线段成比例定理及其推论,会用
平行线证明两个三角形相似,并从中建立相等的比,
用以证明、计算
(二)课前预习
【检测1】已知△ABC∽△ABC,相秘为3:5,
且∠A=60°,∠B=36°,则△A'B'C与△ABC的相似
比为
检测2】如图1,在△ABC中,
DE∥BC,则△
△
对应边的比为AD
E
aB
B
心巨典型洞题典例剖析,名师点拨解疑
★相似三角形中的边、角对应关系
例1如图2,△ABC∽△EDC,试写出对应角及
表示对应边的比的式子,并求出未知边x,y的值和
∠B的度数
A
60
7227
4240
E
B
图2
分析:当两个相似三角形用符号“∽”表示时,对
应顶点已经给出,即相应位置上的点是对应点,由对
应点可以写出对应角、对应边,再由相似三角形的性
质写出表示对应边的比的式子,进而求出x,y的值和
∠B的度数
例1∠A与∠E,∠B与∠D,∠ACB与∠ECD是对应
角;表示对应边的比的式子是AB=BC=AC
ED
DC
EC
∠B=72°
4260
40
解得x=40.5,y=28
变式1影
如图3,△ABC∽△CDE,B,C,D三点在一条直
线上,AB=6,BC=2,DE=4,求BD的长
B C
D
图3
变式1∵△ABC∽△CDE,AB=BC
CD
DE
解得CD=12.∴BD=BC+CD=2+12=14.
4
★平行线与相似三角形
例2如图4,在△ABC中,EF∥BC,AE=2cm
BE=6cm,BC=4cm,求EF的长
分析:题目中有平行线,可得相似三角形,利用相
似三角形,可列出表示对应达的比的式子,然后代入就
可求出EF的长
E
F
B
C
图4
例2∵EF∥BC,△AEF∽△ABC,AE_EF
AB BC
E
EF
cm
2+6
4
变式2
如图5,在□ABCD中,EF∥AB,DE:EA=2:3,
EF=4,求CD的长
B
图5
变式2∵DE:EA=2:3,DE:DA=2:5
EF∥AB,∴△DEF∽△DAB
DE -EF Rn 2
DA AB
即
4
AB
解得AB=10.
又∵四边形ABCD是平行四边形,CD=AB=10
