77第二十七章 相似三角形的判定(3)
文档属性
| 名称 | 77第二十七章 相似三角形的判定(3) |

|
|
| 格式 | zip | ||
| 文件大小 | 610.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-06 00:00:00 | ||
图片预览




文档简介
(共27张PPT)
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第4课时 相似三角形的判定(3)
-谍导入自主预习,检测预习效果
(一)学习目标
1.掌握相似三角形的判定方法:两角对应相等的
两个三角形相似
2.能灵活选择相似三角形的三个判定定理,证明
两个三角形相似并解决有关问题
3.进一步体会代数方法及分类讨论的数学思想
在相似三角形学习中的应用价值
(二)课前预习
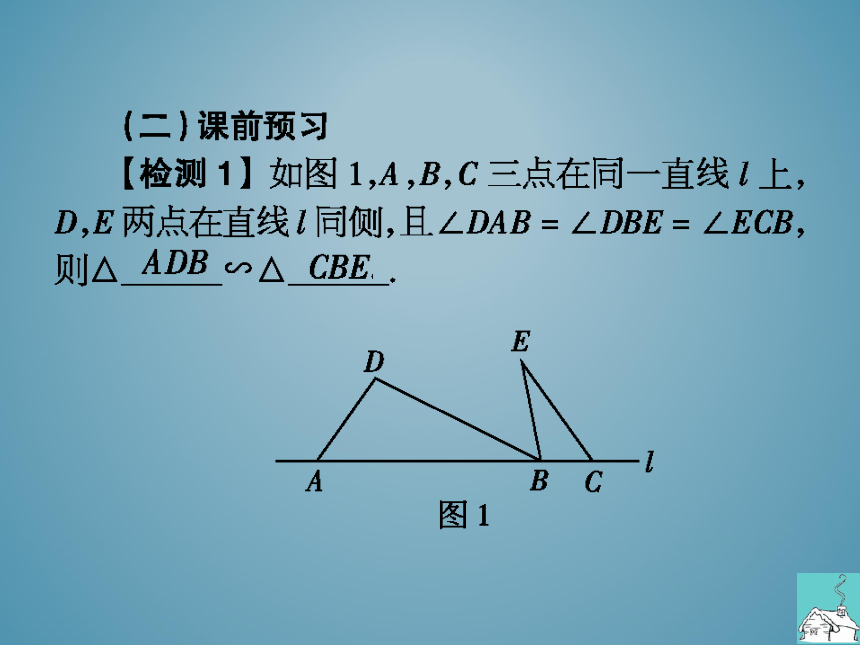
检测1】如图1,A,B,C三点在同一直线L上,
D,E两点在直线L同侧,且∠DAB=∠DBE=∠ECB,
则△
∽△
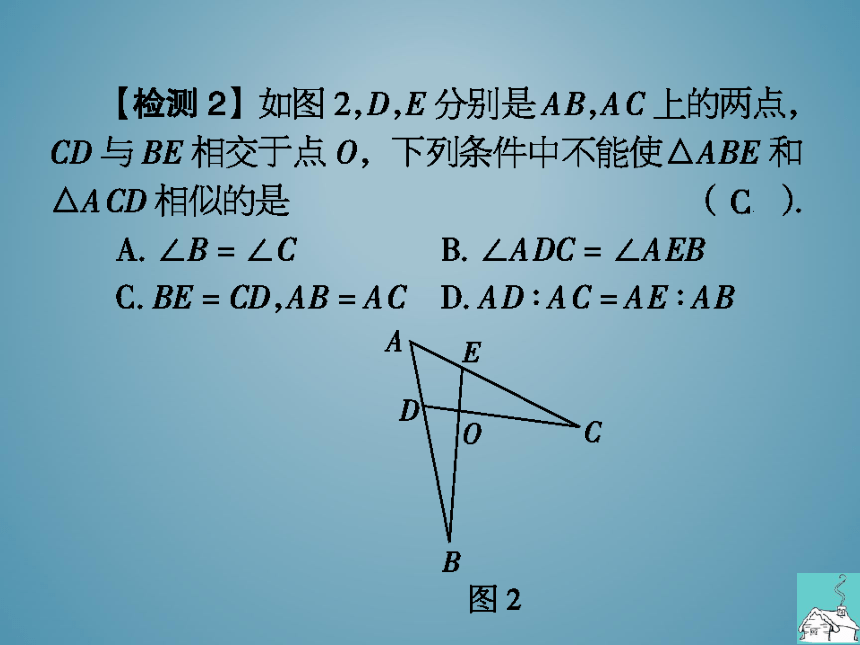
检测2】如图2,D,E分别是AB,AC上的两点,
CD与BE相交于点O,下列条件中不能使△ABE和
△ACD相似的是
A.∠B=∠C
B.∠ADC=∠AEB
C BE= CD.AB=AC D AD:AC=AE: AB
最例剖析,名师点拨解疑
★判定三角形相似
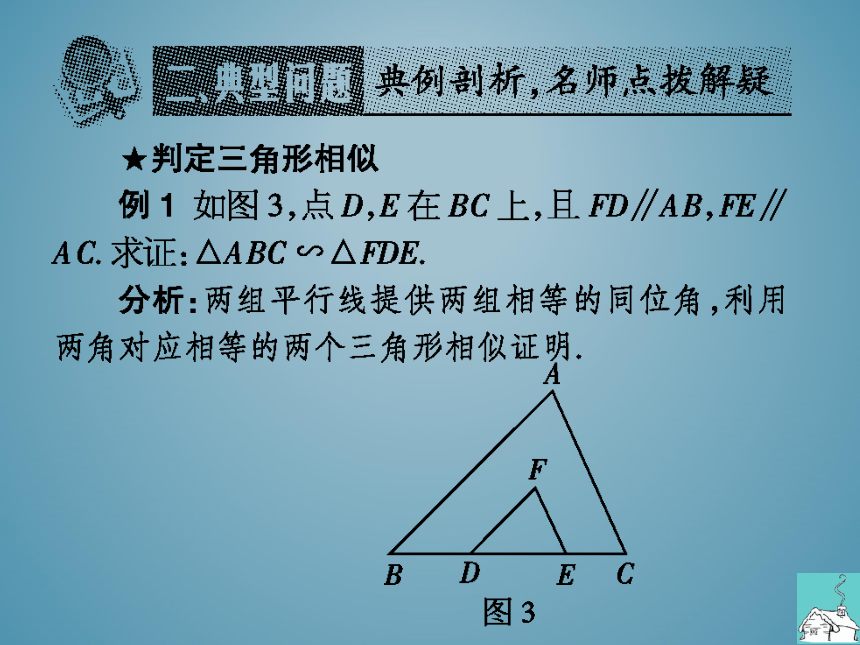
例1如图3,点D,E在BC上,且FD∥AB,E∥
AC求证:△ABC∽△FDE
分析:两组平行线提供两组相等的同位角,利用
两角对应相等的两个三角形相似证明
例1PD∥AB,;∠B=∠DE
∵∥AC,∠C=∠FD.∴△ABC∽△FDE
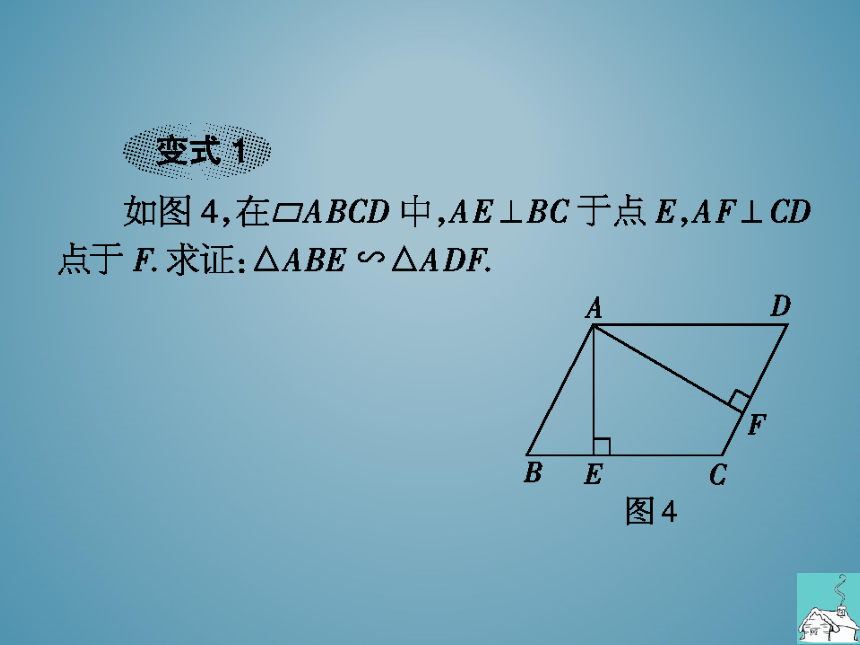
变式
如图4,在□ABCD中,AE⊥BC于点E,AF⊥CD
点于F.求证:△ABE∽△ADF
B E
图4
变式1:AE⊥BC,AF⊥CD,∠AEB=∠APD=90°
∴四边形ABCD是平行四边形,
,∠B=∠D.∴△ABE∽△ADF
★证明等积式
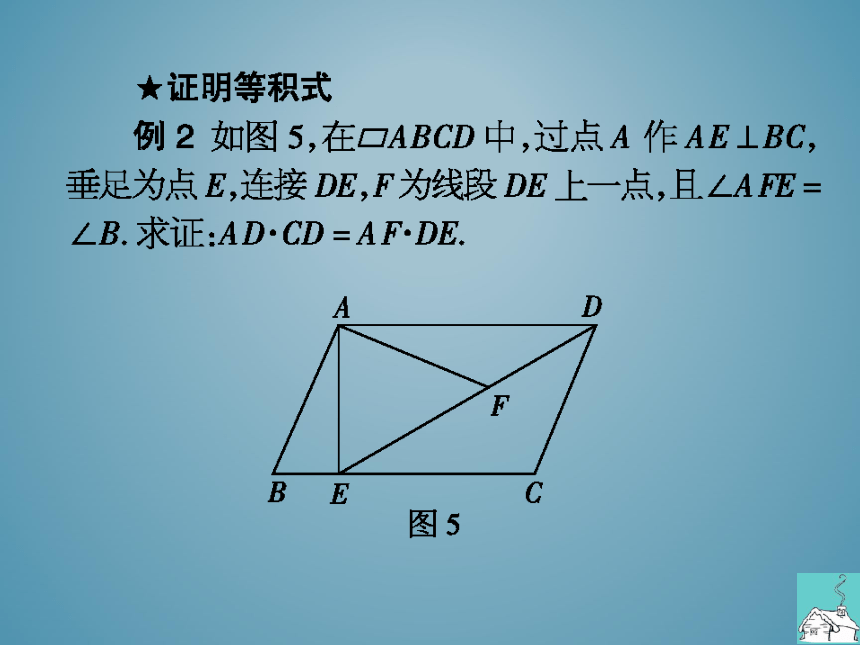
例2如图5,在□ABCD中,过点A作AE⊥BC,
垂足为点E连接DE,F为线段DE上一点,且∠AF=
∠B.求证:ADCD=AFDE
D
B E
C
图5
分析:大多数等积式的证明问题都与相似三角形
有关.先将等积式转化为表示等比的式子,如将AD
CD=AFDE转化为4D=AF,再寻求条件证明
DE
CD
△ADF与△DEC相似
∴∠ADF=∠CED,∠B+∠C=180°
∵∠A配+∠AFD=180°,∠AFE=∠B,
∠AF=∠C.
∴△ADF∽△DEC.∴,AD-AF
DE CD
即ADCD=AF·DE.
式
如图6,CD是Rt△ACB斜边上的高,点E为AC
的中点,ED交CB的延长线于点F
求证:BDCF=CDDF
B
D
F
图6
变式2:CD⊥AB,点E为AC的中点,
.DE=AE.∴,∠EDA=∠A.
∵∠EDA=∠FDB,,∠A=∠FDB
∵∠ACD+∠FCD=∠ACD+∠A=90°,
∠A=∠FCD.∴∵.∠PDB=∠FCD
又∵∠F=∠F,△FDB∽△FCD,
BD DE
BD·CF=CD·DF
CD CF
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第4课时 相似三角形的判定(3)
-谍导入自主预习,检测预习效果
(一)学习目标
1.掌握相似三角形的判定方法:两角对应相等的
两个三角形相似
2.能灵活选择相似三角形的三个判定定理,证明
两个三角形相似并解决有关问题
3.进一步体会代数方法及分类讨论的数学思想
在相似三角形学习中的应用价值
(二)课前预习
检测1】如图1,A,B,C三点在同一直线L上,
D,E两点在直线L同侧,且∠DAB=∠DBE=∠ECB,
则△
∽△
检测2】如图2,D,E分别是AB,AC上的两点,
CD与BE相交于点O,下列条件中不能使△ABE和
△ACD相似的是
A.∠B=∠C
B.∠ADC=∠AEB
C BE= CD.AB=AC D AD:AC=AE: AB
最例剖析,名师点拨解疑
★判定三角形相似
例1如图3,点D,E在BC上,且FD∥AB,E∥
AC求证:△ABC∽△FDE
分析:两组平行线提供两组相等的同位角,利用
两角对应相等的两个三角形相似证明
例1PD∥AB,;∠B=∠DE
∵∥AC,∠C=∠FD.∴△ABC∽△FDE
变式
如图4,在□ABCD中,AE⊥BC于点E,AF⊥CD
点于F.求证:△ABE∽△ADF
B E
图4
变式1:AE⊥BC,AF⊥CD,∠AEB=∠APD=90°
∴四边形ABCD是平行四边形,
,∠B=∠D.∴△ABE∽△ADF
★证明等积式
例2如图5,在□ABCD中,过点A作AE⊥BC,
垂足为点E连接DE,F为线段DE上一点,且∠AF=
∠B.求证:ADCD=AFDE
D
B E
C
图5
分析:大多数等积式的证明问题都与相似三角形
有关.先将等积式转化为表示等比的式子,如将AD
CD=AFDE转化为4D=AF,再寻求条件证明
DE
CD
△ADF与△DEC相似
∴∠ADF=∠CED,∠B+∠C=180°
∵∠A配+∠AFD=180°,∠AFE=∠B,
∠AF=∠C.
∴△ADF∽△DEC.∴,AD-AF
DE CD
即ADCD=AF·DE.
式
如图6,CD是Rt△ACB斜边上的高,点E为AC
的中点,ED交CB的延长线于点F
求证:BDCF=CDDF
B
D
F
图6
变式2:CD⊥AB,点E为AC的中点,
.DE=AE.∴,∠EDA=∠A.
∵∠EDA=∠FDB,,∠A=∠FDB
∵∠ACD+∠FCD=∠ACD+∠A=90°,
∠A=∠FCD.∴∵.∠PDB=∠FCD
又∵∠F=∠F,△FDB∽△FCD,
BD DE
BD·CF=CD·DF
CD CF
