81第二十七章 位似(2)
文档属性
| 名称 | 81第二十七章 位似(2) |

|
|
| 格式 | zip | ||
| 文件大小 | 823.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-06 00:00:00 | ||
图片预览






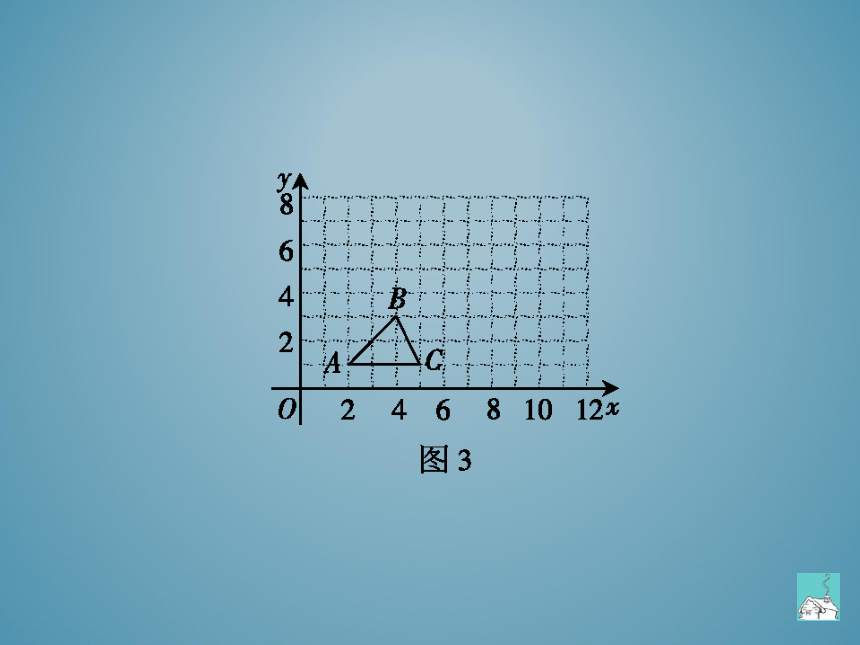
文档简介
(共28张PPT)
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第8课时 位似(2)
新谋导人白主预习检测预习效果
(一)学习目标
1.巩固位似图形及其有关概念
2.会用图形的坐标的变化来表示图形的位似变
换,掌握把个图形按定大小比例放大或缩小后,
点的巫标的娈化规律
(二)课前预习
检测1)线段AB的端点坐标分别为A(6,3),
B(4,-2),以原点O为位似中心、相似比为把
线段AB缩小,点A,B的对应点的坐标分别为
A'O
B′(
)(写出一种情况即可
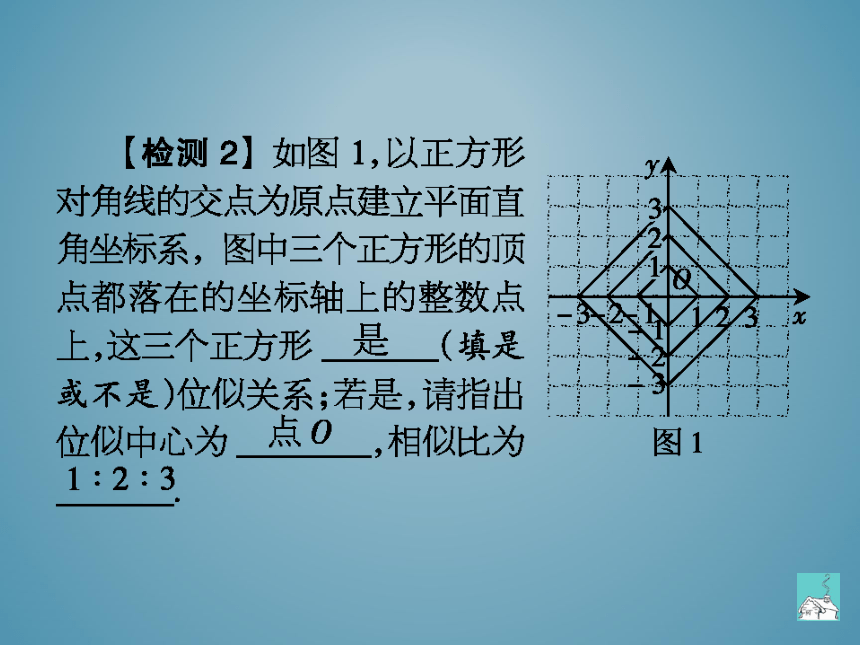
检测2】如图1,以正方形
y
对角线的交点为原点建立平面直
角坐标系,图中三个正方形的顶
点都落在的坐标轴上的整数点
上,这三个正方形
(填是
或不是)位似关系;若是,请指出
位似中心为
,相似比为
图1
典型同題典例剃折,名师点拨解疑
★以原点为位似中心
例1如图2,△AOB缩小后得到△COD,观察变
化前后的三角形顶点,它们的坐标发生了什么变化,
并求出△AOB与△COD的相似此和面积比
分析:根据已知点A,C的坐标可得两个三角形的
相似比,然后根据相似比得到其他坐标的变化和面积比
B
2
6
C4
2
2
图
2
例1由图知A(-5,0),C(-3,0),故△AOB与△COD
的相似此为 ,△COD顶点的横、纵坐标都变为△AOB的
的3,△AOB与△COD的面积比为
25
9
变式1
已知△ABC的三个页点坐标如下表:
(2x,2y)
A(2,1)
A'(4,2)
B(4,3)
BO
C(5,1)
C(,)
(1)将表补充完整,并在如图3所示的平面直角
巫标系中画出△AB'C';
(2)观察△ABC与△AB'C′,写出有关这两个三
角形关系的一个正确结论
y864
:
B
s!!
;”…、
O24681012x
3
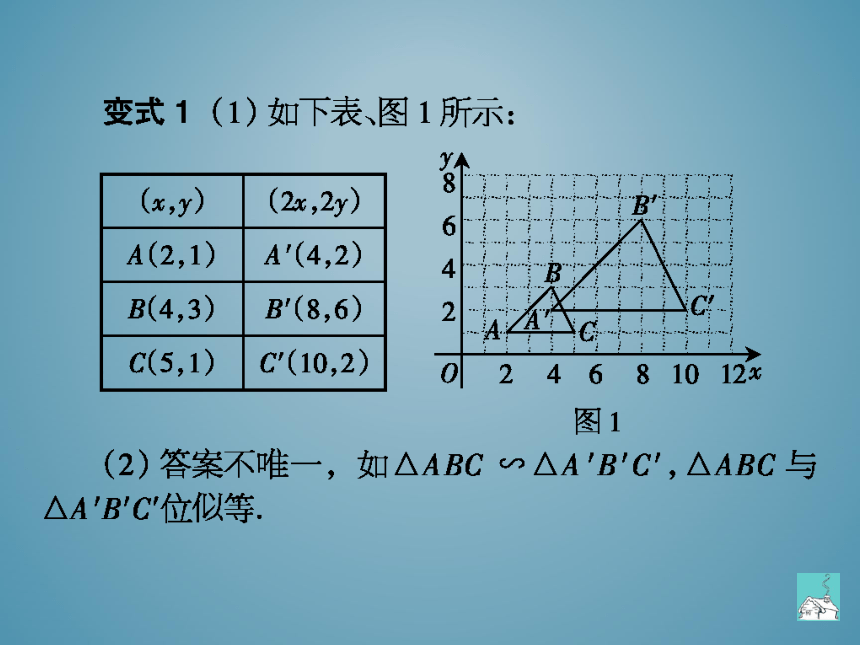
变式1(1)如下表图1所示:
(x,y)(2x,2y)
A(2,1)A(4,2)
y8642
B(4,3)B(8,6)
C(5,1)c(10,2)
024681012x
图1
(2)答案不唯一,如△ABC∽△A'B'C',△ABC与
△ABC位似等
★以非原点的点为位似中心
例2如图4,在12×12的正方形网格中,△mAB
的顶页点坐标分别为T1,1),A(2,3),B(4,2)
(1)以点r1,1)为位似中心,按比例尺(A:mA)
3:1在位似中心的同侧将△AB放大为△AB′,放
大后点A,B的对应点分别为A',B'.画出△TA'B,并
写出点A',B的坐标
(2)在(1)中,若C(a,b)为线段AB上任一点,写
出变化后点C的对应点C的巫标
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第8课时 位似(2)
新谋导人白主预习检测预习效果
(一)学习目标
1.巩固位似图形及其有关概念
2.会用图形的坐标的变化来表示图形的位似变
换,掌握把个图形按定大小比例放大或缩小后,
点的巫标的娈化规律
(二)课前预习
检测1)线段AB的端点坐标分别为A(6,3),
B(4,-2),以原点O为位似中心、相似比为把
线段AB缩小,点A,B的对应点的坐标分别为
A'O
B′(
)(写出一种情况即可
检测2】如图1,以正方形
y
对角线的交点为原点建立平面直
角坐标系,图中三个正方形的顶
点都落在的坐标轴上的整数点
上,这三个正方形
(填是
或不是)位似关系;若是,请指出
位似中心为
,相似比为
图1
典型同題典例剃折,名师点拨解疑
★以原点为位似中心
例1如图2,△AOB缩小后得到△COD,观察变
化前后的三角形顶点,它们的坐标发生了什么变化,
并求出△AOB与△COD的相似此和面积比
分析:根据已知点A,C的坐标可得两个三角形的
相似比,然后根据相似比得到其他坐标的变化和面积比
B
2
6
C4
2
2
图
2
例1由图知A(-5,0),C(-3,0),故△AOB与△COD
的相似此为 ,△COD顶点的横、纵坐标都变为△AOB的
的3,△AOB与△COD的面积比为
25
9
变式1
已知△ABC的三个页点坐标如下表:
(2x,2y)
A(2,1)
A'(4,2)
B(4,3)
BO
C(5,1)
C(,)
(1)将表补充完整,并在如图3所示的平面直角
巫标系中画出△AB'C';
(2)观察△ABC与△AB'C′,写出有关这两个三
角形关系的一个正确结论
y864
:
B
s!!
;”…、
O24681012x
3
变式1(1)如下表图1所示:
(x,y)(2x,2y)
A(2,1)A(4,2)
y8642
B(4,3)B(8,6)
C(5,1)c(10,2)
024681012x
图1
(2)答案不唯一,如△ABC∽△A'B'C',△ABC与
△ABC位似等
★以非原点的点为位似中心
例2如图4,在12×12的正方形网格中,△mAB
的顶页点坐标分别为T1,1),A(2,3),B(4,2)
(1)以点r1,1)为位似中心,按比例尺(A:mA)
3:1在位似中心的同侧将△AB放大为△AB′,放
大后点A,B的对应点分别为A',B'.画出△TA'B,并
写出点A',B的坐标
(2)在(1)中,若C(a,b)为线段AB上任一点,写
出变化后点C的对应点C的巫标
