88第二十八章 锐角三角函数(1)
文档属性
| 名称 | 88第二十八章 锐角三角函数(1) |

|
|
| 格式 | zip | ||
| 文件大小 | 464.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-06 18:47:11 | ||
图片预览






文档简介
(共21张PPT)
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第1课时 锐角三角函数(1)
课导人自主预习,检测预习效果
(一)学习目标
1.理解在直角三角形中,当锐角固定时,它的对
边与斜边的比是个固定值的事实
2.掌握正弦的概念,在直角三角形中,会求一个
锐角的正弦值.
二)课前预习
【检测1】下列命题:①sina表示角a与符号sin
的乘积②在△ABC中,若∠C=90°,则sinA
AB
BC
成立;③已知α为锐角,sina表示的是个比值.其
中真命题有
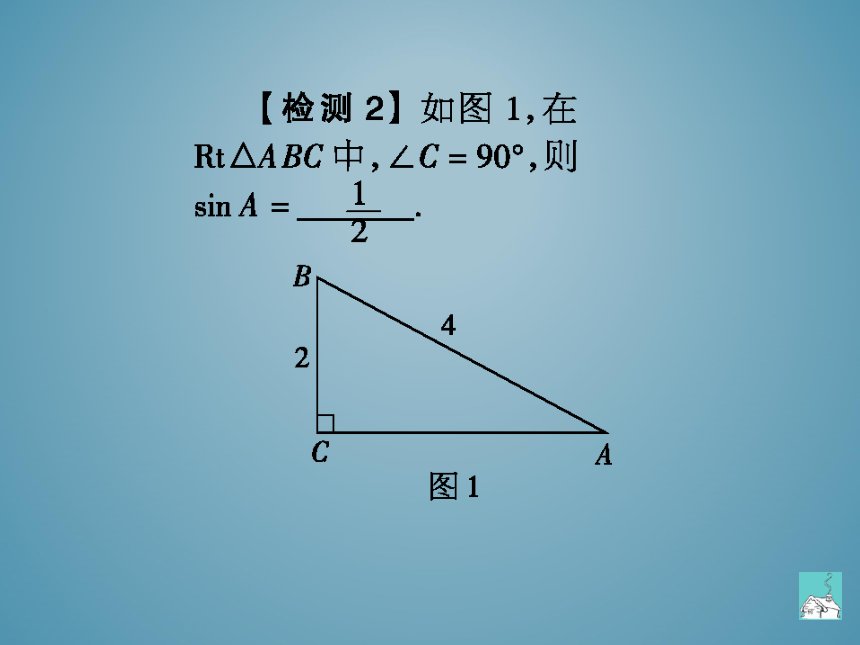
【检测2】如图1,在
R△ABC中,∠C=90°,贝
SInA=
典回澳例剥祈,名师点拨疑
★直接求锐角的正弦值
例1如图2,在△ABC中,∠ACB=90°,AC=4
BC=3,求sinA,sinB的值
分析:根据勾股定理易求出斜边AC的长,再根
据正弦的定义求sinA,sinB的值即可
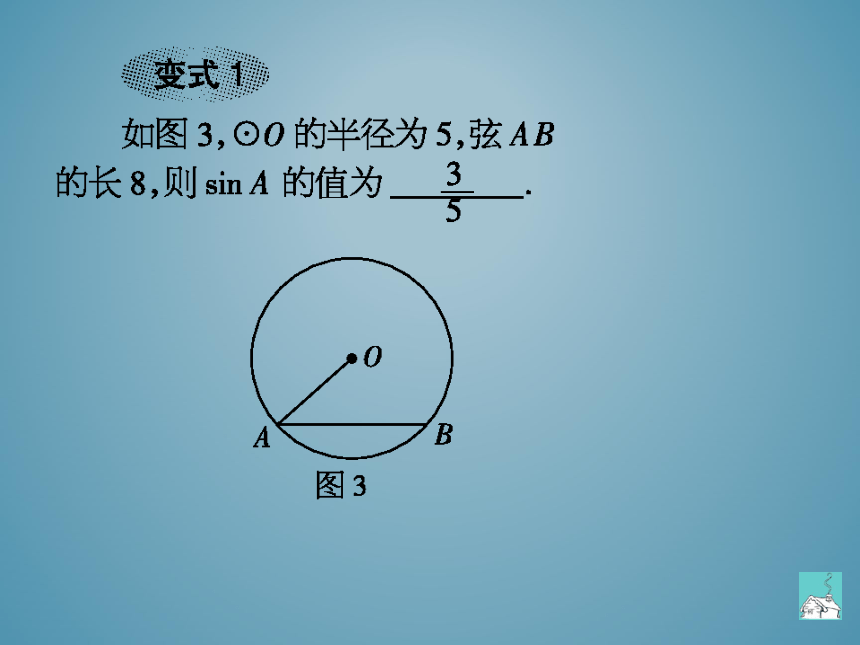
变式
如图3,○O的半径为5,弦AB
的长8,则sinA的值为
例2在Rt△ABC中,∠C=909,AC=BC,求sinA
的值.
分析:由题意可知,△ABC为等腰直角三角形,所
以AC:BC:AB=1:1:V2,再根据正弦的定义即
可得出sinA的值
变式22
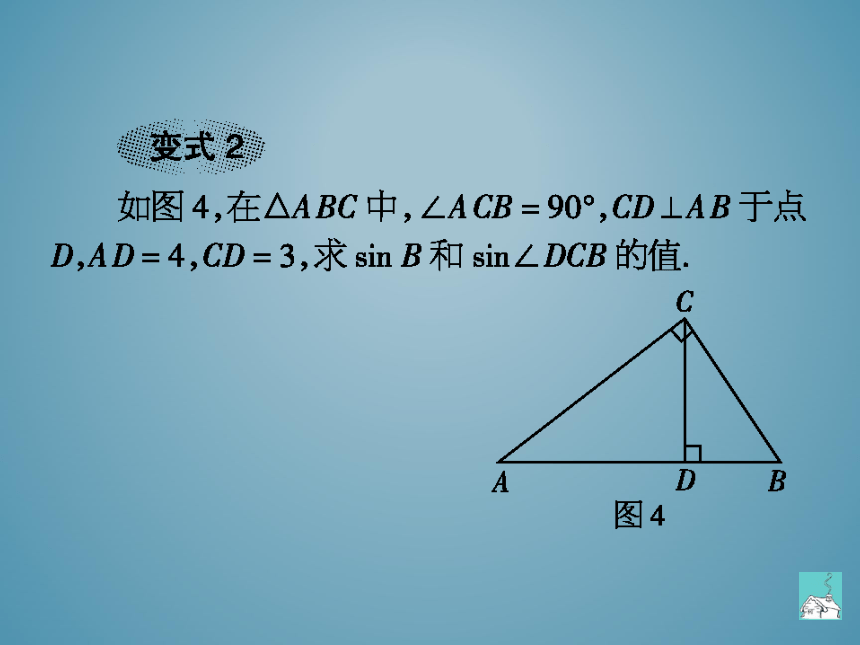
如图4,在△ABC中,∠ACB=90°,CD⊥AB于点
D,AD=4,CD=3,求sinB和sin∠DCB的值
B
图4
变式2snB=sin∠ACD=4
S,sin∠DCB=sinA
回味反思,领悟才能提
1.在直角三角形中,当锐角A的度数一定时,不
管三角形的大小如何,∠A的对边与斜边的比都是
2.在R△ABC中,∠C=90°,AB=C,BC=a,把
锐角A的
与的比叫做∠A的正弦,记
作
即sinA
3.正弦是在直角三角形中定义的,其本质是两条
线段的比值,是一个数值,没有单位,其大小只与锐角
的大小有关,而与锐角所在直角三角形的大小无关.
四除档训练自主练兵,会做才算懂了
A组:基础练习
1.在Rt△ABC中,∠C=90°,若将各边长度都扩
大为原来的4倍,则∠A的正弦值
().
A.扩大4倍
B.缩小4倍
C.扩大2倍
D.不变
2.在△ABC中,AC=8,BC=6,AB=10,则sinA
的值为
().
A
B.4
5
D
534
3.在Rt△ABC中,∠C=90°,AC=3,AB=5,则
SIn
4在Rt△ABC中,∠C=90°,若AC=2BC,则sinA
的值是
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第1课时 锐角三角函数(1)
课导人自主预习,检测预习效果
(一)学习目标
1.理解在直角三角形中,当锐角固定时,它的对
边与斜边的比是个固定值的事实
2.掌握正弦的概念,在直角三角形中,会求一个
锐角的正弦值.
二)课前预习
【检测1】下列命题:①sina表示角a与符号sin
的乘积②在△ABC中,若∠C=90°,则sinA
AB
BC
成立;③已知α为锐角,sina表示的是个比值.其
中真命题有
【检测2】如图1,在
R△ABC中,∠C=90°,贝
SInA=
典回澳例剥祈,名师点拨疑
★直接求锐角的正弦值
例1如图2,在△ABC中,∠ACB=90°,AC=4
BC=3,求sinA,sinB的值
分析:根据勾股定理易求出斜边AC的长,再根
据正弦的定义求sinA,sinB的值即可
变式
如图3,○O的半径为5,弦AB
的长8,则sinA的值为
例2在Rt△ABC中,∠C=909,AC=BC,求sinA
的值.
分析:由题意可知,△ABC为等腰直角三角形,所
以AC:BC:AB=1:1:V2,再根据正弦的定义即
可得出sinA的值
变式22
如图4,在△ABC中,∠ACB=90°,CD⊥AB于点
D,AD=4,CD=3,求sinB和sin∠DCB的值
B
图4
变式2snB=sin∠ACD=4
S,sin∠DCB=sinA
回味反思,领悟才能提
1.在直角三角形中,当锐角A的度数一定时,不
管三角形的大小如何,∠A的对边与斜边的比都是
2.在R△ABC中,∠C=90°,AB=C,BC=a,把
锐角A的
与的比叫做∠A的正弦,记
作
即sinA
3.正弦是在直角三角形中定义的,其本质是两条
线段的比值,是一个数值,没有单位,其大小只与锐角
的大小有关,而与锐角所在直角三角形的大小无关.
四除档训练自主练兵,会做才算懂了
A组:基础练习
1.在Rt△ABC中,∠C=90°,若将各边长度都扩
大为原来的4倍,则∠A的正弦值
().
A.扩大4倍
B.缩小4倍
C.扩大2倍
D.不变
2.在△ABC中,AC=8,BC=6,AB=10,则sinA
的值为
().
A
B.4
5
D
534
3.在Rt△ABC中,∠C=90°,AC=3,AB=5,则
SIn
4在Rt△ABC中,∠C=90°,若AC=2BC,则sinA
的值是
