89第二十八章 锐角三角函数(2)
文档属性
| 名称 | 89第二十八章 锐角三角函数(2) |

|
|
| 格式 | zip | ||
| 文件大小 | 500.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-06 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第2课时 锐角三角函数(2)
一斯課导入自主预习检测预习救果
(一)学习目标
掌握余弦、正切的定义.
2.能熟练地运用锐角三角函数的概念进行有关
的计算
(二)课前预习
B
检测1】如图1,在Rt△ABC
中,∠C=90°,则cosA
tan a
检测2】在Rt△ABC中,∠C
A
90°,BC=AC=1,则cosA=
图1
典型问题例剑析名师点坡解疑
★锐角三角函数的计算
例1在Rt△ABC中,∠C=90°,AC=6,BC=8,
求sinA,cosA和tanA
分析:在Rt△ABC中,根据勾股定理,求出斜边
AB的长,再根据三角函数的定义,求sinA,cosA和
tanA的值
变式
A
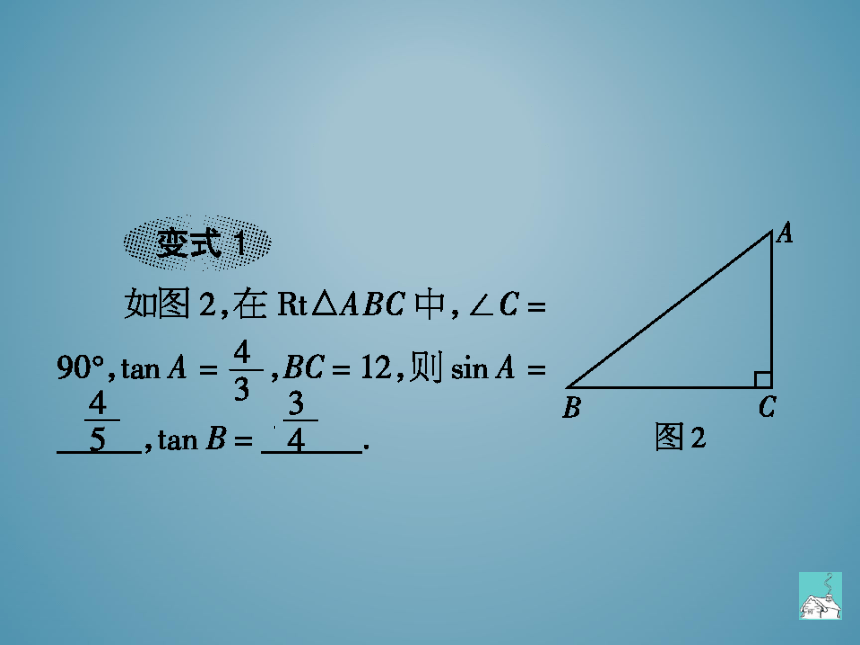
如图2,在Rt△ABC中,∠C
如mA①,BC=12,则sinA
90°,tanA
B
C
图2
★锐角三角函数的综合运用
例2如图3,正方形ABCD的边长为4,点M在
边DC上,M,N两点关于对角线AC对称,若DM
求tan∠CND的值
分析:由对称性可知,DM=BN=1,于是可求出
CN的值,在Rt△CDN中即可求得tan∠CND的值
例2∵M,N两点关于对角线AC对称,CM=CN.
CB=CD,∴BN=DM.
又∵正方形ABCD的边长为4,DM=1,CD=BC=4,
CN=CB-BNE4-DM 3
在Rt△DNC中,tam∠CMD=CD=4
CN
变式2
如图4,已知⊙O的半径为1
B
AB与⊙0相切点A,OB与⊙0交
于点C,CD⊥OA,垂足为点D,则
cos∠AOB的值等于
().
D
A OD
B OA
C CD
DAB
图4
三归纳小结回味反思领悟才能提高
.在Rt△ABC中,∠C=90°,BC=a,AB=c,
AC=b,把锐角A的与的比叫做∠A的余
弦,记作
,即cosA
;把锐角
A的
的比叫儆∠A的正切,记作
,即tanA
2.锐角A的正弦、_
都叫做∠A的
锐角三角函数
四阶構训练白主练兵,会做才算懂了
A组:基础练习
在R△ABC中,如果各边长都扩大2倍,那么
sinA,cosA,tanA的值都
A.不变
B.扩大2倍
C.扩大4倍
D缩小2倍
2.在Rt△ABC中,∠C=90°,BC=V2,AB=
√3,则卜列结论正确的是
().
A. sin a
B cos B=
C. tanA=V2
D tan B=v2
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第2课时 锐角三角函数(2)
一斯課导入自主预习检测预习救果
(一)学习目标
掌握余弦、正切的定义.
2.能熟练地运用锐角三角函数的概念进行有关
的计算
(二)课前预习
B
检测1】如图1,在Rt△ABC
中,∠C=90°,则cosA
tan a
检测2】在Rt△ABC中,∠C
A
90°,BC=AC=1,则cosA=
图1
典型问题例剑析名师点坡解疑
★锐角三角函数的计算
例1在Rt△ABC中,∠C=90°,AC=6,BC=8,
求sinA,cosA和tanA
分析:在Rt△ABC中,根据勾股定理,求出斜边
AB的长,再根据三角函数的定义,求sinA,cosA和
tanA的值
变式
A
如图2,在Rt△ABC中,∠C
如mA①,BC=12,则sinA
90°,tanA
B
C
图2
★锐角三角函数的综合运用
例2如图3,正方形ABCD的边长为4,点M在
边DC上,M,N两点关于对角线AC对称,若DM
求tan∠CND的值
分析:由对称性可知,DM=BN=1,于是可求出
CN的值,在Rt△CDN中即可求得tan∠CND的值
例2∵M,N两点关于对角线AC对称,CM=CN.
CB=CD,∴BN=DM.
又∵正方形ABCD的边长为4,DM=1,CD=BC=4,
CN=CB-BNE4-DM 3
在Rt△DNC中,tam∠CMD=CD=4
CN
变式2
如图4,已知⊙O的半径为1
B
AB与⊙0相切点A,OB与⊙0交
于点C,CD⊥OA,垂足为点D,则
cos∠AOB的值等于
().
D
A OD
B OA
C CD
DAB
图4
三归纳小结回味反思领悟才能提高
.在Rt△ABC中,∠C=90°,BC=a,AB=c,
AC=b,把锐角A的与的比叫做∠A的余
弦,记作
,即cosA
;把锐角
A的
的比叫儆∠A的正切,记作
,即tanA
2.锐角A的正弦、_
都叫做∠A的
锐角三角函数
四阶構训练白主练兵,会做才算懂了
A组:基础练习
在R△ABC中,如果各边长都扩大2倍,那么
sinA,cosA,tanA的值都
A.不变
B.扩大2倍
C.扩大4倍
D缩小2倍
2.在Rt△ABC中,∠C=90°,BC=V2,AB=
√3,则卜列结论正确的是
().
A. sin a
B cos B=
C. tanA=V2
D tan B=v2
