93第二十八章 解直角三角形(2)
文档属性
| 名称 | 93第二十八章 解直角三角形(2) |

|
|
| 格式 | zip | ||
| 文件大小 | 704.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-06 18:47:11 | ||
图片预览






文档简介
(共23张PPT)
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第6课时 解直角三角形(2)
新课导人自主预习检测预习效果
(一)学习目标
1.了解仰角、俯角的概念及联系
2.能根据有关的示意图,将实际问题中的数量关
系转化为解直角三角形的相关知识,从而解决测量距
离、物体的高度等问题
(二)课前预习
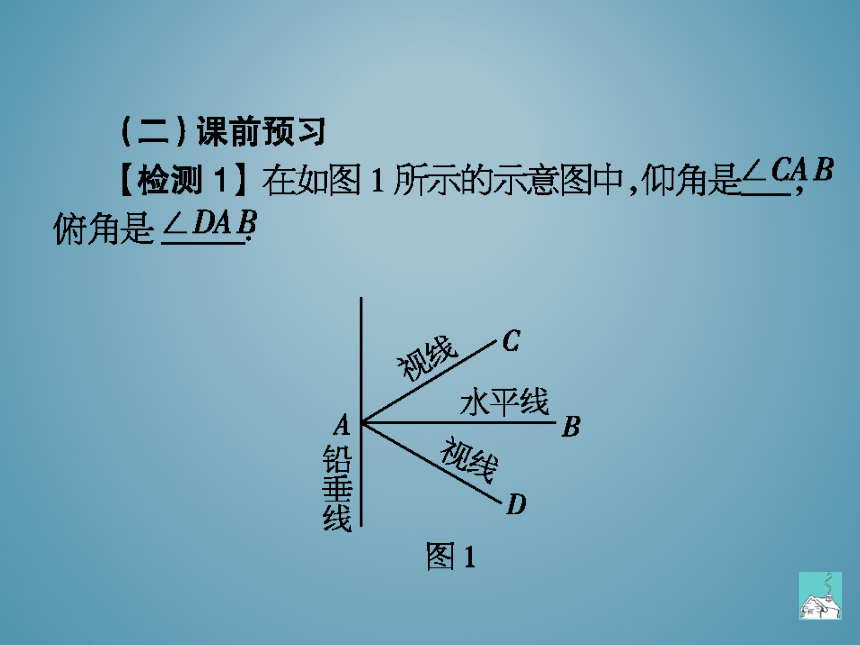
检测1】在如图1所示的示意图中,仰角是,
俯角是
C
水平线
A
B
铅垂线
D
图1
检测2】如图2,电线杆AB的中点C处有一标
志物,在地面点D处测得标志物的仰角为45°,若点
D到电线杆底部点B的距离为3m,则电线杆AB高
为
心二典型阿题典例剖析名师点拨解疑
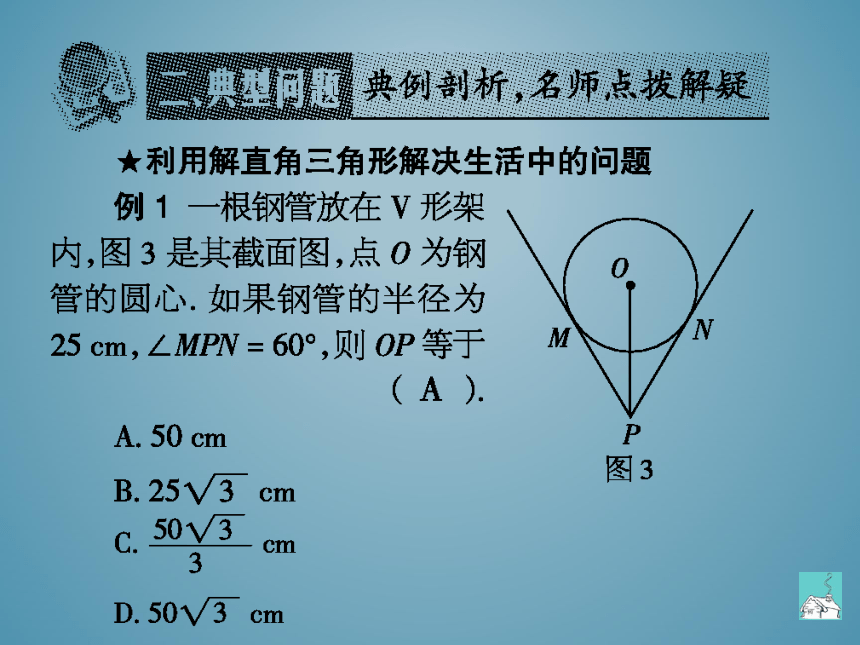
★利用解直角三角形解决生活中的问题
例1一根钢管放在ⅴ形架
内,图3是其截面图,点O为钢
管的圆心.如果钢管的半径为
25cm,∠MPN=60°,则OP等于M
N
A. 50 cm
P
图3
B. 25V3 cm
分析:连接OM,ON,易得到两个全等的直角三角
形,可在任何一个直角三角形中,利用三角函数求OP
的长
变式
如图4,放置在水平桌面上的台灯的灯臂AB长
为40cm,灯罩BC长为30cm,底座厚度为2cm,灯
臂与底座构成的∠BAD=60.使用发现,光线最佳时
灯罩BC与水平线所成的角为30°,此时灯罩顶端
C到桌面的高度CE是多少(结果精确到0.1cm,
V3≈1.732)
C
309x
B
60A
E
图4
变式1过点B作BF⊥CD于点F作BG⊥AD于点G
在Rt△BCF中,∠CBF=30°,
∴CF=BC·sin30°=30x
15.
2
在Rt△ABG中,∠BAG=60
BG=AB,sin60°=40×3=20V3
2
CE=CF+F+DE=15+20√3+2=17+20V3
5164≈516(cm)
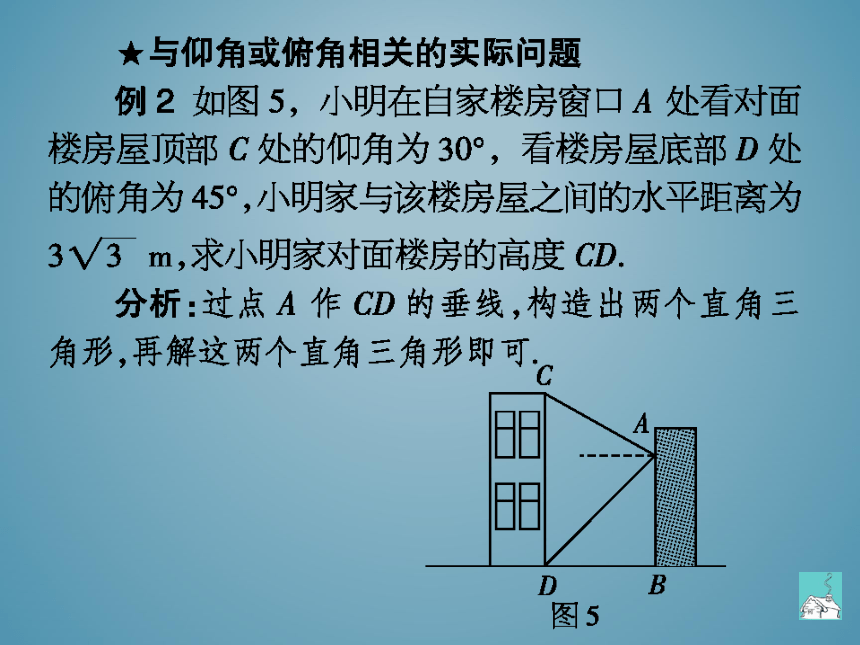
★与仰角或俯角相关的实际问题
例2如图5,小明在自家楼房窗口A处看对面
楼房屋顶部C处的仰角为30°,看楼房屋底部D处
的俯角为45°,小明家与该楼房屋之间的水平距离为
3V3m,求小明家对面楼房的高度CD
分析:过点A作CD的垂线,构造出两个直角三
角形,再解这两个直角三角形即可
D
B
图
例2作AE⊥CD于点E
由题意可知∠CAE=30°,∠EAD=45°,AE=3V3m
在Rt△ACE中,an∠CAE=CE,即tan30=CE
AE
3V3
CE=3V3tan30°=3v3
=3(m)
在Rt△AED中,∠ADE=90°-∠EAD=909-45
45°,DE=AE=3V3(m)
∴DC=CE+DE=(3+3V3)m,
楼房的高度DC为(3+3V3)m
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第6课时 解直角三角形(2)
新课导人自主预习检测预习效果
(一)学习目标
1.了解仰角、俯角的概念及联系
2.能根据有关的示意图,将实际问题中的数量关
系转化为解直角三角形的相关知识,从而解决测量距
离、物体的高度等问题
(二)课前预习
检测1】在如图1所示的示意图中,仰角是,
俯角是
C
水平线
A
B
铅垂线
D
图1
检测2】如图2,电线杆AB的中点C处有一标
志物,在地面点D处测得标志物的仰角为45°,若点
D到电线杆底部点B的距离为3m,则电线杆AB高
为
心二典型阿题典例剖析名师点拨解疑
★利用解直角三角形解决生活中的问题
例1一根钢管放在ⅴ形架
内,图3是其截面图,点O为钢
管的圆心.如果钢管的半径为
25cm,∠MPN=60°,则OP等于M
N
A. 50 cm
P
图3
B. 25V3 cm
分析:连接OM,ON,易得到两个全等的直角三角
形,可在任何一个直角三角形中,利用三角函数求OP
的长
变式
如图4,放置在水平桌面上的台灯的灯臂AB长
为40cm,灯罩BC长为30cm,底座厚度为2cm,灯
臂与底座构成的∠BAD=60.使用发现,光线最佳时
灯罩BC与水平线所成的角为30°,此时灯罩顶端
C到桌面的高度CE是多少(结果精确到0.1cm,
V3≈1.732)
C
309x
B
60A
E
图4
变式1过点B作BF⊥CD于点F作BG⊥AD于点G
在Rt△BCF中,∠CBF=30°,
∴CF=BC·sin30°=30x
15.
2
在Rt△ABG中,∠BAG=60
BG=AB,sin60°=40×3=20V3
2
CE=CF+F+DE=15+20√3+2=17+20V3
5164≈516(cm)
★与仰角或俯角相关的实际问题
例2如图5,小明在自家楼房窗口A处看对面
楼房屋顶部C处的仰角为30°,看楼房屋底部D处
的俯角为45°,小明家与该楼房屋之间的水平距离为
3V3m,求小明家对面楼房的高度CD
分析:过点A作CD的垂线,构造出两个直角三
角形,再解这两个直角三角形即可
D
B
图
例2作AE⊥CD于点E
由题意可知∠CAE=30°,∠EAD=45°,AE=3V3m
在Rt△ACE中,an∠CAE=CE,即tan30=CE
AE
3V3
CE=3V3tan30°=3v3
=3(m)
在Rt△AED中,∠ADE=90°-∠EAD=909-45
45°,DE=AE=3V3(m)
∴DC=CE+DE=(3+3V3)m,
楼房的高度DC为(3+3V3)m
