高中数学人教A版(2019)选择性必修第一册第二章2.3.1两条直线的交点坐标 课件(共32张PPT)
文档属性
| 名称 | 高中数学人教A版(2019)选择性必修第一册第二章2.3.1两条直线的交点坐标 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 779.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 00:00:00 | ||
图片预览











文档简介
两条直线的交点坐标
温故知新
点
直线l:
在直线l上
问题1:已知两条直线 ,
相交,如何求得两条直线的交点坐标?
联立方程组
?
解得
?
即为两条直线交点坐标.
直线 和 存在唯一交点,记为
直线 和 相交.
点 既在 上,又在 上.
????????????????是方程组 的唯一解.
?
直线 和 存在唯一交点,记为
直线 和 相交.
点 既在 上,又在 上.
????????????????是方程组 的唯一解.
?
直线 和 存在唯一交点,记为
直线 和 相交.
点 既在 上,又在 上.
????????????????是方程组 的唯一解.
?
问题1:已知两条直线 ,
相交,如何求得两条直线的交点坐标?
联立方程组
?
解得
?
即为两条直线交点坐标.
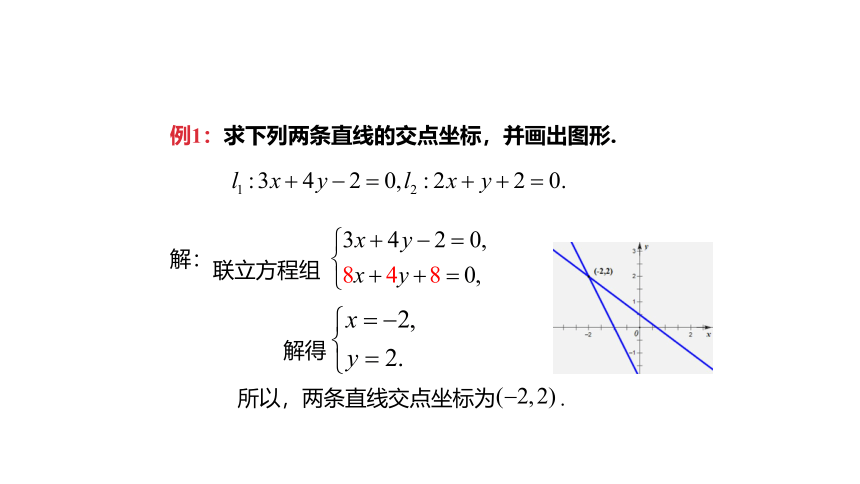
例1:求下列两条直线的交点坐标,并画出图形.
解:
联立方程组
?
例1:求下列两条直线的交点坐标,并画出图形.
解:
联立方程组
?
所以,两条直线交点坐标为 .
解得
?
直线 和 存在唯一交点,记为
直线 和 相交.
直线相交
方程组有
唯一解
点 既在 上,又在 上.
????????????????是方程组 的唯一解.
?
问题2:如果两条直线 ,
平行,能否判断对应方程组解的情况?
没有公共点
不存在点同时满足两条直线方程
方程组无解
问题2:如果两条直线 ,
平行,能否判断对应方程组解的情况?
没有公共点
不存在点同时满足两条直线方程
方程组无解
问题2:如果两条直线 ,
平行,能否判断对应方程组解的情况?
没有公共点
不存在点同时满足两条直线方程
方程组无解
问题2:如果两条直线 ,
平行,能否判断对应方程组解的情况?
没有公共点
不存在点同时满足两条直线方程
方程组无解
问题2:如果两条直线 ,
平行,能否判断对应方程组解的情况?
没有公共点
不存在点同时满足两条直线方程
方程组无解
问题3:如果两条直线 ,
重合,能否判断对应方程组解的情况?
有无数个公共点
存在无数个点同时满足两条直线方程
方程组有无数组解
直线 和 重合
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}直线的位置关系
公共点的个数
方程组解的个数
相交
平行
重合
有且仅有1个
唯一解
0个
无解
无数个
无数组解
两条直线的位置关系与对应的二元一次方程组解的个数
例2:判断下列各对直线的位置关系.如果相交,求出交点的坐标.
解:
联立方程组
?
所以,两条直线交点坐标为 .
解得
?
例2:判断下列各对直线的位置关系.如果相交,求出交点的坐标.
所以,两条直线平行.
解:
联立方程组
?
解得 , 矛盾.
方程组无解,
对于斜率分别为 的两条直线 ,有
追问1:如果题目改为只问“判断下列各对直线的位置关系”,你还有没有其他的判断方法?
追问2:能否用斜率判断两对直线的位置关系?
追问3:如何从直线方程的一般式中确定斜率?
解:(1) 将两条直线方程化为斜截式:
斜率不等, 与 相交.
≠
?
追问2:能否用斜率判断两对直线的位置关系?
解:
斜率相等,截距不等,则 与 平行.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}斜率判断
解方程组判断
追问3:能否用直线斜率和解方程组,这两种方法判断两条直线 的位置关系,并确定交点个数呢?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}斜率判断
解方程组判断
与 重合,有无数个交点.
追问3:能否用直线斜率和解方程组,这两种方法判断两条直线 的位置关系,并确定交点个数呢?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}斜率判断
解方程组判断
与 重合,有无数个交点.
两个方程相同,方程组有无数个解.
追问3:能否用直线斜率和解方程组,这两种方法判断两条直线 的位置关系,并确定交点个数呢?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}斜率判断
解方程组判断
与 重合,有无数个交点,交点坐标满足方程 .
追问3:能否用直线斜率和解方程组,这两种方法判断两条直线 的位置关系,并确定交点个数呢?
问题4:比较用斜率判断和解方程组判断两直线位置关系,你有什么体会?
斜率判断解方程组判断
?
代数方法
关注直线方程系数关系,快速判断两条直线平行或相交(垂直).
关注解的个数与交点个数的对应,判断两条直线平行或相交;
求相交直线交点坐标.
例3:求满足下列条件的直线 的方程:
(1) 经过两条直线 和 的交点,且平行于直线 .
追问1:求解直线方程需要具备哪些条件?
追问2:分析本题中的条件,能获得哪些确定直线
的信息?
例3:求满足下列条件的直线 的方程:
(1) 经过两条直线 和 的交点,且平行于直线 .
解:联立方程组
?
由直线 l 与 平行知,l的斜率为 .
整理得
解得交点坐标为 .
所以直线 l 的方程为 ,
例3:求满足下列条件的直线 的方程:
(2) 经过两条直线 和 的交点,且垂直于直线 .
追问4:两条直线垂直,斜率有何关系?
求交点
求斜率
点斜式
例3:求满足下列条件的直线 的方程:
(2) 经过两条直线 和 的交点,且垂直于直线 .
解:联立方程组
?
例3:求满足下列条件的直线 的方程:
(2) 经过两条直线 和 的交点,且垂直于直线 .
解:联立方程组
?
由直线 l 与 垂直知,l的斜率为 .
解得交点坐标为 .
整理得
所以直线 l 的方程为 ,
回顾本节课的探究过程,说一说你学到了什么?
求相交直线交点坐标
解方程组
判断两条直线的位置关系
(相交、平行、重合)
解的个数与交点个数的对应
课堂小结
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}直线的位置关系
公共点的个数
方程组解的个数
相交
平行
重合
有且仅有1个
唯一解
0个
无解
无数个
无数组解
两条直线的位置关系与对应的二元一次方程组解的个数
课后作业
1.求下列两条直线的交点坐标,并画出图象.
(1)
(2)
2.判断下列各对直线的位置关系,如果相交,求出交点的坐标:
(1)
(2)
(3)
温故知新
点
直线l:
在直线l上
问题1:已知两条直线 ,
相交,如何求得两条直线的交点坐标?
联立方程组
?
解得
?
即为两条直线交点坐标.
直线 和 存在唯一交点,记为
直线 和 相交.
点 既在 上,又在 上.
????????????????是方程组 的唯一解.
?
直线 和 存在唯一交点,记为
直线 和 相交.
点 既在 上,又在 上.
????????????????是方程组 的唯一解.
?
直线 和 存在唯一交点,记为
直线 和 相交.
点 既在 上,又在 上.
????????????????是方程组 的唯一解.
?
问题1:已知两条直线 ,
相交,如何求得两条直线的交点坐标?
联立方程组
?
解得
?
即为两条直线交点坐标.
例1:求下列两条直线的交点坐标,并画出图形.
解:
联立方程组
?
例1:求下列两条直线的交点坐标,并画出图形.
解:
联立方程组
?
所以,两条直线交点坐标为 .
解得
?
直线 和 存在唯一交点,记为
直线 和 相交.
直线相交
方程组有
唯一解
点 既在 上,又在 上.
????????????????是方程组 的唯一解.
?
问题2:如果两条直线 ,
平行,能否判断对应方程组解的情况?
没有公共点
不存在点同时满足两条直线方程
方程组无解
问题2:如果两条直线 ,
平行,能否判断对应方程组解的情况?
没有公共点
不存在点同时满足两条直线方程
方程组无解
问题2:如果两条直线 ,
平行,能否判断对应方程组解的情况?
没有公共点
不存在点同时满足两条直线方程
方程组无解
问题2:如果两条直线 ,
平行,能否判断对应方程组解的情况?
没有公共点
不存在点同时满足两条直线方程
方程组无解
问题2:如果两条直线 ,
平行,能否判断对应方程组解的情况?
没有公共点
不存在点同时满足两条直线方程
方程组无解
问题3:如果两条直线 ,
重合,能否判断对应方程组解的情况?
有无数个公共点
存在无数个点同时满足两条直线方程
方程组有无数组解
直线 和 重合
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}直线的位置关系
公共点的个数
方程组解的个数
相交
平行
重合
有且仅有1个
唯一解
0个
无解
无数个
无数组解
两条直线的位置关系与对应的二元一次方程组解的个数
例2:判断下列各对直线的位置关系.如果相交,求出交点的坐标.
解:
联立方程组
?
所以,两条直线交点坐标为 .
解得
?
例2:判断下列各对直线的位置关系.如果相交,求出交点的坐标.
所以,两条直线平行.
解:
联立方程组
?
解得 , 矛盾.
方程组无解,
对于斜率分别为 的两条直线 ,有
追问1:如果题目改为只问“判断下列各对直线的位置关系”,你还有没有其他的判断方法?
追问2:能否用斜率判断两对直线的位置关系?
追问3:如何从直线方程的一般式中确定斜率?
解:(1) 将两条直线方程化为斜截式:
斜率不等, 与 相交.
≠
?
追问2:能否用斜率判断两对直线的位置关系?
解:
斜率相等,截距不等,则 与 平行.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}斜率判断
解方程组判断
追问3:能否用直线斜率和解方程组,这两种方法判断两条直线 的位置关系,并确定交点个数呢?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}斜率判断
解方程组判断
与 重合,有无数个交点.
追问3:能否用直线斜率和解方程组,这两种方法判断两条直线 的位置关系,并确定交点个数呢?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}斜率判断
解方程组判断
与 重合,有无数个交点.
两个方程相同,方程组有无数个解.
追问3:能否用直线斜率和解方程组,这两种方法判断两条直线 的位置关系,并确定交点个数呢?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}斜率判断
解方程组判断
与 重合,有无数个交点,交点坐标满足方程 .
追问3:能否用直线斜率和解方程组,这两种方法判断两条直线 的位置关系,并确定交点个数呢?
问题4:比较用斜率判断和解方程组判断两直线位置关系,你有什么体会?
斜率判断解方程组判断
?
代数方法
关注直线方程系数关系,快速判断两条直线平行或相交(垂直).
关注解的个数与交点个数的对应,判断两条直线平行或相交;
求相交直线交点坐标.
例3:求满足下列条件的直线 的方程:
(1) 经过两条直线 和 的交点,且平行于直线 .
追问1:求解直线方程需要具备哪些条件?
追问2:分析本题中的条件,能获得哪些确定直线
的信息?
例3:求满足下列条件的直线 的方程:
(1) 经过两条直线 和 的交点,且平行于直线 .
解:联立方程组
?
由直线 l 与 平行知,l的斜率为 .
整理得
解得交点坐标为 .
所以直线 l 的方程为 ,
例3:求满足下列条件的直线 的方程:
(2) 经过两条直线 和 的交点,且垂直于直线 .
追问4:两条直线垂直,斜率有何关系?
求交点
求斜率
点斜式
例3:求满足下列条件的直线 的方程:
(2) 经过两条直线 和 的交点,且垂直于直线 .
解:联立方程组
?
例3:求满足下列条件的直线 的方程:
(2) 经过两条直线 和 的交点,且垂直于直线 .
解:联立方程组
?
由直线 l 与 垂直知,l的斜率为 .
解得交点坐标为 .
整理得
所以直线 l 的方程为 ,
回顾本节课的探究过程,说一说你学到了什么?
求相交直线交点坐标
解方程组
判断两条直线的位置关系
(相交、平行、重合)
解的个数与交点个数的对应
课堂小结
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}直线的位置关系
公共点的个数
方程组解的个数
相交
平行
重合
有且仅有1个
唯一解
0个
无解
无数个
无数组解
两条直线的位置关系与对应的二元一次方程组解的个数
课后作业
1.求下列两条直线的交点坐标,并画出图象.
(1)
(2)
2.判断下列各对直线的位置关系,如果相交,求出交点的坐标:
(1)
(2)
(3)
