高中数学人教A版(2019)选择性必修第一册第二章2.3.2两点间的距离公式 课件(共22张PPT)
文档属性
| 名称 | 高中数学人教A版(2019)选择性必修第一册第二章2.3.2两点间的距离公式 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 678.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 19:53:33 | ||
图片预览







文档简介
两点间的距离公式
问题1:如图,已知平面内两点 如何求 间的距离 ?
追问1:我们学过什么知识可以刻画平面直角坐标系内两点间线段的长度?
追问1:我们学过什么知识可以刻画平面直角坐标系内两点间线段的长度?
追问2:如何求向量 的模长?
特别地,原点 与任一点 间的距离是
已知平面内两点 ,则两点间的距离公式是
A
追问4:能否利用 构造直角三角形,求线段的长度?基于点坐标的意义,你能构造出适当的直角三角形吗?
A
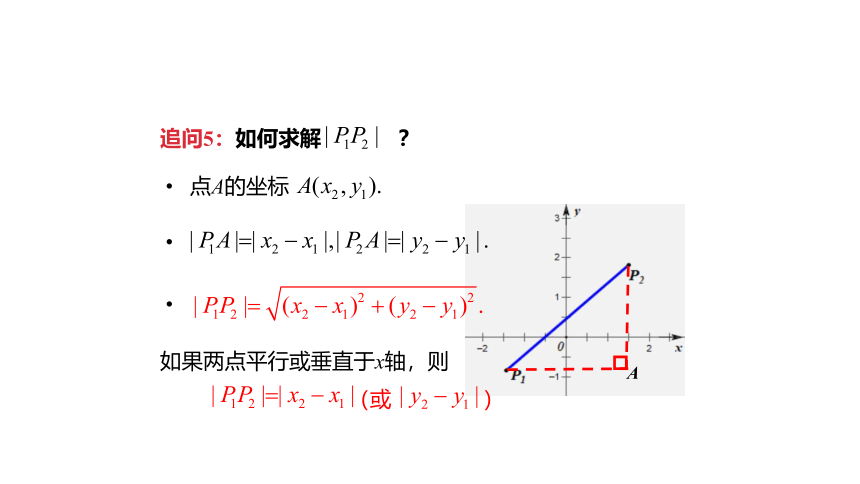
追问5:如何求解 ?
点A的坐标
如果两点平行或垂直于x轴,则
(或 )
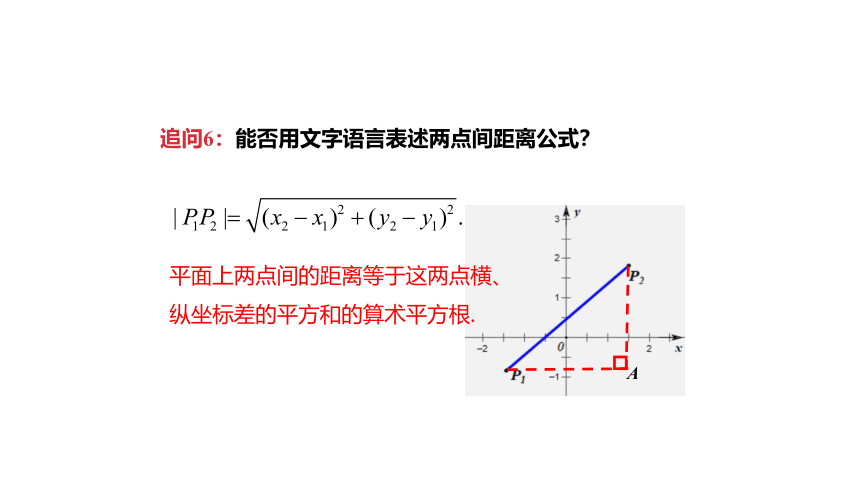
追问6:能否用文字语言表述两点间距离公式?
A
平面上两点间的距离等于这两点横、纵坐标差的平方和的算术平方根.
解:设所求点
例1:已知点 ,在 轴上求一点 ,
使得 ,并求出 的值.
则
由 ,得
解得,
解:设所求点
例1:已知点 ,在 轴上求一点 ,
使得 ,并求出 的值.
所以,
例1:已知点 ,在 轴上求一点 ,
使得 ,并求出 的值.
点C的坐标
AB垂直平分线的斜率是
AB垂直平分线的方程是
例1:已知点 ,在 轴上求一点 ,
使得 ,并求出 的值.
AB垂直平分线的方程是
令 ,
所以,
解得,
例1:已知点 ,在 轴上求一点 ,
使得 ,并求出 的值.
法1:设点 P 坐标,
由线段相等,建立关于点 P 的方程,
解方程,求点 P 及| PA |.
求线段 AB 的垂直平分线方程,
联立垂直平分线方程与x轴方程,求交点 P 的坐标,
解方程,求点 P 及| PA |.
法2:由| PA |= | PB|判断出点 P 在线段 AB 的垂直平分线上,
列
解
设
形
数
数
例2:用坐标法证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
追问2:如何建立适当的平面直角坐标系?用坐标表示哪些量呢?
追问1:什么是坐标法?
例2:用坐标法证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
x
y
追问3:结合平行四边形的性质,说说需要设出哪些点的坐标?
追问4:如何用顶点坐标表示对角线的长度及边长?
例2:用坐标法证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
所以,
x
y
例2:用坐标法证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
所以,
x
y
——广义勾股定理
例2:用坐标法证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
建立坐标系,用图形点的坐标表示有关的量
进行相关代数运算——坐标表示线段长度
把代数运算结果“翻译”成几何结论
例2:用坐标法证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
建立坐标系,用图形点的坐标表示有关的量
进行相关代数运算——坐标表示线段长度
把代数运算结果“翻译”成几何结论
例2:用坐标法证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
追问5:还可以怎么建系呢?
x
y
O
追问6:如何设点的坐标?
追问7:如何用坐标表示所求线段的长度?
例2:用坐标法证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
x
y
O
所以,
例2:用坐标法证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
x
y
O
x
y
追问8:两种建系方法都算是“适当”的方法,其原因在何?
例2:用坐标法证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
x
y
O
x
y
O
A
B
C
D
追问9:我们曾经用向量法证明过这个结论,你能回忆一下证明过程吗?
用 表示两条对角线向量,计算所求量间的关系.
取 为基底,
代数结果“翻译”成几何结论
已知两点 能否说出这两点间的距离公式?
课堂小结
能否描述这句话对应的几何图形?
课堂小结
A
两点间距离公式的证明
回顾两道例题的求解过程,总结它们的共同点,谈谈你的感受?
代数
几何
几何
坐标
课后作业
1.用“向量法”及另一种建立坐标系的方法证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
2.已知 与 两点间的距离是17,求 a 的值.
3.(1)求在 x 轴上与点 的距离为13的点的坐标;
(2)已知点 P 的横坐标为7,点 P 与点 间的距离等于10,求 点 P 的坐标.
问题1:如图,已知平面内两点 如何求 间的距离 ?
追问1:我们学过什么知识可以刻画平面直角坐标系内两点间线段的长度?
追问1:我们学过什么知识可以刻画平面直角坐标系内两点间线段的长度?
追问2:如何求向量 的模长?
特别地,原点 与任一点 间的距离是
已知平面内两点 ,则两点间的距离公式是
A
追问4:能否利用 构造直角三角形,求线段的长度?基于点坐标的意义,你能构造出适当的直角三角形吗?
A
追问5:如何求解 ?
点A的坐标
如果两点平行或垂直于x轴,则
(或 )
追问6:能否用文字语言表述两点间距离公式?
A
平面上两点间的距离等于这两点横、纵坐标差的平方和的算术平方根.
解:设所求点
例1:已知点 ,在 轴上求一点 ,
使得 ,并求出 的值.
则
由 ,得
解得,
解:设所求点
例1:已知点 ,在 轴上求一点 ,
使得 ,并求出 的值.
所以,
例1:已知点 ,在 轴上求一点 ,
使得 ,并求出 的值.
点C的坐标
AB垂直平分线的斜率是
AB垂直平分线的方程是
例1:已知点 ,在 轴上求一点 ,
使得 ,并求出 的值.
AB垂直平分线的方程是
令 ,
所以,
解得,
例1:已知点 ,在 轴上求一点 ,
使得 ,并求出 的值.
法1:设点 P 坐标,
由线段相等,建立关于点 P 的方程,
解方程,求点 P 及| PA |.
求线段 AB 的垂直平分线方程,
联立垂直平分线方程与x轴方程,求交点 P 的坐标,
解方程,求点 P 及| PA |.
法2:由| PA |= | PB|判断出点 P 在线段 AB 的垂直平分线上,
列
解
设
形
数
数
例2:用坐标法证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
追问2:如何建立适当的平面直角坐标系?用坐标表示哪些量呢?
追问1:什么是坐标法?
例2:用坐标法证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
x
y
追问3:结合平行四边形的性质,说说需要设出哪些点的坐标?
追问4:如何用顶点坐标表示对角线的长度及边长?
例2:用坐标法证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
所以,
x
y
例2:用坐标法证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
所以,
x
y
——广义勾股定理
例2:用坐标法证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
建立坐标系,用图形点的坐标表示有关的量
进行相关代数运算——坐标表示线段长度
把代数运算结果“翻译”成几何结论
例2:用坐标法证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
建立坐标系,用图形点的坐标表示有关的量
进行相关代数运算——坐标表示线段长度
把代数运算结果“翻译”成几何结论
例2:用坐标法证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
追问5:还可以怎么建系呢?
x
y
O
追问6:如何设点的坐标?
追问7:如何用坐标表示所求线段的长度?
例2:用坐标法证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
x
y
O
所以,
例2:用坐标法证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
x
y
O
x
y
追问8:两种建系方法都算是“适当”的方法,其原因在何?
例2:用坐标法证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
x
y
O
x
y
O
A
B
C
D
追问9:我们曾经用向量法证明过这个结论,你能回忆一下证明过程吗?
用 表示两条对角线向量,计算所求量间的关系.
取 为基底,
代数结果“翻译”成几何结论
已知两点 能否说出这两点间的距离公式?
课堂小结
能否描述这句话对应的几何图形?
课堂小结
A
两点间距离公式的证明
回顾两道例题的求解过程,总结它们的共同点,谈谈你的感受?
代数
几何
几何
坐标
课后作业
1.用“向量法”及另一种建立坐标系的方法证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
2.已知 与 两点间的距离是17,求 a 的值.
3.(1)求在 x 轴上与点 的距离为13的点的坐标;
(2)已知点 P 的横坐标为7,点 P 与点 间的距离等于10,求 点 P 的坐标.
