94第二十八章 解直角三角形(3)
文档属性
| 名称 | 94第二十八章 解直角三角形(3) |  | |
| 格式 | zip | ||
| 文件大小 | 621.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-06 18:47:11 | ||
图片预览






文档简介
(共23张PPT)
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第7课时 解直角三角形(3)
导A自主预习,检测预习效果
(一)学习目标
理解方位角、坡角、坡度等概念.
2.能根据题意,将涉及航行、坡度等实际问题转
化为解直角三角形的相关问题加以解决
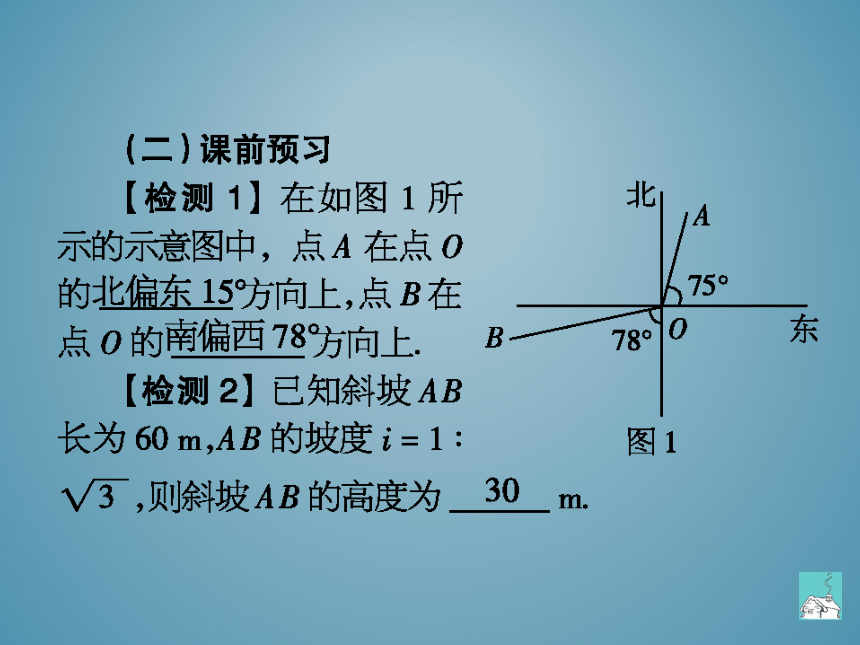
(二)课前预习
检测1】在如图1所
北
示的示意图中,点A在点O
的
方向上,点B在
75°
点O的
方向上.B
78
东
检测2】已知斜坡AB
长为60m,AB的坡度讠=1
图1
V3,则斜坡AB的高度为
匚典整题典创制析,名师点教解疑
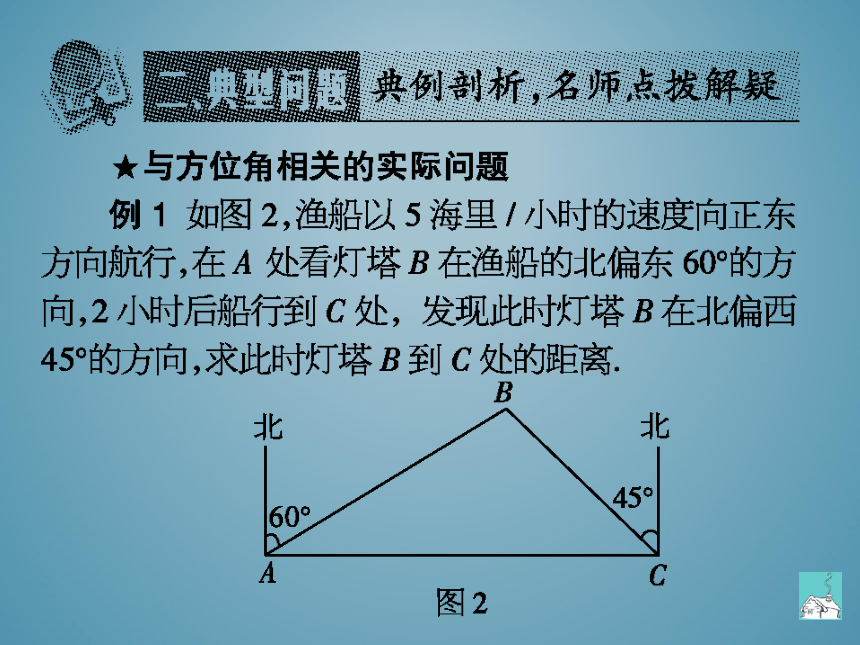
★与方位角相关的实际问题
例1如图2,渔船以5海里/小时的速度向正东
方向航行,在A处看灯塔B在渔船的北偏东609的方
向,2小时后船行到C处,发现此时灯塔B在北偏西
45的方向,求此时灯塔B到C处的距离
B
北
北
45°
609
C
图2
分析:过点B作BD⊥AC于点D,得到两个直角
三角形:Rt△ABD和Rt△CBD,分别解这两个直角三
角形,即可求出BC的长
变式1
如图3,在一次数学课外活动中,小明同学在点P
处测得教学楼A位于北偏东60°方向,办公楼B位于
南偏东459方向.小明沿正东方向前进60m到达C
处,此时测得教学楼A恰好位于正北方向,办公楼B
正好位于正南方向.求教学楼A与办公楼B之间的
距离
60
C
45
B
图3
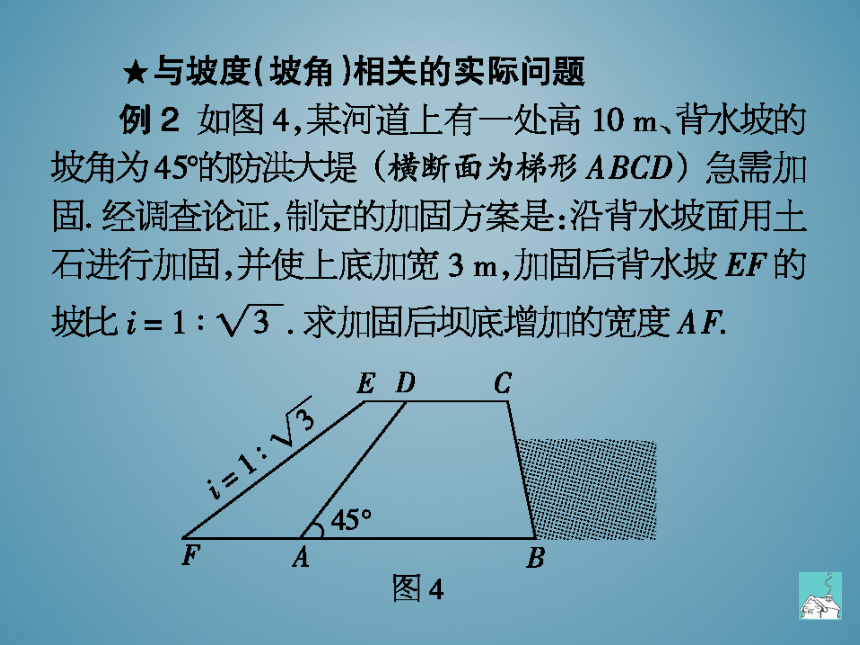
★与坡度(坡角)相关的实际问题
例2如图4,某河道上有一处高10m、背水坡的
坡角为45的洪大堤(横断面为梯形ABCD)急需加
固.经调查论证,制定的加固方案是:沿背水坡面用土
石进行加固,并使上底加宽3m,加固后背水坡EF的
坡比i=1:√3.求加固后坝底增加的宽度AF.
E D
45°
A
B
图4
分析:分别过点E,D作EG⊥AB、DH⊥AB于点G,
H,连接DF,在Rt△ADH和Rt△FDH中,分别解直角
三角形求得AF的长
例2过D作DH⊥AB于点H,过E作EG⊥AB于
点G,则AF=FG+GH-AH=10V3+3-10
(10√3-7)m
变式2
某学校教学楼后面靠近一座山坡,坡面上是一块
平地,如图5所示,BC∥AD,斜坡AB=40m,坡角
∠BAD=60°,为防夏季因瀑雨引发山体滑坡,保障安
全,学校决定对山坡进行改造,经地质人员勘测,当坡
角不超过45°时,可确保山体不滑坡,改造时保持坡
脚A不动,从坡顶B沿BC削进到E处,问BE至少
是多少
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第7课时 解直角三角形(3)
导A自主预习,检测预习效果
(一)学习目标
理解方位角、坡角、坡度等概念.
2.能根据题意,将涉及航行、坡度等实际问题转
化为解直角三角形的相关问题加以解决
(二)课前预习
检测1】在如图1所
北
示的示意图中,点A在点O
的
方向上,点B在
75°
点O的
方向上.B
78
东
检测2】已知斜坡AB
长为60m,AB的坡度讠=1
图1
V3,则斜坡AB的高度为
匚典整题典创制析,名师点教解疑
★与方位角相关的实际问题
例1如图2,渔船以5海里/小时的速度向正东
方向航行,在A处看灯塔B在渔船的北偏东609的方
向,2小时后船行到C处,发现此时灯塔B在北偏西
45的方向,求此时灯塔B到C处的距离
B
北
北
45°
609
C
图2
分析:过点B作BD⊥AC于点D,得到两个直角
三角形:Rt△ABD和Rt△CBD,分别解这两个直角三
角形,即可求出BC的长
变式1
如图3,在一次数学课外活动中,小明同学在点P
处测得教学楼A位于北偏东60°方向,办公楼B位于
南偏东459方向.小明沿正东方向前进60m到达C
处,此时测得教学楼A恰好位于正北方向,办公楼B
正好位于正南方向.求教学楼A与办公楼B之间的
距离
60
C
45
B
图3
★与坡度(坡角)相关的实际问题
例2如图4,某河道上有一处高10m、背水坡的
坡角为45的洪大堤(横断面为梯形ABCD)急需加
固.经调查论证,制定的加固方案是:沿背水坡面用土
石进行加固,并使上底加宽3m,加固后背水坡EF的
坡比i=1:√3.求加固后坝底增加的宽度AF.
E D
45°
A
B
图4
分析:分别过点E,D作EG⊥AB、DH⊥AB于点G,
H,连接DF,在Rt△ADH和Rt△FDH中,分别解直角
三角形求得AF的长
例2过D作DH⊥AB于点H,过E作EG⊥AB于
点G,则AF=FG+GH-AH=10V3+3-10
(10√3-7)m
变式2
某学校教学楼后面靠近一座山坡,坡面上是一块
平地,如图5所示,BC∥AD,斜坡AB=40m,坡角
∠BAD=60°,为防夏季因瀑雨引发山体滑坡,保障安
全,学校决定对山坡进行改造,经地质人员勘测,当坡
角不超过45°时,可确保山体不滑坡,改造时保持坡
脚A不动,从坡顶B沿BC削进到E处,问BE至少
是多少
