100第二十九章 视图(2)
文档属性
| 名称 | 100第二十九章 视图(2) |

|
|
| 格式 | zip | ||
| 文件大小 | 587.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-06 18:47:11 | ||
图片预览





文档简介
(共24张PPT)
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第2课时 视图(1)
亠断导人自主预习,检测预习效采
(一)学习目标
会根据三视图想象出立体图形或实物
2.能根据三视图的尺寸求立体图形的表面积或
体积
二)课前预习
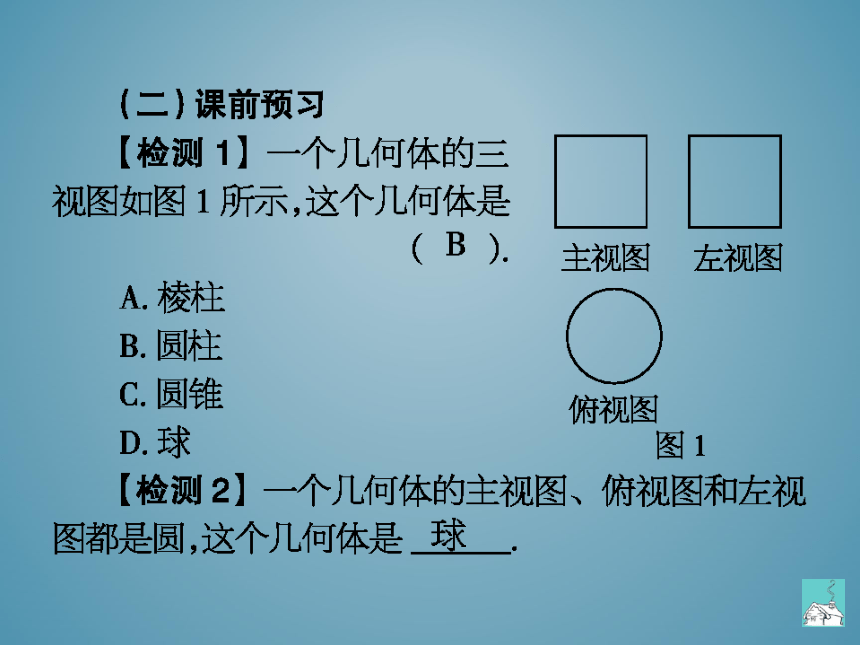
检测1】一个几何体的三
视图如图1所示,这个几何体是
().主视图左视图
A.棱
B.圆柱
C.圆锥
俯视图
D球
图1
检测2】一个几何体的主视图、俯视图和左视
图都是圆,这个几何体是
典型间题典例剖析,名师点拨解疑
★由三视图想象实物模型
例1一个实物的三视图如图2所示,描述这个
实物的形状并画出草图.
分析:由俯视图可知,物体上面是一个正六边形
和一个圆形,再综合主视图和左视图可知,它是正中
被挖去一个圆柱的六棱柱
主视图
左视图
俯视图
图2
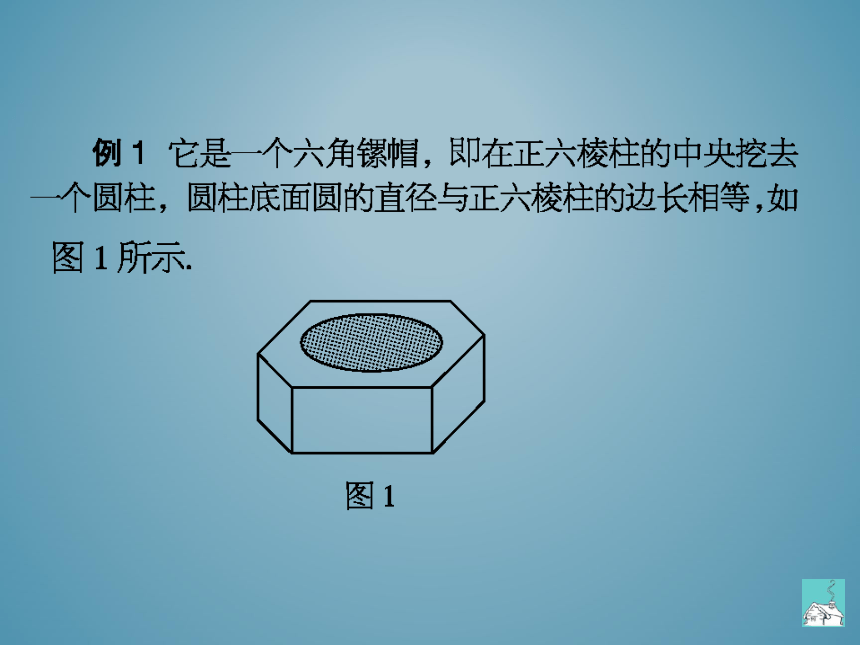
例1它是个六角镙帽,即在正六棱柱的中央挖去
个圆柱,圆柱底面圆的直径与正六棱柱的边长相等,如
图1所示
图1
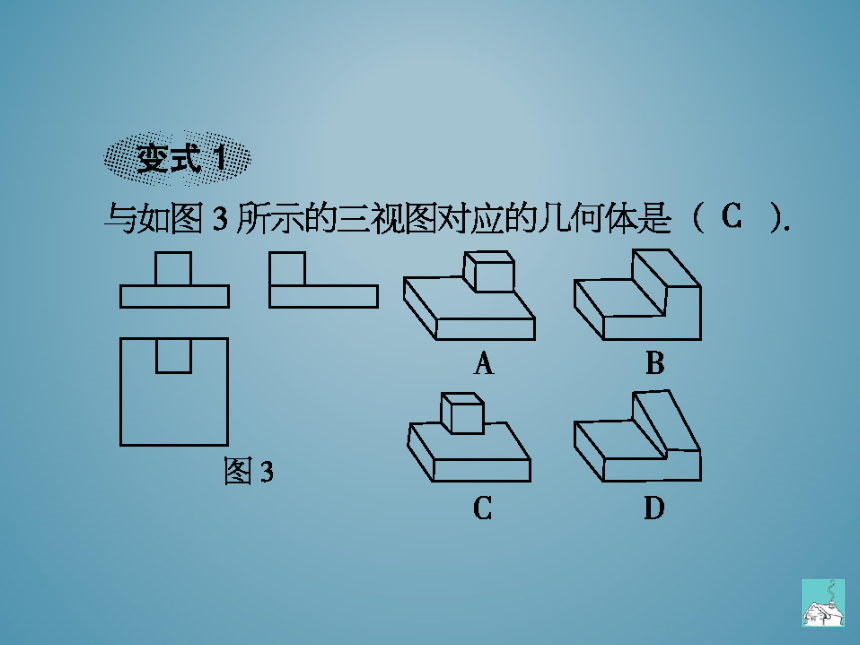
变式1
与如图3所示的三视图对应的几何体是(
A
B
图3
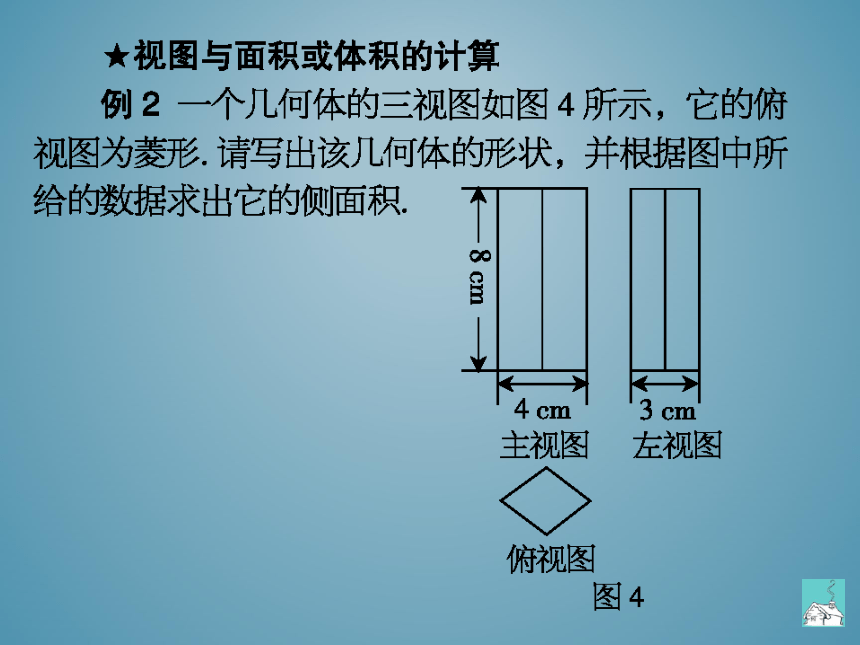
★视图与面积或体积的计算
例2一个几何体的三视图如图4所示,它的俯
视图为娄形.请写出该几何体的形状,并根据图中所
给的数据求出它的侧面积
g
4 cm3 cm
主视图左视图
俯视图
图4
分析:由三视图可知,它表示的几何体是一个底
面为菱形的四棱柱,它的侧面由四个相同的矩形组成
例2该几何体的形状是底面为菱形的直四棱柱(答直
棱柱,四棱柱,棱柱也对).由三视图知,该棱柱底面菱形的
对角线长分别为4cm,3cm
菱形的边长为cm,
棱柱的侧面积
8×4=80(cm2)
变式2
某物体的二视图如图5所示(单位:mm),它的体
积
Imm
主视图
俯视图
图5
夕三妇办结回味反思,领悟才能提
由三视图想象立体图形时,要先分别根据主视
图俯视图和左视图想象立体图形的前面、上面和左
侧面,然后再综合起来考虑整体图形
2.根据三视图求面积或体积时,可先想象出立体
图形,再进行计算
[四阶梯训练自主练兵会做才算谨了
A组:基础练习
一个几何体的三视图如图6所示,那么这个几
何体是
()
主视图左视图
A
B
俯视图
图
C
2.与图7中的三视图相对应的几何体是()
B
图7
C
D
3.若一个物体的主视图与左视图都是矩形,则这
个物体可能是
(填写一个即可)
4.一个几何体的三视图如图8所示(其中标注的
a,b,c为相应的边长),则这个几何体的体积是
图8
一、新课导入
二、典型问题
三、归纳小结
四、阶梯训练
五、考题链接
第2课时 视图(1)
亠断导人自主预习,检测预习效采
(一)学习目标
会根据三视图想象出立体图形或实物
2.能根据三视图的尺寸求立体图形的表面积或
体积
二)课前预习
检测1】一个几何体的三
视图如图1所示,这个几何体是
().主视图左视图
A.棱
B.圆柱
C.圆锥
俯视图
D球
图1
检测2】一个几何体的主视图、俯视图和左视
图都是圆,这个几何体是
典型间题典例剖析,名师点拨解疑
★由三视图想象实物模型
例1一个实物的三视图如图2所示,描述这个
实物的形状并画出草图.
分析:由俯视图可知,物体上面是一个正六边形
和一个圆形,再综合主视图和左视图可知,它是正中
被挖去一个圆柱的六棱柱
主视图
左视图
俯视图
图2
例1它是个六角镙帽,即在正六棱柱的中央挖去
个圆柱,圆柱底面圆的直径与正六棱柱的边长相等,如
图1所示
图1
变式1
与如图3所示的三视图对应的几何体是(
A
B
图3
★视图与面积或体积的计算
例2一个几何体的三视图如图4所示,它的俯
视图为娄形.请写出该几何体的形状,并根据图中所
给的数据求出它的侧面积
g
4 cm3 cm
主视图左视图
俯视图
图4
分析:由三视图可知,它表示的几何体是一个底
面为菱形的四棱柱,它的侧面由四个相同的矩形组成
例2该几何体的形状是底面为菱形的直四棱柱(答直
棱柱,四棱柱,棱柱也对).由三视图知,该棱柱底面菱形的
对角线长分别为4cm,3cm
菱形的边长为cm,
棱柱的侧面积
8×4=80(cm2)
变式2
某物体的二视图如图5所示(单位:mm),它的体
积
Imm
主视图
俯视图
图5
夕三妇办结回味反思,领悟才能提
由三视图想象立体图形时,要先分别根据主视
图俯视图和左视图想象立体图形的前面、上面和左
侧面,然后再综合起来考虑整体图形
2.根据三视图求面积或体积时,可先想象出立体
图形,再进行计算
[四阶梯训练自主练兵会做才算谨了
A组:基础练习
一个几何体的三视图如图6所示,那么这个几
何体是
()
主视图左视图
A
B
俯视图
图
C
2.与图7中的三视图相对应的几何体是()
B
图7
C
D
3.若一个物体的主视图与左视图都是矩形,则这
个物体可能是
(填写一个即可)
4.一个几何体的三视图如图8所示(其中标注的
a,b,c为相应的边长),则这个几何体的体积是
图8
