人教版B版,选修1-1,抛物线的几何性质
文档属性
| 名称 | 人教版B版,选修1-1,抛物线的几何性质 |

|
|
| 格式 | rar | ||
| 文件大小 | 248.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-06 21:02:53 | ||
图片预览





文档简介
(共12张PPT)
*
抛物线的几何性质
(第一课时)
*
图 形 方程 焦点 准线 范围 顶点 对称轴 e
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
y2 = 2px
(p>0)
y2 = -2px
(p>0)
x2 = 2py
(p>0)
x2 = -2py
(p>0)
x≥0
y∈R
x≤0
y∈R
y≥0
x∈R
y ≤ 0
x∈R
(0,0)
x轴
y轴
1
*
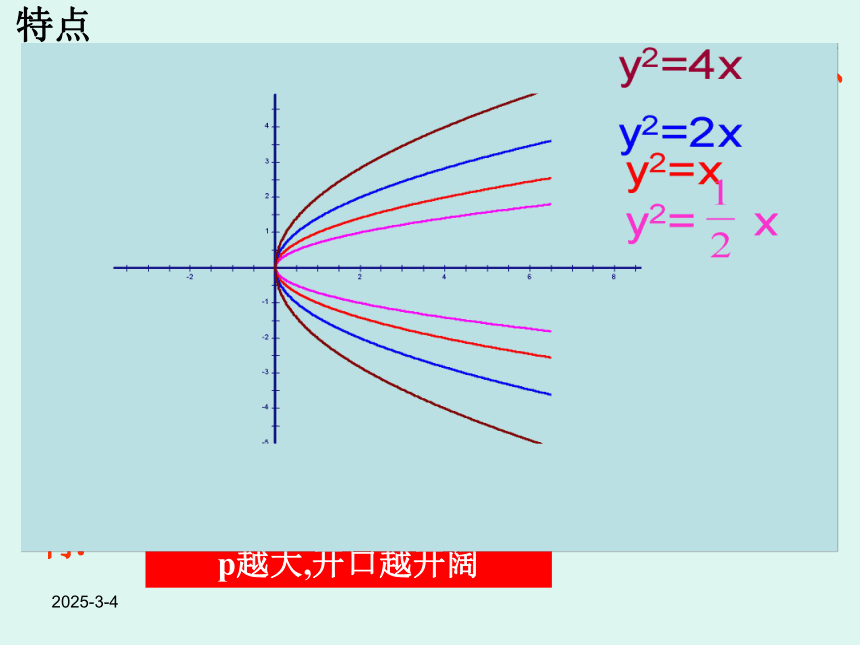
特点
1.抛物线只位于半个坐标平面内,虽然它可以无限延伸,但它没有渐近线;
2.抛物线只有一条对称轴,没有对称中心;
3.抛物线只有一个顶点、一个焦点、一条准线;
4.抛物线的离心率是确定的,为1;
5.抛物线标准方程中的p对抛物线开口的影响.
p越大,开口越开阔
*
抢答题:
求下列抛物线中x,y的取值范围,抛物线的轴,顶点坐标,焦点坐标,准线方程及开口方向.
*
例1.求下列抛物线的焦点坐标和准线方程,并指出它们的开口方向.
小试身手:
例2.已知抛物线以 轴为轴,顶点在坐标原点且开口向右,又抛物线经过点 ,求它的标准方程.
*
小结1:
1.将抛物线的方程化成标准式;
2.确定抛物线的对称轴和开口的方向(一次项定轴,符号定开口).
3.当开口方向不能确定时,注意分类讨论.
*
变式训练1
已知抛物线关于 轴对称,顶点在坐标原点,且抛物线经过点 ,求它的标准方程.
变式训练2
已知抛物线以坐标轴为轴,顶点在坐标原点,且抛物线经过点 ,求它的标准方程.
*
小结2:
1.根据已知条件确定抛物线标准方程的类型;
2.当对称轴位置不确定时,注意分类讨论:
(1)当对称轴为 轴时,可设抛物线的方程为
(2)当对称轴为 轴时,可设抛物线的方程为
*
课堂小结:
我来问,你来答;
你精彩,我点评.
*
当堂检测:
1.求下列抛物线的焦点坐标和准线方程:
2.根据下列条件,求抛物线的方程方程:
(1)顶点在原点,对称轴为x轴,且过点A(2,-4);
(2)顶点在原点,对称轴为坐标轴,且过点B(4,2).
*
当堂检测答案:
1. 焦点坐标 准线方程
(1)
(2)
(3)
(4)
*
思考题1:斜率为1的直线 经过抛物线 的焦点F,且与抛物线相交于A,B两点,求线段AB的长.
y2 = 4x
l
*
抛物线的几何性质
(第一课时)
*
图 形 方程 焦点 准线 范围 顶点 对称轴 e
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
y2 = 2px
(p>0)
y2 = -2px
(p>0)
x2 = 2py
(p>0)
x2 = -2py
(p>0)
x≥0
y∈R
x≤0
y∈R
y≥0
x∈R
y ≤ 0
x∈R
(0,0)
x轴
y轴
1
*
特点
1.抛物线只位于半个坐标平面内,虽然它可以无限延伸,但它没有渐近线;
2.抛物线只有一条对称轴,没有对称中心;
3.抛物线只有一个顶点、一个焦点、一条准线;
4.抛物线的离心率是确定的,为1;
5.抛物线标准方程中的p对抛物线开口的影响.
p越大,开口越开阔
*
抢答题:
求下列抛物线中x,y的取值范围,抛物线的轴,顶点坐标,焦点坐标,准线方程及开口方向.
*
例1.求下列抛物线的焦点坐标和准线方程,并指出它们的开口方向.
小试身手:
例2.已知抛物线以 轴为轴,顶点在坐标原点且开口向右,又抛物线经过点 ,求它的标准方程.
*
小结1:
1.将抛物线的方程化成标准式;
2.确定抛物线的对称轴和开口的方向(一次项定轴,符号定开口).
3.当开口方向不能确定时,注意分类讨论.
*
变式训练1
已知抛物线关于 轴对称,顶点在坐标原点,且抛物线经过点 ,求它的标准方程.
变式训练2
已知抛物线以坐标轴为轴,顶点在坐标原点,且抛物线经过点 ,求它的标准方程.
*
小结2:
1.根据已知条件确定抛物线标准方程的类型;
2.当对称轴位置不确定时,注意分类讨论:
(1)当对称轴为 轴时,可设抛物线的方程为
(2)当对称轴为 轴时,可设抛物线的方程为
*
课堂小结:
我来问,你来答;
你精彩,我点评.
*
当堂检测:
1.求下列抛物线的焦点坐标和准线方程:
2.根据下列条件,求抛物线的方程方程:
(1)顶点在原点,对称轴为x轴,且过点A(2,-4);
(2)顶点在原点,对称轴为坐标轴,且过点B(4,2).
*
当堂检测答案:
1. 焦点坐标 准线方程
(1)
(2)
(3)
(4)
*
思考题1:斜率为1的直线 经过抛物线 的焦点F,且与抛物线相交于A,B两点,求线段AB的长.
y2 = 4x
l
