人教版数学八年级下册 第18章 平行四边形单元测试试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学八年级下册 第18章 平行四边形单元测试试题(一)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 288.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-26 19:35:13 | ||
图片预览



文档简介
平行四边形单元测试试题(一)
一.选择题
1.如图,在Rt△ABC中,∠C=90°,AC=5,BC=12.若D,E分别为边AC,BC的中点,则DE的长为( )
A.5 B.5.5 C.6 D.6.5
2.在平面直角坐标系中,以点O(0,0),A(1,1),B(3,0)为顶点,构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( )
A.(﹣3,1) B.(4,1) C.(﹣2,1) D.(2,﹣1)
3.如图,正方形ABCD的对角线AC,BD交于点O,P为边BC上一点,且BP=OB,则∠COP的度数为( )
A.15° B.22.5° C.25° D.17.5°
4.下面关于平行四边形的说法中,不正确的是( )
A.对角线互相平分的四边形是平行四边形
B.有一组对边平行,一组对角相等的四边形是平行四边形
C.有一组对边相等,一组对角相等的四边形是平行四边形
D.有两组对角相等的四边形是平行四边形
5.如图,在平行四边形ABCD中,如果EF∥AD,GH∥CD,EF与GH相交于点O,那么图中的平行四边形一共有( )
A.4个 B.5个 C.8个 D.9个
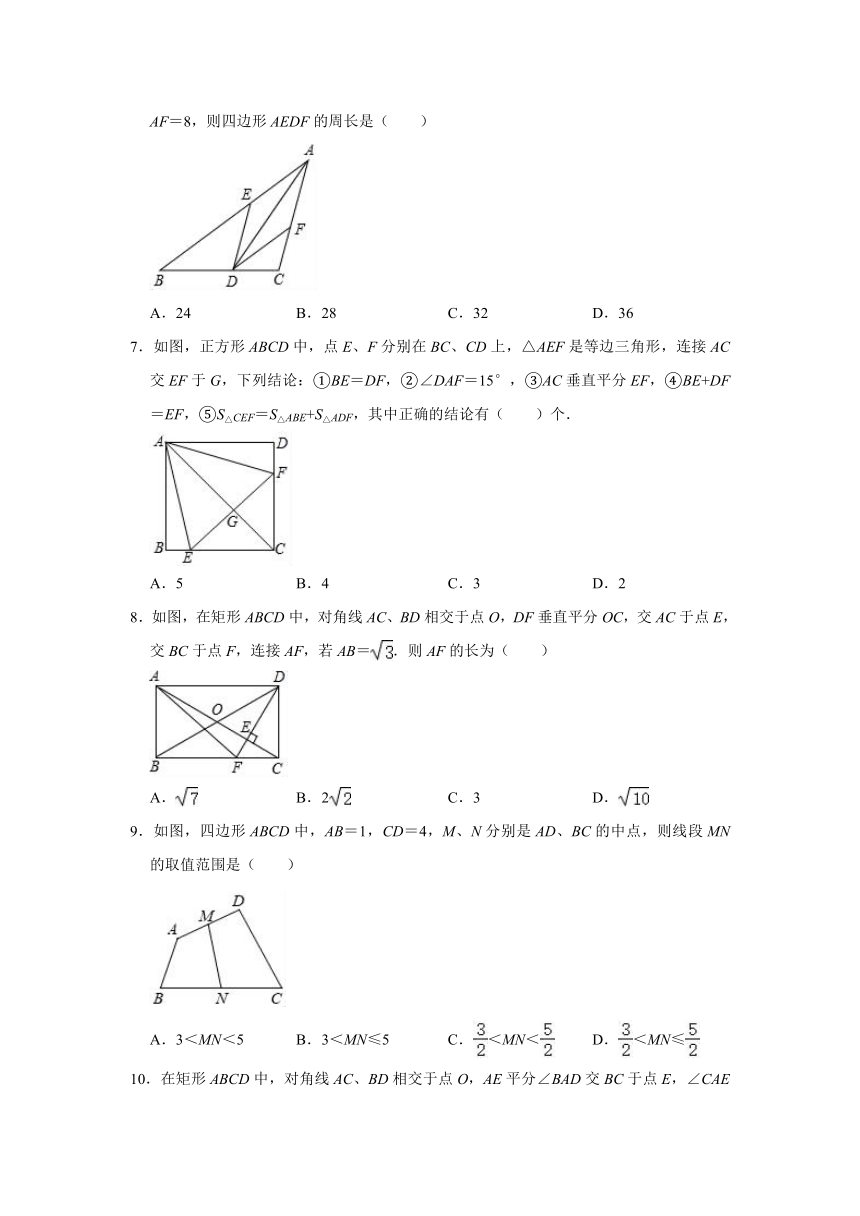
6.如图,在△ABC中,AD平分∠BAC,DE∥AC交AB于点E,DF∥AB交AC于点F,若AF=8,则四边形AEDF的周长是( )
A.24 B.28 C.32 D.36
7.如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=S△ABE+S△ADF,其中正确的结论有( )个.
A.5 B.4 C.3 D.2
8.如图,在矩形ABCD中,对角线AC、BD相交于点O,DF垂直平分OC,交AC于点E,交BC于点F,连接AF,若AB=.则AF的长为( )
A. B.2 C.3 D.
9.如图,四边形ABCD中,AB=1,CD=4,M、N分别是AD、BC的中点,则线段MN的取值范围是( )
A.3<MN<5 B.3<MN≤5 C.<MN< D.<MN≤
10.在矩形ABCD中,对角线AC、BD相交于点O,AE平分∠BAD交BC于点E,∠CAE=15°,连接OE,则下面的结论:其中正确的结论有( )
①△DOC是等边三角形;
②△BOE是等腰三角形;
③BC=2AB;
④∠AOE=150°;
⑤S△AOE=S△COE.
A.2 个 B.3个 C.4 个 D.5个
二.填空题
11.在?ABCD中,AB=5,AC=,BC边上的高为4,则BC= .
12.如图,在菱形ABCD中,对角线AC,BD相交于点O,E是AD边的中点,菱形ABCD的周长为64,则OE的长为 .
13.如图,在矩形ABCD中,AB=4,BC=8,延长BA至E,使AE=AB,以AE为边向右侧作正方形AEFG,O为正方形AEFG的中心,若过点O的一条直线平分该组合图形的面积,并分别交EF、BC于点M、N,则线段MN的长为 .
14.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=10,BD=24,则OE的长为 .
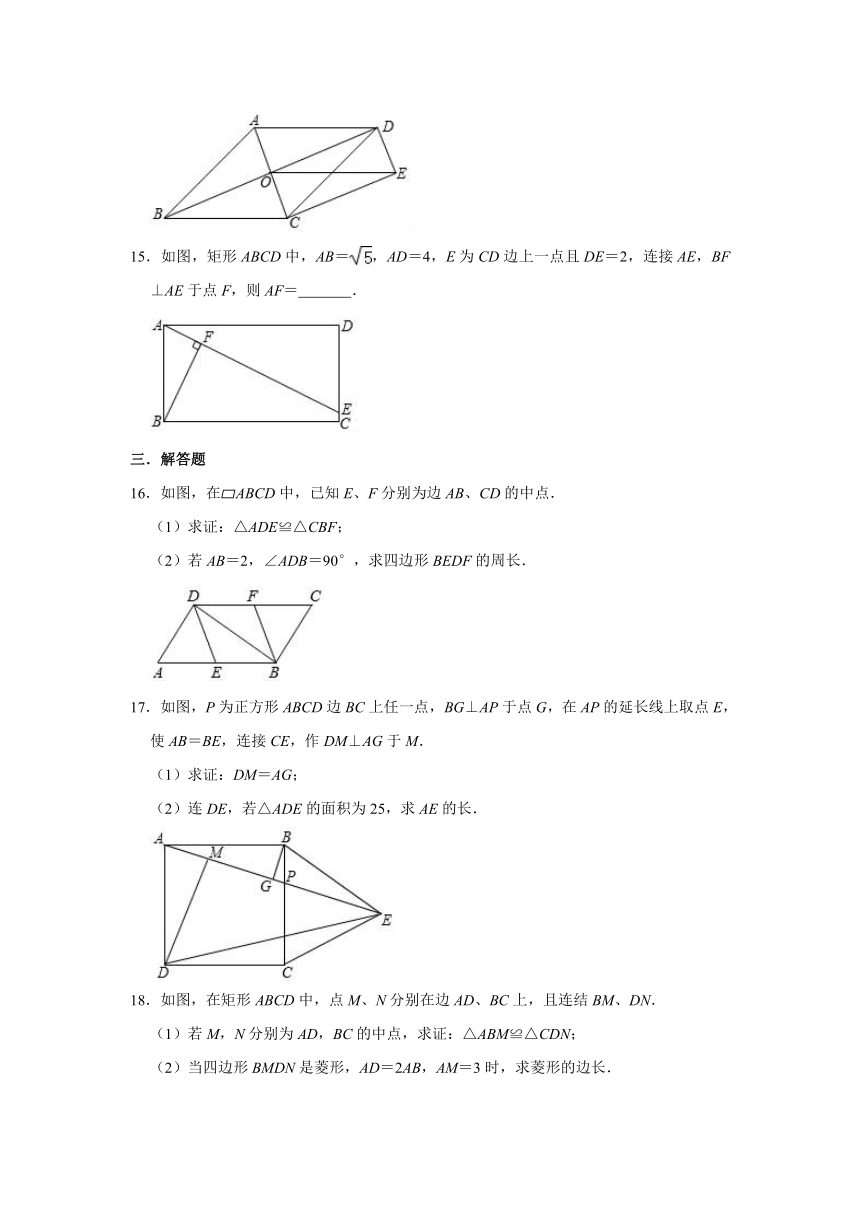
15.如图,矩形ABCD中,AB=,AD=4,E为CD边上一点且DE=2,连接AE,BF⊥AE于点F,则AF= .
三.解答题
16.如图,在?ABCD中,已知E、F分别为边AB、CD的中点.
(1)求证:△ADE≌△CBF;
(2)若AB=2,∠ADB=90°,求四边形BEDF的周长.
17.如图,P为正方形ABCD边BC上任一点,BG⊥AP于点G,在AP的延长线上取点E,使AB=BE,连接CE,作DM⊥AG于M.
(1)求证:DM=AG;
(2)连DE,若△ADE的面积为25,求AE的长.
18.如图,在矩形ABCD中,点M、N分别在边AD、BC上,且连结BM、DN.
(1)若M,N分别为AD,BC的中点,求证:△ABM≌△CDN;
(2)当四边形BMDN是菱形,AD=2AB,AM=3时,求菱形的边长.
19.在正方形ABCD中,点E是边CD的中点,点P是边AD上一点(与点A、D不重合),射线PE与BC的延长线交于点Q.
(1)如图1,求证:PE=QE;
(2)如图2,连接PB,PB=PQ,过点E作EF∥BC交PB于点F,连接AF,在不添加任何辅助线的情况下,请直接写出与线段AF相等的所有线段.
参考答案与试题解析
一.选择题
1.【解答】解:∵∠C=90°,AC=5,BC=12,
∴AB===13,
∵AD=DC,CE=EB,
∴DE=AB=6.5,
故选:D.
2.【解答】解:因为经过三点可构造三个平行四边形,即?AOBC1、?ABOC2、?AOC3B.根据平行四边形的性质,可知B、C、D正好是C1、C2、C3的坐标,
故选:A.
3.【解答】解:∵四边形ABCD是正方形,
∴∠BOC=90°,∠OBC=45°,
∵BP=OB,
∴∠BOP=∠BPO=(180°﹣45°)=67.5°,
∴∠COP=90°﹣77.5°=22.5°.
故选:B.
4.【解答】解:A、∵对角线互相平分的四边形是平行四边形,
∴选项A不符合题意;
B、∵有一组对边平行,一组对角相等的四边形是平行四边形,
∴选项B不符合题意;
C、∵有一组对边相等,一组对角相等的四边形不一定是平行四边形,
∴选项C符合题意;
D、∵有两组对角相等的四边形是平行四边形,
∴选项D不符合题意;
故选:C.
5.【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∵AD∥EF,CD∥GH,
∴AB∥GH∥CD,AD∥EF∥BC,
∴平行四边形有:?ABCD,?ABHG,?CDGH,?BCFE,?ADFE,?AGOE,?BEOH,?OFCH,?OGDF共9个.
即共有9个平行四边形,
故选:D.
6.【解答】解:∵DE∥AC,DF∥AB,
∴四边形AEDF为平行四边形,∠EAD=∠FDA,
∵AD平分∠BAC,
∴∠EAD=∠FAD=∠FDA,
∴FA=FD,
∴平行四边形AEDF为菱形.
∵AF=8,
∴C菱形AEDF=4AF=4×8=32.
故选:C.
7.【解答】解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠BCD=∠D=∠BAD=90°.
∵△AEF等边三角形,
∴AE=EF=AF,∠EAF=60°.
∴∠BAE+∠DAF=30°.
在Rt△ABE和Rt△ADF中,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,故①正确;
∵∠BAE=∠DAF,
∴∠DAF+∠DAF=30°,
即∠DAF=15°,故②正确;
∵BC=CD,
∴BC﹣BE=CD﹣DF,即CE=CF,
∵AE=AF,
∴AC垂直平分EF,故③正确;
设EC=x,由勾股定理,得EF=x,CG=x,
AG=AEsin60°=EFsin60°=2×CGsin60°=x,
∴AC=,
∴AB=,
∴BE=AB﹣x=,
∴BE+DF=x﹣x≠x,故④错误;
∵S△CEF=x2,
S△ABE=x2,
∴2S△ABE=S△CEF,
∴S△CEF=S△ABE+S△ADF,故⑤正确.
综上所述,正确的有①②③⑤,共4个.
故选:B.
8.【解答】解:∵四边形ABCD是矩形,
∴AB=CD=,AO=CO=BO=DO,
∵DF垂直平分OC,
∴OD=DC,
∴OD=DC=OC,
∴△ODC是等边三角形,
∴OD=OC=CD=,
∴AC=2,
∴BC===3,
∵△ODC是等边三角形,DE⊥AC,
∴∠CDE=∠ODE=30°,
∴DC=CF=,
∴CF=1,
∴BF=2,
∴AF===,
故选:A.
9.【解答】解:连接AC,取AC的中点H,连接MH、NH,
∵M、H分别是AD、AC的中点,
∴MH=CD=2,
同理可得,NH=AB=,
在△MHN中,MH﹣NH<MN<MH+NH,即<MN<,
当H在MN上时,MN=MH+NH=,
∴<MN≤,
故选:D.
10.【解答】解:∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴∠AEB=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,
∵∠CAE=15°,
∴∠ACE=∠AEB﹣∠CAE=45°﹣15°=30°,
∴∠BAO=90°﹣30°=60°,
∵矩形ABCD中:OA=OB=OC=OD,
∴△ABO是等边三角形,△COD是等边三角形,故①正确;
∴OB=AB,∠ABO=∠AOB=60°,
∴OB=BE,
∴△BOE是等腰三角形,故②正确;
∵∠OBE=∠ABC﹣∠ABO=90°﹣60°=30°=∠ACB,
∴∠BOE=(180°﹣30°)=75°,BC=AB,故③错误;
∴∠AOE=∠AOB+∠BOE=60°+75°=135°,故④错误;
∵AO=CO,
∴S△AOE=S△COE,故⑤正确;
故选:B.
二.填空题(共5小题)
11.【解答】解:分两种情况;
①如图1所示:
在?ABCD中,BC边上的高AE为4,AB=5,AC=2,
∴EC===2,
BE===3,
∴BC=BE+CE=3+2=5;
②如图2所示:
同①得:EC=2,AB=CD=5,BE=3,
∴BC=BE﹣EC=3﹣2=1;
综上所述,BC的长为5或1,
故答案为:5或1.
12.【解答】解:∵菱形ABCD的周长为64,
∴AB=16,
∵E为AD边中点,O为BD的中点,
∴OE=AB=8.
故答案为:8.
13.【解答】解:如图,连接AC,BD交于点H,过点O和点H的直线MN平分该组合图形的面积,交AD于S,取AE中点P,取AB中点Q,连接OP,HQ,过点O作OT⊥QH于T,
∵四边形ABCD是矩形,
∴AH=HC,
又∵Q是AB中点,
∴QH=BC=4,QH∥BC,AQ=BQ=2,
同理可求PO=AG=2,PO∥AG,EP=AP=2,
∴PO∥AD∥BC∥EF∥∥QH,EP=AP=AQ=BQ,
∴MO=OS=SH=NH,∠OPQ=∠PQH=90°,
∵OT⊥QH,
∴四边形POTQ是矩形,
∴PO=QT=2,OT=PQ=4,
∴TH=2,
∴OH===2,
∴MN=2OH=4,
故答案为:4.
14.【解答】解:∵DE∥AC,CE∥BD,
∴四边形OCED为平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=AC=5,OB=OD=BD=12,
∴∠DOC=90°,CD===13,
∴平行四边形OCED为矩形,
∴OE=CD=13,
故答案为:13.
15.【解答】解:∵四边形ABCD是矩形,
∴∠D=90°,AB∥CD,
∴∠BAF=∠AED,
由勾股定理得:AE===2,
∵BF⊥AE,
∴∠AFB=90°,
∴∠AFB=∠D,
∴△ABF∽△EAD,
∴=,
即=,
解得:AF=1,
故答案为:1.
三.解答题(共4小题)
16.【解答】证明:(1)在?ABCD中,∵AD=CB,AB=CD,∠A=∠C,
又∵E,F分别为边AB,CD的中点,
∴AE=CF,
在△ADE与△CBF中,
,
∴△ADE≌△CBF(SAS).
(2)∵∠ADB=90°,
∴△ABD,△CDB都是直角三角形,
∵AE=EB,CF=DF,
∴DE=BE=AB,BF=DF=CD,
∴DE=BE=BF=DF=1
∴四边形DEBF是菱形,周长为4.
17.【解答】解:(1)∵DM⊥AG,BG⊥AP,
∴∠AMD=∠AGB=90°.
∵∠DAM+∠GAB=90°,∠DAM+∠ADM=90°,
∴∠GAB=∠ADM.
在△ADM和△BAG中,∠AMD=∠AGB=90°,∠GAB=∠ADM,AB=AD,
∴△ADM≌△BAG(AAS).
∴DM=AG.
(2)如图所示:过点A作AF⊥BE,垂足为F.
∵△BCE是等边三角形,ABCD为正方形,
∴AB=EB,∠ABE=150°.
∴∠ABE=30°.
∴AF=AB.
设AB=BE=a,则FB=a,AB=2a,EF=(+2)a.
∵AG=GE=MD,△ADE的面积为25,
∴MDAE=MD2MD=25,解得MD=5.
∴AE=10.
18.【解答】(1)证明:∵四边形ABCD是矩形,
∴AD=BC,AB=CD,∠A=∠C=90°,
∵M,N分别为AD,BC的中点,
∴AM=CN,
在△ABM和△CDN中,
,
∴△ABM≌△CDN(SAS);
(2)设AB=x,则AD=2x,
∵四边形ABCD是矩形,
∴∠A=90°,
∵四边形BMDN是菱形,AM=3,
∴BM=DM=2x﹣3,
∵AM2+AB2=BM2,
∴32+x2=(2x﹣3)2,
解得,x1=0(舍去),x2=4,
即AB=4,
∴BM==5,
即菱形的边长是5.
19.【解答】证明:(1)∵四边形ABCD是正方形,
∴∠D=∠ECQ=90°,
∵E是CD的中点,
∴DE=CE,
又∵∠DEP=∠CEQ,
∴△PDE≌△QCE(ASA);
∴PE=QE;
(2)∵PB=PQ,
∴∠PBQ=∠Q,
∵AD∥BC,
∴∠APB=∠PBQ=∠Q=∠EPD,
∵△PDE≌△QCE,
∴PE=QE,
∴EF∥BQ,
∵PF=BF,
∴在Rt△PAB中,AF=PF=BF,
∴∠APF=∠PAF,
∴∠PAF=∠EPD,
∴PE∥AF,
∵EF∥BQ∥AD,
∴四边形AFEP是平行四边形,
∴AF=PE=EQ,
∴与线段AF相等的所有线段为BF、PF、PE、QE.
一.选择题
1.如图,在Rt△ABC中,∠C=90°,AC=5,BC=12.若D,E分别为边AC,BC的中点,则DE的长为( )
A.5 B.5.5 C.6 D.6.5
2.在平面直角坐标系中,以点O(0,0),A(1,1),B(3,0)为顶点,构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( )
A.(﹣3,1) B.(4,1) C.(﹣2,1) D.(2,﹣1)
3.如图,正方形ABCD的对角线AC,BD交于点O,P为边BC上一点,且BP=OB,则∠COP的度数为( )
A.15° B.22.5° C.25° D.17.5°
4.下面关于平行四边形的说法中,不正确的是( )
A.对角线互相平分的四边形是平行四边形
B.有一组对边平行,一组对角相等的四边形是平行四边形
C.有一组对边相等,一组对角相等的四边形是平行四边形
D.有两组对角相等的四边形是平行四边形
5.如图,在平行四边形ABCD中,如果EF∥AD,GH∥CD,EF与GH相交于点O,那么图中的平行四边形一共有( )
A.4个 B.5个 C.8个 D.9个
6.如图,在△ABC中,AD平分∠BAC,DE∥AC交AB于点E,DF∥AB交AC于点F,若AF=8,则四边形AEDF的周长是( )
A.24 B.28 C.32 D.36
7.如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=S△ABE+S△ADF,其中正确的结论有( )个.
A.5 B.4 C.3 D.2
8.如图,在矩形ABCD中,对角线AC、BD相交于点O,DF垂直平分OC,交AC于点E,交BC于点F,连接AF,若AB=.则AF的长为( )
A. B.2 C.3 D.
9.如图,四边形ABCD中,AB=1,CD=4,M、N分别是AD、BC的中点,则线段MN的取值范围是( )
A.3<MN<5 B.3<MN≤5 C.<MN< D.<MN≤
10.在矩形ABCD中,对角线AC、BD相交于点O,AE平分∠BAD交BC于点E,∠CAE=15°,连接OE,则下面的结论:其中正确的结论有( )
①△DOC是等边三角形;
②△BOE是等腰三角形;
③BC=2AB;
④∠AOE=150°;
⑤S△AOE=S△COE.
A.2 个 B.3个 C.4 个 D.5个
二.填空题
11.在?ABCD中,AB=5,AC=,BC边上的高为4,则BC= .
12.如图,在菱形ABCD中,对角线AC,BD相交于点O,E是AD边的中点,菱形ABCD的周长为64,则OE的长为 .
13.如图,在矩形ABCD中,AB=4,BC=8,延长BA至E,使AE=AB,以AE为边向右侧作正方形AEFG,O为正方形AEFG的中心,若过点O的一条直线平分该组合图形的面积,并分别交EF、BC于点M、N,则线段MN的长为 .
14.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=10,BD=24,则OE的长为 .
15.如图,矩形ABCD中,AB=,AD=4,E为CD边上一点且DE=2,连接AE,BF⊥AE于点F,则AF= .
三.解答题
16.如图,在?ABCD中,已知E、F分别为边AB、CD的中点.
(1)求证:△ADE≌△CBF;
(2)若AB=2,∠ADB=90°,求四边形BEDF的周长.
17.如图,P为正方形ABCD边BC上任一点,BG⊥AP于点G,在AP的延长线上取点E,使AB=BE,连接CE,作DM⊥AG于M.
(1)求证:DM=AG;
(2)连DE,若△ADE的面积为25,求AE的长.
18.如图,在矩形ABCD中,点M、N分别在边AD、BC上,且连结BM、DN.
(1)若M,N分别为AD,BC的中点,求证:△ABM≌△CDN;
(2)当四边形BMDN是菱形,AD=2AB,AM=3时,求菱形的边长.
19.在正方形ABCD中,点E是边CD的中点,点P是边AD上一点(与点A、D不重合),射线PE与BC的延长线交于点Q.
(1)如图1,求证:PE=QE;
(2)如图2,连接PB,PB=PQ,过点E作EF∥BC交PB于点F,连接AF,在不添加任何辅助线的情况下,请直接写出与线段AF相等的所有线段.
参考答案与试题解析
一.选择题
1.【解答】解:∵∠C=90°,AC=5,BC=12,
∴AB===13,
∵AD=DC,CE=EB,
∴DE=AB=6.5,
故选:D.
2.【解答】解:因为经过三点可构造三个平行四边形,即?AOBC1、?ABOC2、?AOC3B.根据平行四边形的性质,可知B、C、D正好是C1、C2、C3的坐标,
故选:A.
3.【解答】解:∵四边形ABCD是正方形,
∴∠BOC=90°,∠OBC=45°,
∵BP=OB,
∴∠BOP=∠BPO=(180°﹣45°)=67.5°,
∴∠COP=90°﹣77.5°=22.5°.
故选:B.
4.【解答】解:A、∵对角线互相平分的四边形是平行四边形,
∴选项A不符合题意;
B、∵有一组对边平行,一组对角相等的四边形是平行四边形,
∴选项B不符合题意;
C、∵有一组对边相等,一组对角相等的四边形不一定是平行四边形,
∴选项C符合题意;
D、∵有两组对角相等的四边形是平行四边形,
∴选项D不符合题意;
故选:C.
5.【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∵AD∥EF,CD∥GH,
∴AB∥GH∥CD,AD∥EF∥BC,
∴平行四边形有:?ABCD,?ABHG,?CDGH,?BCFE,?ADFE,?AGOE,?BEOH,?OFCH,?OGDF共9个.
即共有9个平行四边形,
故选:D.
6.【解答】解:∵DE∥AC,DF∥AB,
∴四边形AEDF为平行四边形,∠EAD=∠FDA,
∵AD平分∠BAC,
∴∠EAD=∠FAD=∠FDA,
∴FA=FD,
∴平行四边形AEDF为菱形.
∵AF=8,
∴C菱形AEDF=4AF=4×8=32.
故选:C.
7.【解答】解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠BCD=∠D=∠BAD=90°.
∵△AEF等边三角形,
∴AE=EF=AF,∠EAF=60°.
∴∠BAE+∠DAF=30°.
在Rt△ABE和Rt△ADF中,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,故①正确;
∵∠BAE=∠DAF,
∴∠DAF+∠DAF=30°,
即∠DAF=15°,故②正确;
∵BC=CD,
∴BC﹣BE=CD﹣DF,即CE=CF,
∵AE=AF,
∴AC垂直平分EF,故③正确;
设EC=x,由勾股定理,得EF=x,CG=x,
AG=AEsin60°=EFsin60°=2×CGsin60°=x,
∴AC=,
∴AB=,
∴BE=AB﹣x=,
∴BE+DF=x﹣x≠x,故④错误;
∵S△CEF=x2,
S△ABE=x2,
∴2S△ABE=S△CEF,
∴S△CEF=S△ABE+S△ADF,故⑤正确.
综上所述,正确的有①②③⑤,共4个.
故选:B.
8.【解答】解:∵四边形ABCD是矩形,
∴AB=CD=,AO=CO=BO=DO,
∵DF垂直平分OC,
∴OD=DC,
∴OD=DC=OC,
∴△ODC是等边三角形,
∴OD=OC=CD=,
∴AC=2,
∴BC===3,
∵△ODC是等边三角形,DE⊥AC,
∴∠CDE=∠ODE=30°,
∴DC=CF=,
∴CF=1,
∴BF=2,
∴AF===,
故选:A.
9.【解答】解:连接AC,取AC的中点H,连接MH、NH,
∵M、H分别是AD、AC的中点,
∴MH=CD=2,
同理可得,NH=AB=,
在△MHN中,MH﹣NH<MN<MH+NH,即<MN<,
当H在MN上时,MN=MH+NH=,
∴<MN≤,
故选:D.
10.【解答】解:∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴∠AEB=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,
∵∠CAE=15°,
∴∠ACE=∠AEB﹣∠CAE=45°﹣15°=30°,
∴∠BAO=90°﹣30°=60°,
∵矩形ABCD中:OA=OB=OC=OD,
∴△ABO是等边三角形,△COD是等边三角形,故①正确;
∴OB=AB,∠ABO=∠AOB=60°,
∴OB=BE,
∴△BOE是等腰三角形,故②正确;
∵∠OBE=∠ABC﹣∠ABO=90°﹣60°=30°=∠ACB,
∴∠BOE=(180°﹣30°)=75°,BC=AB,故③错误;
∴∠AOE=∠AOB+∠BOE=60°+75°=135°,故④错误;
∵AO=CO,
∴S△AOE=S△COE,故⑤正确;
故选:B.
二.填空题(共5小题)
11.【解答】解:分两种情况;
①如图1所示:
在?ABCD中,BC边上的高AE为4,AB=5,AC=2,
∴EC===2,
BE===3,
∴BC=BE+CE=3+2=5;
②如图2所示:
同①得:EC=2,AB=CD=5,BE=3,
∴BC=BE﹣EC=3﹣2=1;
综上所述,BC的长为5或1,
故答案为:5或1.
12.【解答】解:∵菱形ABCD的周长为64,
∴AB=16,
∵E为AD边中点,O为BD的中点,
∴OE=AB=8.
故答案为:8.
13.【解答】解:如图,连接AC,BD交于点H,过点O和点H的直线MN平分该组合图形的面积,交AD于S,取AE中点P,取AB中点Q,连接OP,HQ,过点O作OT⊥QH于T,
∵四边形ABCD是矩形,
∴AH=HC,
又∵Q是AB中点,
∴QH=BC=4,QH∥BC,AQ=BQ=2,
同理可求PO=AG=2,PO∥AG,EP=AP=2,
∴PO∥AD∥BC∥EF∥∥QH,EP=AP=AQ=BQ,
∴MO=OS=SH=NH,∠OPQ=∠PQH=90°,
∵OT⊥QH,
∴四边形POTQ是矩形,
∴PO=QT=2,OT=PQ=4,
∴TH=2,
∴OH===2,
∴MN=2OH=4,
故答案为:4.
14.【解答】解:∵DE∥AC,CE∥BD,
∴四边形OCED为平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=AC=5,OB=OD=BD=12,
∴∠DOC=90°,CD===13,
∴平行四边形OCED为矩形,
∴OE=CD=13,
故答案为:13.
15.【解答】解:∵四边形ABCD是矩形,
∴∠D=90°,AB∥CD,
∴∠BAF=∠AED,
由勾股定理得:AE===2,
∵BF⊥AE,
∴∠AFB=90°,
∴∠AFB=∠D,
∴△ABF∽△EAD,
∴=,
即=,
解得:AF=1,
故答案为:1.
三.解答题(共4小题)
16.【解答】证明:(1)在?ABCD中,∵AD=CB,AB=CD,∠A=∠C,
又∵E,F分别为边AB,CD的中点,
∴AE=CF,
在△ADE与△CBF中,
,
∴△ADE≌△CBF(SAS).
(2)∵∠ADB=90°,
∴△ABD,△CDB都是直角三角形,
∵AE=EB,CF=DF,
∴DE=BE=AB,BF=DF=CD,
∴DE=BE=BF=DF=1
∴四边形DEBF是菱形,周长为4.
17.【解答】解:(1)∵DM⊥AG,BG⊥AP,
∴∠AMD=∠AGB=90°.
∵∠DAM+∠GAB=90°,∠DAM+∠ADM=90°,
∴∠GAB=∠ADM.
在△ADM和△BAG中,∠AMD=∠AGB=90°,∠GAB=∠ADM,AB=AD,
∴△ADM≌△BAG(AAS).
∴DM=AG.
(2)如图所示:过点A作AF⊥BE,垂足为F.
∵△BCE是等边三角形,ABCD为正方形,
∴AB=EB,∠ABE=150°.
∴∠ABE=30°.
∴AF=AB.
设AB=BE=a,则FB=a,AB=2a,EF=(+2)a.
∵AG=GE=MD,△ADE的面积为25,
∴MDAE=MD2MD=25,解得MD=5.
∴AE=10.
18.【解答】(1)证明:∵四边形ABCD是矩形,
∴AD=BC,AB=CD,∠A=∠C=90°,
∵M,N分别为AD,BC的中点,
∴AM=CN,
在△ABM和△CDN中,
,
∴△ABM≌△CDN(SAS);
(2)设AB=x,则AD=2x,
∵四边形ABCD是矩形,
∴∠A=90°,
∵四边形BMDN是菱形,AM=3,
∴BM=DM=2x﹣3,
∵AM2+AB2=BM2,
∴32+x2=(2x﹣3)2,
解得,x1=0(舍去),x2=4,
即AB=4,
∴BM==5,
即菱形的边长是5.
19.【解答】证明:(1)∵四边形ABCD是正方形,
∴∠D=∠ECQ=90°,
∵E是CD的中点,
∴DE=CE,
又∵∠DEP=∠CEQ,
∴△PDE≌△QCE(ASA);
∴PE=QE;
(2)∵PB=PQ,
∴∠PBQ=∠Q,
∵AD∥BC,
∴∠APB=∠PBQ=∠Q=∠EPD,
∵△PDE≌△QCE,
∴PE=QE,
∴EF∥BQ,
∵PF=BF,
∴在Rt△PAB中,AF=PF=BF,
∴∠APF=∠PAF,
∴∠PAF=∠EPD,
∴PE∥AF,
∵EF∥BQ∥AD,
∴四边形AFEP是平行四边形,
∴AF=PE=EQ,
∴与线段AF相等的所有线段为BF、PF、PE、QE.
