安徽省蚌埠市2020-2021学年第一学期期末教学质量检测九年级数学试题卷(PDF版 含答案)
文档属性
| 名称 | 安徽省蚌埠市2020-2021学年第一学期期末教学质量检测九年级数学试题卷(PDF版 含答案) |  | |
| 格式 | |||
| 文件大小 | 801.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-26 22:06:38 | ||
图片预览




文档简介
蚌 埠 市 2 0 2 0 — 2 0 2 1 学 年 度 第 一 学 期 期 末 教 学 质 量 监 测
九 年 级 数 学 ( 沪 科 版 )
考 试 时 间 : 1 2 0 分 钟 满 分 : 1 5 0 分
一 、 选 择 题 : ( 本 大 题 共 1 0 小 题 , 每 小 题 4 分 , 共 4 0 分 , 在 每 小 题 给 出 的 A , B , C , D 四 个 选 项 中 , 只 有
一 项 是 符 合 题 目 要 求 的 , 请 在 答 题 卷 上 将 正 确 答 案 的 字 母 代 号 涂 黑 )
2
1 ? 将 抛 物 线 y = 2 x + 1 向 右 平 移 2 个 单 位 , 再 向 下 平 移 3 个 单 位 , 则 平 移 后 的 抛 物 线 解 析 式 为
2 2
A ? y = 2 x + 3 B ? y = 2 ( x - 2 ) - 2
2 2
C ? y = 2 ( x + 2 ) - 2 D ? y = 2 ( x + 2 ) + 4
2 ? 在 直 角 坐 标 平 面 内 有 一 点 P ( 3 , 4 ) , O P 与 x 轴 正 半 轴 的 夹 角 为 α , 则 s in α 的 值 是
3 4 3 4
A ? B ? C ? D ?
4 3 5 5
3 ? 如 图 , 已 知 ∠ 1 = ∠ 2 , 则 添 加 下 列 一 个 条 件 后 , 仍 无 法 判 定 △ A B C ∽ △ A D E 的 是
A B B C A B A C
A ? = B ? = C ? ∠ B = ∠ A D E D ? ∠ C = ∠ E
A D D E A D A E
第 3 题 图 第 5 题 图 第 6 题 图
2
4 ? 已 知 点 A ( - 3 , y 1 ) , B ( 1 , y 2 ) 在 二 次 函 数 y = - ( x + 2 ) + m 的 图 象 上 , 则 y 1 , y 2 的 大 小 关
系 是
A ? y 1 < y 2 B ? y 1 > y 2 C ? y 1 = y 2 D ? 不 能 确 定
5 ? 如 图 , 四 边 形 A B C D 内 接 于 ⊙ O , 已 知 ∠ A D C = 1 4 0 ° , 则 ∠ A O C 的 大 小 是
A ? 8 0 ° B ? 7 0 ° C ? 6 0 ° D ? 4 0 °
S △ A B E
6 ? 如 图 , 将 一 副 三 角 尺 如 图 所 示 叠 放 在 一 起 , 其 中 ∠ B A C = ∠ A C D = 9 0 ° , 则 的 值 是
S △ D C E
1 1
A ? 3 B ? C ? 2 D ?
3 4
蚌 埠 市 九 年 级 数 学 试 卷 第 1 页 ( 共 6 页 )
书书书
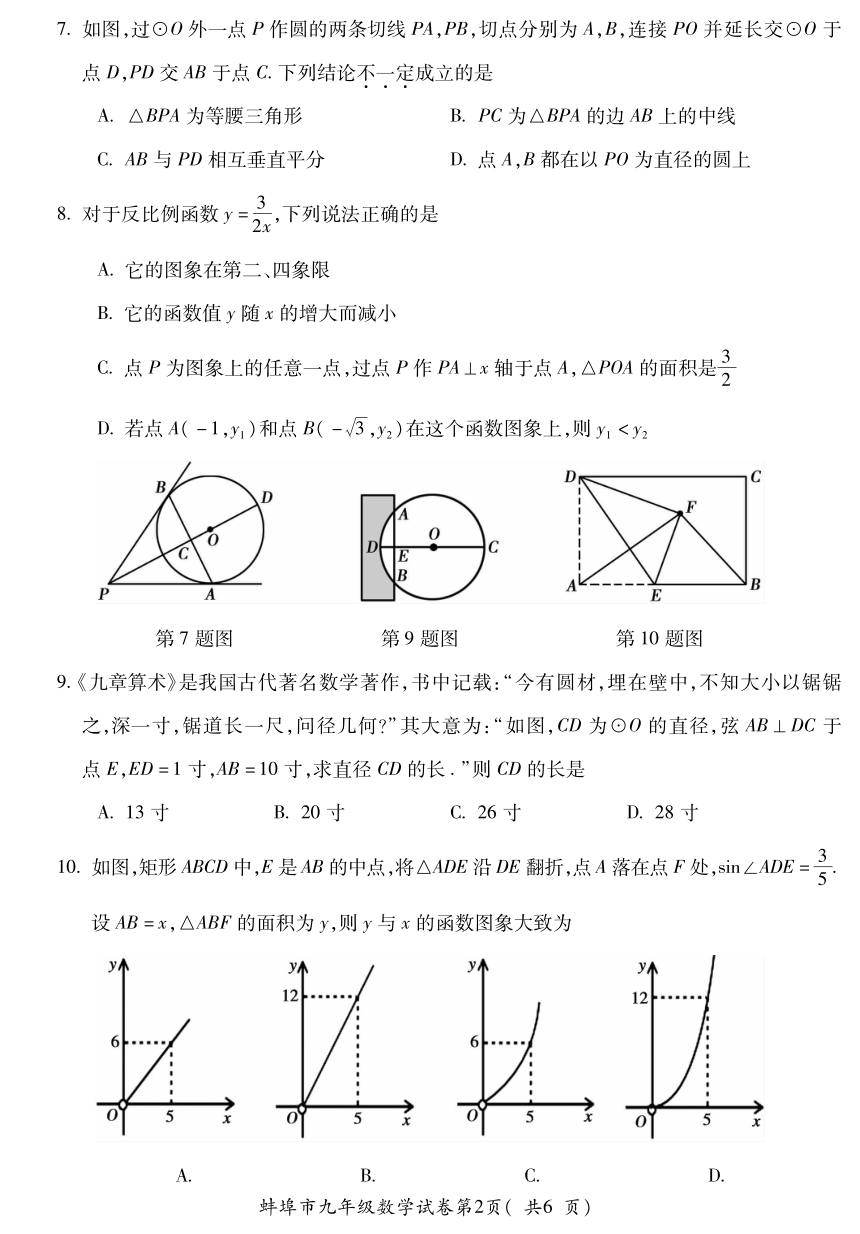
7 ? 如 图 , 过 ⊙ O 外 一 点 P 作 圆 的 两 条 切 线 P A , P B , 切 点 分 别 为 A , B , 连 接 P O 并 延 长 交 ⊙ O 于
点 D , P D 交 A B 于 点 C . 下 列 结 论 不 一 定 成 立 的 是
獉 獉 獉
A ? △ B P A 为 等 腰 三 角 形 B ? P C 为 △ B P A 的 边 A B 上 的 中 线
C ? A B 与 P D 相 互 垂 直 平 分 D ? 点 A , B 都 在 以 P O 为 直 径 的 圆 上
3
8 ? 对 于 反 比 例 函 数 y = , 下 列 说 法 正 确 的 是
2 x
A ? 它 的 图 象 在 第 二 、 四 象 限
B ? 它 的 函 数 值 y 随 x 的 增 大 而 减 小
3
C ? 点 P 为 图 象 上 的 任 意 一 点 , 过 点 P 作 P A ⊥ x 轴 于 点 A , △ P O A 的 面 积 是 2
D ? 若 点 A ( - 1 , y 1 ) 和 点 B ( -
槡 3 , y 2 ) 在 这 个 函 数 图 象 上 , 则 y 1 < y 2
第 7 题 图 第 9 题 图 第 1 0 题 图
9 ? 《 九 章 算 术 》 是 我 国 古 代 著 名 数 学 著 作 , 书 中 记 载 : “ 今 有 圆 材 , 埋 在 壁 中 , 不 知 大 小 以 锯 锯
之 , 深 一 寸 , 锯 道 长 一 尺 , 问 径 几 何 ? ” 其 大 意 为 : “ 如 图 , C D 为 ⊙ O 的 直 径 , 弦 A B ⊥ D C 于
点 E , E D = 1 寸 , A B = 1 0 寸 , 求 直 径 C D 的 长 ? ” 则 C D 的 长 是
A ? 1 3 寸 B ? 2 0 寸 C ? 2 6 寸 D ? 2 8 寸
3
1 0 ? 如 图 , 矩 形 A B C D 中 , E 是 A B 的 中 点 , 将 △ A D E 沿 D E 翻 折 , 点 A 落 在 点 F 处 , s in ∠ A D E = ?
5
设 A B = x , △ A B F 的 面 积 为 y , 则 y 与 x 的 函 数 图 象 大 致 为
A ? B ? C ? D ?
蚌 埠 市 九 年 级 数 学 试 卷 第 2 页 ( 共 6 页 )
二 、 填 空 题 : ( 本 大 题 共 4 个 小 题 , 每 小 题 5 分 , 共 2 0 分 , 请 将 答 案 直 接 填 在 题 中 的 横 线 上 )
2
1 1 ? 抛 物 线 y = 2 x - 4 x + 4 的 顶 点 坐 标 为 ?
)
1 2 ? 如 图 , 在 6 × 6 的 正 方 形 网 格 中 , ⊙ O 经 过 格 点 A , B , C , 点 P 是 A C B 上 任 意 一 点 , 连 接 A P ,
B P , 则 ta n ∠ A P B 的 值 为 ?
1 3 ? 如 图 , 一 块 含 有 3 0 ° 角 的 直 角 三 角 板 A B C , 在 水 平 桌 面 上 绕 点 C 按 顺 时 针 方 向 旋 转 到 三 角
板 A ′ B ′ C ′ 的 位 置 , 若 A C = 3 c m , 则 顶 点 A 在 旋 转 过 程 中 所 经 过 的 路 径 长 为 c m ?
1 4 ? 如 图 , 在 R t △ A B C 中 , ∠ A C B = 9 0 ° , A C = 4 , B C = 6 , 点 D 是 边 B C 的 中 点 , 点 E 是 边 A B 上 的
任 意 一 点 ( 点 E 不 与 点 B 重 合 ) , 沿 D E 翻 折 △ D B E , 使 点 B 落 在 △ A B C 所 在 平 面 内 点 F
处 , 连 接 A F ?
( 1 ) 当 D E ⊥ B D 时 , D E 的 长 度 为 ;
( 2 ) 当 线 段 A F 的 长 取 最 小 值 时 , ta n ∠ F B D 的 值 为 ?
第 1 2 题 图 第 1 3 题 图 第 1 4 题 图
三 、 ( 本 题 共 两 小 题 , 每 小 题 8 分 , 共 1 6 分 )
2
1 5 ? 计 算 : s in 4 5 ° + c o s 3 0 ° · ta n 6 0 ° .
a + 4 b + 3 c + 8
1 6 ? 已 知 a , b , c 是 △ A B C 的 三 边 , 满 足 = = , 且 a + b + c = 1 2 .
3 2 4
( 1 ) 求 a , b , c 的 值 ;
( 2 ) 若 线 段 x 是 线 段 a , b 的 比 例 中 项 , 求 x ?
蚌 埠 市 九 年 级 数 学 试 卷 第 3 页 ( 共 6 页 )
四 、 ( 本 题 共 两 小 题 , 每 小 题 8 分 , 共 1 6 分 )
1 7 ? 如 图 , 在 平 面 直 角 坐 标 系 中 , 点 A , B 的 坐 标 分 别 为 ( 1 , 3 ) , ( 3 , 2 ) ?
第 1 7 题 图
( 1 ) 画 出 △ O A B 绕 点 B 顺 时 针 旋 转 9 0 ° 后 的 △ O ′ A ′ B ;
( 2 ) 以 点 B 为 位 似 中 心 , 相 似 比 为 2 ∶1 , 在 x 轴 的 上 方 画 出 △ O ′ A ′ B 放 大 后 的 △ O ″ A ″ B ;
( 3 ) 点 M 是 O A 的 中 点 , 在 ( 1 ) 和 ( 2 ) 的 变 换 下 , M 的 对 应 点 M ″ 的 坐 标 为 .
1 8 ? 为 进 一 步 加 强 疫 情 防 控 工 作 , 某 学 校 决 定 安 装 红 外 线 体 温 监 测 仪 , 该 设 备 通 过 探 测 人 体 红
外 辐 射 能 量 对 进 入 测 温 区 域 的 人 员 进 行 快 速 测 温 , 无 需 人 员 停 留 和 接 触 , 安 装 示 意 图 如
下 . 已 知 检 测 仪 探 测 线 与 地 面 A C 形 成 的 最 大 角 ∠ O B C = 7 5 ° , 最 小 角 ∠ O A C = 3 0 ° , 本 设 备
需 安 装 在 垂 直 于 水 平 地 面 A C 的 支 架 C P 上 ? 现 学 校 要 求 测 温 区 域 的 宽 度 A B 为 4 m , 请 你
帮 助 学 校 确 定 该 设 备 的 安 装 高 度 O C . ( 结 果 保 留 根 号 )
第 1 8 题 图
蚌 埠 市 九 年 级 数 学 试 卷 第 4 页 ( 共 6 页 )
五 、 ( 本 题 共 两 小 题 , 每 小 题 1 0 分 , 共 2 0 分 ) k
1 9 ? 如 图 , 在 平 面 直 角 坐 标 系 中 , 正 比 例 函 数 y = 3 x 与 反 比 例 函 数 y = ( k > 0 ) 的 图 象 交 于 A ,
x
B 两 点 , 点 A 的 横 坐 标 为 2 , A C ⊥ x 轴 , 垂 足 为 C , 连 接 B C .
( 1 ) 反 比 例 函 数 的 表 达 式 为 ; k
( 2 ) 正 比 例 函 数 y = 3 x 的 值 大 于 反 比 例 函 数 y = 的 值 时 x 的
x
取 值 范 围 是 ;
( 3 ) 求 △ A B C 的 面 积 .
第 1 9 题 图
2 0 ? 如 图 , B 为 ⊙ O 上 一 点 , A 为 ⊙ O 外 一 点 , 连 接 A B , A O , 线 段 A O 交 ⊙ O 于 点 C , A O 的 延 长 线
) 1
交 ⊙ O 于 点 D , E 是 B C D 上 不 与 B , D 重 合 的 点 , s in A = , ∠ B E D = 6 0 ° .
2
( 1 ) 求 证 : A B 是 ⊙ O 的 切 线 ;
( 2 ) 过 D 点 作 ⊙ O 的 切 线 D F , 交 A B 延 长 线 于 点 F , 若
D F = 3
槡 3 , 求 ⊙ O 的 半 径 ?
第 2 0 题 图
六 、 ( 本 题 满 分 1 2 分 )
2 1 ? 如 图 1 , 在 △ A B C 中 , A B = 4
槡 2 , ∠ B = 4 5 ° , ∠ C = 6 0 ° ?
( 1 ) 求 B C 边 上 的 高 线 长 ;
( 2 ) 如 图 2 , 若 点 E 为 线 段 A B 的 中 点 , 点 F 在 边 A C 上 , 连 接 E F , 沿 E F 将 △ A E F 折 叠 得 到
△ P E F ? 连 接 A P , 当 P F ⊥ A C 时 , 求 P F 的 长 ?
第 2 1 题 图
蚌 埠 市 九 年 级 数 学 试 卷 第 5 页 ( 共 6 页 )
七 、 ( 本 题 满 分 1 2 分 )
2 2 ? 某 大 学 生 利 用 暑 假 4 0 天 社 会 实 践 参 与 了 一 家 网 店 经 营 , 了 解 到 一 种 新 型 商 品 成 本 为 2 0
元 / 件 , 第 x 天 销 售 量 为 p 件 , 销 售 单 价 为 q 元 ? 经 跟 踪 调 查 发 现 , 这 4 0 天 中 p - 5 0 与 x 成
正 比 , 前 2 0 天 ( 包 含 第 2 0 天 ) , q 与 x 的 关 系 满 足 关 系 式 q = 3 0 + a x ; 从 第 2 1 天 到 第 4 0 天
中 , q 是 基 础 价 与 浮 动 价 的 和 , 其 中 基 础 价 保 持 不 变 , 浮 动 价 与 x 成 反 比 , 且 得 到 了 表 中 的
数 据 :
x ( 天 ) 1 0 2 1 3 5
q ( 元 / 件 ) 3 5 4 5 3 5
p ( 件 ) 4 0
( 1 ) 请 直 接 写 出 a 的 值 为 , 直 接 写 出 这 4 0 天 中 p 与 x 的 关 系 式 为 ;
( 2 ) 从 第 2 1 天 到 第 4 0 天 中 , 求 q 与 x 满 足 的 关 系 式 ;
( 3 ) 求 这 4 0 天 里 该 网 店 第 几 天 获 得 的 利 润 最 大 ? 最 大 为 多 少 ?
八 、 ( 本 题 满 分 1 4 分 )
2 3 ? 矩 形 A B C D 中 , A B = 6 , A D = 8 , 点 P 是 对 角 线 A C 上 一 动 点 ( 不 与 A , C 重 合 ) , 过 点 P 作 E F
⊥ B C , 分 别 交 A D , B C 于 点 E , F ?
( 1 ) 如 图 1 , 若 E 为 A D 的 黄 金 分 割 点 ( A E < D E ) , 求 A P 的 长 ;
( 2 ) 如 图 2 , 连 结 P D , 作 P M ⊥ P D , 交 射 线 B C 于 点 M , 以 线 段 P D , P M 为 邻 边 作 矩 形
P M N D .
P M
① 求 的 值 ;
P D
② 求 矩 形 P M N D 的 面 积 最 小 值 .
第 2 3 题 图
蚌 埠 市 九 年 级 数 学 试 卷 第 6 页 ( 共 6 页 )
蚌 埠 市 2 0 2 0 — 2 0 2 1 学 年 度 第 一 学 期 期 末 教 学 质 量 监 测
九 年 级 数 学 ( 沪 科 版 ) 参 考 答 案 及 评 分 标 准
一 、 选 择 题
题 号 1 2 3 4 5 6 7 8 9 1 0
答 案 B D A B A B C D C C
二 、 填 空 题 1 1
1 1 ? ( 1 , 2 ) 1 2 ? 1 3 ? 2 π 1 4 ? ( 1 ) 2 ( 2 )
2 2
三 、 解 答 题
2 2 3 1 3
1 5 ? 解 : 原 式 = ( 槡 ) + 槡 × 3 = + = 2 ? … … … … … … … … … … … … … … … … … … 8 分
2 2 槡 2 2
a + 4 b + 3 c + 8
1 6 ? ( 1 ) ∵ = = , 且 a + b + c = 1 2 ,
3 2 4
a + 4 b + 3 c + 8 a + 4 + b + 3 + c + 8 a + b + c + 1 5 1 2 + 1 5
∴ = = = = = = 3 ,
3 2 4 3 + 2 + 4 9 9
a + 4 b + 3 c + 8
∴ = 3 , = 3 , = 3 ,
3 2 4
∴ a = 5 , b = 3 , c = 4 ; … … … … … … … … … … … … … … … … … … … … … … … … … … 4 分
( 2 ) ∵ 线 段 x 是 线 段 a 、 b 的 比 例 中 项 ,
2
∴ x = 3 × 5 = 1 5 ,
∴ x =
槡 1 5 ( x = -
槡 1 5 舍 去 ) . … … … … … … … … … … … … … … … … … … … … … 8 分
1 7 ? ( 1 ) 如 图 , △ O ′ A ′ B 即 为 所 求 ; … … … … … … … … … … … … … … … … … … … … … … … 3 分
( 2 ) 如 图 , △ O ″ A ″ B 即 为 所 求 ; … … … … … … … … … … … … … … … … … … … … … … … 6 分
( 3 ) ( 2 , 7 ) ? … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … 8 分
蚌 埠 市 九 年 级 数 学 参 考 答 案 第 1 页 ( 共 4 页 )
1 8 ? 解 : 根 据 题 意 可 知 : O C ⊥ A C , ∠ O B C = 7 5 ° , ∠ O A C = 3 0 ° , A B = 4 m ,
过 B 点 作 B D ⊥ O A , 垂 足 为 D , 则 ∠ D B O = ∠ D O B = 4 5 ° , … … … … … … … … … … … … 2 分
且 在 R t △ A B D 中 , B D = 2 , A D = 2
槡 3 , … … … … … … … … … … … … … … … … … … … … 4 分
在 R t △ O B D 中 , O D = B D = 2 ,
∴ O A = A D + O D = 2
槡 3 + 2 , … … … … … … … … … … … … … … … … … … … … … … … … 6 分
1
在 R t △ O A C 中 , O C = O A = 3 + 1 ,
2 槡
答 : 该 设 备 的 安 装 高 度 O C 为 ( 槡 3 + 1 ) m ? … … … … … … … … … … … … … … … … … … 8 分
1 2
1 9 ? ( 1 ) y = ; … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … 3 分
x
( 2 ) - 2 < x < 0 或 x > 2 ; … … … … … … … … … … … … … … … … … … … … … … … … … 6 分
( 3 ) ∵ A 点 横 坐 标 2 , y = 2 × 3 = 6 .
∴ A 点 坐 标 为 ( 2 , 6 )
∵ A , B 关 于 原 点 对 称 ,
∴ B 点 坐 标 为 ( - 2 , - 6 ) ,
∴ B 到 O C 的 距 离 为 6 , 1
∴ S △ A B C = S △ A O C + S △ B O C = 2 S △ A O C = × 2 × 6 × 2 = 1 2 . … … … … … … … … … … … 1 0 分
2
2 0 ? ( 1 ) 证 明 : 连 接 O B , 如 图 1 ,
∵ ∠ B E D = 6 0 °
∴ ∠ B O D = 2 ∠ B E D = 1 2 0 ° ;
∴ ∠ A O B = 6 0 ° ,
1
∵ s in A = ,
2 图 1
∴ ∠ A = 3 0 ° ,
∴ ∠ A B O = 9 0 ° , 即 A B ⊥ O B ,
∴ A B 是 ⊙ O 的 切 线 ; … … … … … … … … … … … … … … … … … … … … … … … … … 5 分
( 2 ) 解 : 连 接 O F , O B , 如 图 2 ,
∵ D F , A B 是 ⊙ O 的 切 线 ,
∴ ∠ O D F = ∠ O B F = 9 0 ° ,
∵ O F = O F , O B = O D ,
∴ △ B O F ≌ △ D O F ( H L ) , 图 2
∴ ∠ B O F = ∠ D O F = 6 0 ° ,
在 R t △ D O F 中 , ∠ D O F = 6 0 ° , D F = 3
槡 3 ,
D F 3 3
∴ O D = = 槡 = 3 ,
ta n ∠ D O F
槡 3
蚌 埠 市 九 年 级 数 学 参 考 答 案 第 2 页 ( 共 4 页 )
∴ ⊙ O 的 半 径 为 3 ? … … … … … … … … … … … … … … … … … … … … … … … … … 1 0 分
2 1 ? ( 1 ) 作 A D ⊥ B C 于 D .
2
在 R t △ A B D 中 , A D = A B · s in 4 5 ° = 4
槡 2 × 槡 = 4 . … … … … … … … … … … … … … 4 分
2
( 2 ) 由 题 意 , ∠ B A C = 7 5 ° ,
又 P F ⊥ A C 时 , ∠ A F E = 4 5 ° ,
∴ ∠ A E F = 6 0 ° . … … … … … … … … … … … … … … … … … … … … … … … … … … … 6 分
易 知 A E = 2
槡 2 ,
设 A P 交 E F 于 点 G , 则 ∠ A G E = 9 0 ° ,
∴ E G =
槡 2 , A G =
槡 6 … … … … … … … … … … … … … … … … … … … … … … … … … … 8 分
从 而 A F =
槡 2 A G = 2
槡 3 ,
故 P F = A F = 2
槡 3 . … … … … … … … … … … … … … … … … … … … … … … … … … … 1 0 分
1
2 2 ? ( 1 ) ; p = - x + 5 0 … … … … … … … … … … … … … … … … … … … … … … … … … … … 4 分
2
( 2 ) 从 第 2 1 天 到 第 4 0 天 中 , q 是 基 础 价 与 浮 动 价 的 和 , 其 中 基 础 价 保 持 不 变 , 浮 动 价 与 x
成 反 比 , b
m + = 4 5 ,
b 2 1
设 q = m + , 将 ( 2 1 , 4 5 ) 和 ( 3 5 , 3 5 ) 分 别 代 入 得
x b
m + = 3 5 .
{
3 5
m = 2 0 ,
解 得 { b = 5 2 5 .
5 2 5
所 以 q = 2 0 + . … … … … … … … … … … … … … … … … … … … … … … … … … … 8 分
x
( 3 ) 设 利 润 为 W , 1 1 2
前 2 0 天 , 即 1 ≤ x ≤ 2 0 时 , W = 3 0 + x - 2 0 ( - x + 5 0 ) = - ( x - 1 5 ) + 6 1 2 ? 5 ,
( 2 ) 2
∴ 当 x = 1 5 时 , W 有 最 大 值 , 最 大 值 为 6 1 2 ? 5 ?
第 2 1 天 到 第 4 0 天 , 即 2 1 ≤ x ≤ 4 0 时 ,
5 2 5 2 6 2 5 0
W = 2 0 + - 2 0 ( - x + 5 0 ) = - 5 2 5 ,
( x ) x
∵ W 随 x 的 增 大 而 减 小 , ∴ 当 x = 2 1 时 , W 有 最 大 值 , 最 大 值 为 7 2 5 元 ,
综 上 所 述 , 这 4 0 天 里 该 网 店 第 2 1 天 获 得 的 利 润 最 大 , 为 7 2 5 元 ? … … … … … 1 2 分
2 3 ? ( 1 ) 在 R t △ A B C 中 , A B = 6 , B C = 8 ,
2 2 2 2
∴ A C = 槡 A B + B C = 槡 6 + 8 = 1 0 ,
设 A P = x , C P = 1 0 - x ,
∵ A D ∥ B C ,
蚌 埠 市 九 年 级 数 学 参 考 答 案 第 3 页 ( 共 4 页 )
∴ R t △ A E P ∽ R t △ C F P ,
A E A P x 5 - 1
∴ = , 即 = 槡 , 解 得 : x = 1 5 - 5 5 ,
F C P C 1 0 - x 2 槡
∴ A P = 1 5 - 5
槡 5 . … … … … … … … … … … … … … … … … … … … … … … … … … … … 4 分
( 2 ) ① ∵ P M ⊥ P D , ∴ ∠ F P M + ∠ E P D = 9 0 ° ,
又 ∠ E D P + ∠ E P D = 9 0 ° ,
∴ ∠ F P M = ∠ E D P
∴ R t △ F P M ∽ R t △ E D P … … … … … … … … … … … … … … … … … … … … … … … 7 分
P M P F P F A B 3
∴ = = = = . … … … … … … … … … … … … … … … … … … … … 1 0 分
P D D E F C B C 4
② 当 P D ⊥ A C 时 , P D 最 短 , 矩 形 P M N D 面 积 最 小 ,
A D · D C 2 4
此 时 , P D = = ,
A C 5
3 1 8
P M = P D = ,
4 5
2 4 1 8 4 3 2
∴ S
矩 形 P M N D 最 小 值 为 × = . … … … … … … … … … … … … … … … … … … 1 4 分
5 5 2 5
( 其 它 解 法 请 根 据 以 上 评 分 标 准 酌 情 赋 分 )
蚌 埠 市 九 年 级 数 学 参 考 答 案 第 4 页 ( 共 4 页 )
九 年 级 数 学 ( 沪 科 版 )
考 试 时 间 : 1 2 0 分 钟 满 分 : 1 5 0 分
一 、 选 择 题 : ( 本 大 题 共 1 0 小 题 , 每 小 题 4 分 , 共 4 0 分 , 在 每 小 题 给 出 的 A , B , C , D 四 个 选 项 中 , 只 有
一 项 是 符 合 题 目 要 求 的 , 请 在 答 题 卷 上 将 正 确 答 案 的 字 母 代 号 涂 黑 )
2
1 ? 将 抛 物 线 y = 2 x + 1 向 右 平 移 2 个 单 位 , 再 向 下 平 移 3 个 单 位 , 则 平 移 后 的 抛 物 线 解 析 式 为
2 2
A ? y = 2 x + 3 B ? y = 2 ( x - 2 ) - 2
2 2
C ? y = 2 ( x + 2 ) - 2 D ? y = 2 ( x + 2 ) + 4
2 ? 在 直 角 坐 标 平 面 内 有 一 点 P ( 3 , 4 ) , O P 与 x 轴 正 半 轴 的 夹 角 为 α , 则 s in α 的 值 是
3 4 3 4
A ? B ? C ? D ?
4 3 5 5
3 ? 如 图 , 已 知 ∠ 1 = ∠ 2 , 则 添 加 下 列 一 个 条 件 后 , 仍 无 法 判 定 △ A B C ∽ △ A D E 的 是
A B B C A B A C
A ? = B ? = C ? ∠ B = ∠ A D E D ? ∠ C = ∠ E
A D D E A D A E
第 3 题 图 第 5 题 图 第 6 题 图
2
4 ? 已 知 点 A ( - 3 , y 1 ) , B ( 1 , y 2 ) 在 二 次 函 数 y = - ( x + 2 ) + m 的 图 象 上 , 则 y 1 , y 2 的 大 小 关
系 是
A ? y 1 < y 2 B ? y 1 > y 2 C ? y 1 = y 2 D ? 不 能 确 定
5 ? 如 图 , 四 边 形 A B C D 内 接 于 ⊙ O , 已 知 ∠ A D C = 1 4 0 ° , 则 ∠ A O C 的 大 小 是
A ? 8 0 ° B ? 7 0 ° C ? 6 0 ° D ? 4 0 °
S △ A B E
6 ? 如 图 , 将 一 副 三 角 尺 如 图 所 示 叠 放 在 一 起 , 其 中 ∠ B A C = ∠ A C D = 9 0 ° , 则 的 值 是
S △ D C E
1 1
A ? 3 B ? C ? 2 D ?
3 4
蚌 埠 市 九 年 级 数 学 试 卷 第 1 页 ( 共 6 页 )
书书书
7 ? 如 图 , 过 ⊙ O 外 一 点 P 作 圆 的 两 条 切 线 P A , P B , 切 点 分 别 为 A , B , 连 接 P O 并 延 长 交 ⊙ O 于
点 D , P D 交 A B 于 点 C . 下 列 结 论 不 一 定 成 立 的 是
獉 獉 獉
A ? △ B P A 为 等 腰 三 角 形 B ? P C 为 △ B P A 的 边 A B 上 的 中 线
C ? A B 与 P D 相 互 垂 直 平 分 D ? 点 A , B 都 在 以 P O 为 直 径 的 圆 上
3
8 ? 对 于 反 比 例 函 数 y = , 下 列 说 法 正 确 的 是
2 x
A ? 它 的 图 象 在 第 二 、 四 象 限
B ? 它 的 函 数 值 y 随 x 的 增 大 而 减 小
3
C ? 点 P 为 图 象 上 的 任 意 一 点 , 过 点 P 作 P A ⊥ x 轴 于 点 A , △ P O A 的 面 积 是 2
D ? 若 点 A ( - 1 , y 1 ) 和 点 B ( -
槡 3 , y 2 ) 在 这 个 函 数 图 象 上 , 则 y 1 < y 2
第 7 题 图 第 9 题 图 第 1 0 题 图
9 ? 《 九 章 算 术 》 是 我 国 古 代 著 名 数 学 著 作 , 书 中 记 载 : “ 今 有 圆 材 , 埋 在 壁 中 , 不 知 大 小 以 锯 锯
之 , 深 一 寸 , 锯 道 长 一 尺 , 问 径 几 何 ? ” 其 大 意 为 : “ 如 图 , C D 为 ⊙ O 的 直 径 , 弦 A B ⊥ D C 于
点 E , E D = 1 寸 , A B = 1 0 寸 , 求 直 径 C D 的 长 ? ” 则 C D 的 长 是
A ? 1 3 寸 B ? 2 0 寸 C ? 2 6 寸 D ? 2 8 寸
3
1 0 ? 如 图 , 矩 形 A B C D 中 , E 是 A B 的 中 点 , 将 △ A D E 沿 D E 翻 折 , 点 A 落 在 点 F 处 , s in ∠ A D E = ?
5
设 A B = x , △ A B F 的 面 积 为 y , 则 y 与 x 的 函 数 图 象 大 致 为
A ? B ? C ? D ?
蚌 埠 市 九 年 级 数 学 试 卷 第 2 页 ( 共 6 页 )
二 、 填 空 题 : ( 本 大 题 共 4 个 小 题 , 每 小 题 5 分 , 共 2 0 分 , 请 将 答 案 直 接 填 在 题 中 的 横 线 上 )
2
1 1 ? 抛 物 线 y = 2 x - 4 x + 4 的 顶 点 坐 标 为 ?
)
1 2 ? 如 图 , 在 6 × 6 的 正 方 形 网 格 中 , ⊙ O 经 过 格 点 A , B , C , 点 P 是 A C B 上 任 意 一 点 , 连 接 A P ,
B P , 则 ta n ∠ A P B 的 值 为 ?
1 3 ? 如 图 , 一 块 含 有 3 0 ° 角 的 直 角 三 角 板 A B C , 在 水 平 桌 面 上 绕 点 C 按 顺 时 针 方 向 旋 转 到 三 角
板 A ′ B ′ C ′ 的 位 置 , 若 A C = 3 c m , 则 顶 点 A 在 旋 转 过 程 中 所 经 过 的 路 径 长 为 c m ?
1 4 ? 如 图 , 在 R t △ A B C 中 , ∠ A C B = 9 0 ° , A C = 4 , B C = 6 , 点 D 是 边 B C 的 中 点 , 点 E 是 边 A B 上 的
任 意 一 点 ( 点 E 不 与 点 B 重 合 ) , 沿 D E 翻 折 △ D B E , 使 点 B 落 在 △ A B C 所 在 平 面 内 点 F
处 , 连 接 A F ?
( 1 ) 当 D E ⊥ B D 时 , D E 的 长 度 为 ;
( 2 ) 当 线 段 A F 的 长 取 最 小 值 时 , ta n ∠ F B D 的 值 为 ?
第 1 2 题 图 第 1 3 题 图 第 1 4 题 图
三 、 ( 本 题 共 两 小 题 , 每 小 题 8 分 , 共 1 6 分 )
2
1 5 ? 计 算 : s in 4 5 ° + c o s 3 0 ° · ta n 6 0 ° .
a + 4 b + 3 c + 8
1 6 ? 已 知 a , b , c 是 △ A B C 的 三 边 , 满 足 = = , 且 a + b + c = 1 2 .
3 2 4
( 1 ) 求 a , b , c 的 值 ;
( 2 ) 若 线 段 x 是 线 段 a , b 的 比 例 中 项 , 求 x ?
蚌 埠 市 九 年 级 数 学 试 卷 第 3 页 ( 共 6 页 )
四 、 ( 本 题 共 两 小 题 , 每 小 题 8 分 , 共 1 6 分 )
1 7 ? 如 图 , 在 平 面 直 角 坐 标 系 中 , 点 A , B 的 坐 标 分 别 为 ( 1 , 3 ) , ( 3 , 2 ) ?
第 1 7 题 图
( 1 ) 画 出 △ O A B 绕 点 B 顺 时 针 旋 转 9 0 ° 后 的 △ O ′ A ′ B ;
( 2 ) 以 点 B 为 位 似 中 心 , 相 似 比 为 2 ∶1 , 在 x 轴 的 上 方 画 出 △ O ′ A ′ B 放 大 后 的 △ O ″ A ″ B ;
( 3 ) 点 M 是 O A 的 中 点 , 在 ( 1 ) 和 ( 2 ) 的 变 换 下 , M 的 对 应 点 M ″ 的 坐 标 为 .
1 8 ? 为 进 一 步 加 强 疫 情 防 控 工 作 , 某 学 校 决 定 安 装 红 外 线 体 温 监 测 仪 , 该 设 备 通 过 探 测 人 体 红
外 辐 射 能 量 对 进 入 测 温 区 域 的 人 员 进 行 快 速 测 温 , 无 需 人 员 停 留 和 接 触 , 安 装 示 意 图 如
下 . 已 知 检 测 仪 探 测 线 与 地 面 A C 形 成 的 最 大 角 ∠ O B C = 7 5 ° , 最 小 角 ∠ O A C = 3 0 ° , 本 设 备
需 安 装 在 垂 直 于 水 平 地 面 A C 的 支 架 C P 上 ? 现 学 校 要 求 测 温 区 域 的 宽 度 A B 为 4 m , 请 你
帮 助 学 校 确 定 该 设 备 的 安 装 高 度 O C . ( 结 果 保 留 根 号 )
第 1 8 题 图
蚌 埠 市 九 年 级 数 学 试 卷 第 4 页 ( 共 6 页 )
五 、 ( 本 题 共 两 小 题 , 每 小 题 1 0 分 , 共 2 0 分 ) k
1 9 ? 如 图 , 在 平 面 直 角 坐 标 系 中 , 正 比 例 函 数 y = 3 x 与 反 比 例 函 数 y = ( k > 0 ) 的 图 象 交 于 A ,
x
B 两 点 , 点 A 的 横 坐 标 为 2 , A C ⊥ x 轴 , 垂 足 为 C , 连 接 B C .
( 1 ) 反 比 例 函 数 的 表 达 式 为 ; k
( 2 ) 正 比 例 函 数 y = 3 x 的 值 大 于 反 比 例 函 数 y = 的 值 时 x 的
x
取 值 范 围 是 ;
( 3 ) 求 △ A B C 的 面 积 .
第 1 9 题 图
2 0 ? 如 图 , B 为 ⊙ O 上 一 点 , A 为 ⊙ O 外 一 点 , 连 接 A B , A O , 线 段 A O 交 ⊙ O 于 点 C , A O 的 延 长 线
) 1
交 ⊙ O 于 点 D , E 是 B C D 上 不 与 B , D 重 合 的 点 , s in A = , ∠ B E D = 6 0 ° .
2
( 1 ) 求 证 : A B 是 ⊙ O 的 切 线 ;
( 2 ) 过 D 点 作 ⊙ O 的 切 线 D F , 交 A B 延 长 线 于 点 F , 若
D F = 3
槡 3 , 求 ⊙ O 的 半 径 ?
第 2 0 题 图
六 、 ( 本 题 满 分 1 2 分 )
2 1 ? 如 图 1 , 在 △ A B C 中 , A B = 4
槡 2 , ∠ B = 4 5 ° , ∠ C = 6 0 ° ?
( 1 ) 求 B C 边 上 的 高 线 长 ;
( 2 ) 如 图 2 , 若 点 E 为 线 段 A B 的 中 点 , 点 F 在 边 A C 上 , 连 接 E F , 沿 E F 将 △ A E F 折 叠 得 到
△ P E F ? 连 接 A P , 当 P F ⊥ A C 时 , 求 P F 的 长 ?
第 2 1 题 图
蚌 埠 市 九 年 级 数 学 试 卷 第 5 页 ( 共 6 页 )
七 、 ( 本 题 满 分 1 2 分 )
2 2 ? 某 大 学 生 利 用 暑 假 4 0 天 社 会 实 践 参 与 了 一 家 网 店 经 营 , 了 解 到 一 种 新 型 商 品 成 本 为 2 0
元 / 件 , 第 x 天 销 售 量 为 p 件 , 销 售 单 价 为 q 元 ? 经 跟 踪 调 查 发 现 , 这 4 0 天 中 p - 5 0 与 x 成
正 比 , 前 2 0 天 ( 包 含 第 2 0 天 ) , q 与 x 的 关 系 满 足 关 系 式 q = 3 0 + a x ; 从 第 2 1 天 到 第 4 0 天
中 , q 是 基 础 价 与 浮 动 价 的 和 , 其 中 基 础 价 保 持 不 变 , 浮 动 价 与 x 成 反 比 , 且 得 到 了 表 中 的
数 据 :
x ( 天 ) 1 0 2 1 3 5
q ( 元 / 件 ) 3 5 4 5 3 5
p ( 件 ) 4 0
( 1 ) 请 直 接 写 出 a 的 值 为 , 直 接 写 出 这 4 0 天 中 p 与 x 的 关 系 式 为 ;
( 2 ) 从 第 2 1 天 到 第 4 0 天 中 , 求 q 与 x 满 足 的 关 系 式 ;
( 3 ) 求 这 4 0 天 里 该 网 店 第 几 天 获 得 的 利 润 最 大 ? 最 大 为 多 少 ?
八 、 ( 本 题 满 分 1 4 分 )
2 3 ? 矩 形 A B C D 中 , A B = 6 , A D = 8 , 点 P 是 对 角 线 A C 上 一 动 点 ( 不 与 A , C 重 合 ) , 过 点 P 作 E F
⊥ B C , 分 别 交 A D , B C 于 点 E , F ?
( 1 ) 如 图 1 , 若 E 为 A D 的 黄 金 分 割 点 ( A E < D E ) , 求 A P 的 长 ;
( 2 ) 如 图 2 , 连 结 P D , 作 P M ⊥ P D , 交 射 线 B C 于 点 M , 以 线 段 P D , P M 为 邻 边 作 矩 形
P M N D .
P M
① 求 的 值 ;
P D
② 求 矩 形 P M N D 的 面 积 最 小 值 .
第 2 3 题 图
蚌 埠 市 九 年 级 数 学 试 卷 第 6 页 ( 共 6 页 )
蚌 埠 市 2 0 2 0 — 2 0 2 1 学 年 度 第 一 学 期 期 末 教 学 质 量 监 测
九 年 级 数 学 ( 沪 科 版 ) 参 考 答 案 及 评 分 标 准
一 、 选 择 题
题 号 1 2 3 4 5 6 7 8 9 1 0
答 案 B D A B A B C D C C
二 、 填 空 题 1 1
1 1 ? ( 1 , 2 ) 1 2 ? 1 3 ? 2 π 1 4 ? ( 1 ) 2 ( 2 )
2 2
三 、 解 答 题
2 2 3 1 3
1 5 ? 解 : 原 式 = ( 槡 ) + 槡 × 3 = + = 2 ? … … … … … … … … … … … … … … … … … … 8 分
2 2 槡 2 2
a + 4 b + 3 c + 8
1 6 ? ( 1 ) ∵ = = , 且 a + b + c = 1 2 ,
3 2 4
a + 4 b + 3 c + 8 a + 4 + b + 3 + c + 8 a + b + c + 1 5 1 2 + 1 5
∴ = = = = = = 3 ,
3 2 4 3 + 2 + 4 9 9
a + 4 b + 3 c + 8
∴ = 3 , = 3 , = 3 ,
3 2 4
∴ a = 5 , b = 3 , c = 4 ; … … … … … … … … … … … … … … … … … … … … … … … … … … 4 分
( 2 ) ∵ 线 段 x 是 线 段 a 、 b 的 比 例 中 项 ,
2
∴ x = 3 × 5 = 1 5 ,
∴ x =
槡 1 5 ( x = -
槡 1 5 舍 去 ) . … … … … … … … … … … … … … … … … … … … … … 8 分
1 7 ? ( 1 ) 如 图 , △ O ′ A ′ B 即 为 所 求 ; … … … … … … … … … … … … … … … … … … … … … … … 3 分
( 2 ) 如 图 , △ O ″ A ″ B 即 为 所 求 ; … … … … … … … … … … … … … … … … … … … … … … … 6 分
( 3 ) ( 2 , 7 ) ? … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … 8 分
蚌 埠 市 九 年 级 数 学 参 考 答 案 第 1 页 ( 共 4 页 )
1 8 ? 解 : 根 据 题 意 可 知 : O C ⊥ A C , ∠ O B C = 7 5 ° , ∠ O A C = 3 0 ° , A B = 4 m ,
过 B 点 作 B D ⊥ O A , 垂 足 为 D , 则 ∠ D B O = ∠ D O B = 4 5 ° , … … … … … … … … … … … … 2 分
且 在 R t △ A B D 中 , B D = 2 , A D = 2
槡 3 , … … … … … … … … … … … … … … … … … … … … 4 分
在 R t △ O B D 中 , O D = B D = 2 ,
∴ O A = A D + O D = 2
槡 3 + 2 , … … … … … … … … … … … … … … … … … … … … … … … … 6 分
1
在 R t △ O A C 中 , O C = O A = 3 + 1 ,
2 槡
答 : 该 设 备 的 安 装 高 度 O C 为 ( 槡 3 + 1 ) m ? … … … … … … … … … … … … … … … … … … 8 分
1 2
1 9 ? ( 1 ) y = ; … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … … 3 分
x
( 2 ) - 2 < x < 0 或 x > 2 ; … … … … … … … … … … … … … … … … … … … … … … … … … 6 分
( 3 ) ∵ A 点 横 坐 标 2 , y = 2 × 3 = 6 .
∴ A 点 坐 标 为 ( 2 , 6 )
∵ A , B 关 于 原 点 对 称 ,
∴ B 点 坐 标 为 ( - 2 , - 6 ) ,
∴ B 到 O C 的 距 离 为 6 , 1
∴ S △ A B C = S △ A O C + S △ B O C = 2 S △ A O C = × 2 × 6 × 2 = 1 2 . … … … … … … … … … … … 1 0 分
2
2 0 ? ( 1 ) 证 明 : 连 接 O B , 如 图 1 ,
∵ ∠ B E D = 6 0 °
∴ ∠ B O D = 2 ∠ B E D = 1 2 0 ° ;
∴ ∠ A O B = 6 0 ° ,
1
∵ s in A = ,
2 图 1
∴ ∠ A = 3 0 ° ,
∴ ∠ A B O = 9 0 ° , 即 A B ⊥ O B ,
∴ A B 是 ⊙ O 的 切 线 ; … … … … … … … … … … … … … … … … … … … … … … … … … 5 分
( 2 ) 解 : 连 接 O F , O B , 如 图 2 ,
∵ D F , A B 是 ⊙ O 的 切 线 ,
∴ ∠ O D F = ∠ O B F = 9 0 ° ,
∵ O F = O F , O B = O D ,
∴ △ B O F ≌ △ D O F ( H L ) , 图 2
∴ ∠ B O F = ∠ D O F = 6 0 ° ,
在 R t △ D O F 中 , ∠ D O F = 6 0 ° , D F = 3
槡 3 ,
D F 3 3
∴ O D = = 槡 = 3 ,
ta n ∠ D O F
槡 3
蚌 埠 市 九 年 级 数 学 参 考 答 案 第 2 页 ( 共 4 页 )
∴ ⊙ O 的 半 径 为 3 ? … … … … … … … … … … … … … … … … … … … … … … … … … 1 0 分
2 1 ? ( 1 ) 作 A D ⊥ B C 于 D .
2
在 R t △ A B D 中 , A D = A B · s in 4 5 ° = 4
槡 2 × 槡 = 4 . … … … … … … … … … … … … … 4 分
2
( 2 ) 由 题 意 , ∠ B A C = 7 5 ° ,
又 P F ⊥ A C 时 , ∠ A F E = 4 5 ° ,
∴ ∠ A E F = 6 0 ° . … … … … … … … … … … … … … … … … … … … … … … … … … … … 6 分
易 知 A E = 2
槡 2 ,
设 A P 交 E F 于 点 G , 则 ∠ A G E = 9 0 ° ,
∴ E G =
槡 2 , A G =
槡 6 … … … … … … … … … … … … … … … … … … … … … … … … … … 8 分
从 而 A F =
槡 2 A G = 2
槡 3 ,
故 P F = A F = 2
槡 3 . … … … … … … … … … … … … … … … … … … … … … … … … … … 1 0 分
1
2 2 ? ( 1 ) ; p = - x + 5 0 … … … … … … … … … … … … … … … … … … … … … … … … … … … 4 分
2
( 2 ) 从 第 2 1 天 到 第 4 0 天 中 , q 是 基 础 价 与 浮 动 价 的 和 , 其 中 基 础 价 保 持 不 变 , 浮 动 价 与 x
成 反 比 , b
m + = 4 5 ,
b 2 1
设 q = m + , 将 ( 2 1 , 4 5 ) 和 ( 3 5 , 3 5 ) 分 别 代 入 得
x b
m + = 3 5 .
{
3 5
m = 2 0 ,
解 得 { b = 5 2 5 .
5 2 5
所 以 q = 2 0 + . … … … … … … … … … … … … … … … … … … … … … … … … … … 8 分
x
( 3 ) 设 利 润 为 W , 1 1 2
前 2 0 天 , 即 1 ≤ x ≤ 2 0 时 , W = 3 0 + x - 2 0 ( - x + 5 0 ) = - ( x - 1 5 ) + 6 1 2 ? 5 ,
( 2 ) 2
∴ 当 x = 1 5 时 , W 有 最 大 值 , 最 大 值 为 6 1 2 ? 5 ?
第 2 1 天 到 第 4 0 天 , 即 2 1 ≤ x ≤ 4 0 时 ,
5 2 5 2 6 2 5 0
W = 2 0 + - 2 0 ( - x + 5 0 ) = - 5 2 5 ,
( x ) x
∵ W 随 x 的 增 大 而 减 小 , ∴ 当 x = 2 1 时 , W 有 最 大 值 , 最 大 值 为 7 2 5 元 ,
综 上 所 述 , 这 4 0 天 里 该 网 店 第 2 1 天 获 得 的 利 润 最 大 , 为 7 2 5 元 ? … … … … … 1 2 分
2 3 ? ( 1 ) 在 R t △ A B C 中 , A B = 6 , B C = 8 ,
2 2 2 2
∴ A C = 槡 A B + B C = 槡 6 + 8 = 1 0 ,
设 A P = x , C P = 1 0 - x ,
∵ A D ∥ B C ,
蚌 埠 市 九 年 级 数 学 参 考 答 案 第 3 页 ( 共 4 页 )
∴ R t △ A E P ∽ R t △ C F P ,
A E A P x 5 - 1
∴ = , 即 = 槡 , 解 得 : x = 1 5 - 5 5 ,
F C P C 1 0 - x 2 槡
∴ A P = 1 5 - 5
槡 5 . … … … … … … … … … … … … … … … … … … … … … … … … … … … 4 分
( 2 ) ① ∵ P M ⊥ P D , ∴ ∠ F P M + ∠ E P D = 9 0 ° ,
又 ∠ E D P + ∠ E P D = 9 0 ° ,
∴ ∠ F P M = ∠ E D P
∴ R t △ F P M ∽ R t △ E D P … … … … … … … … … … … … … … … … … … … … … … … 7 分
P M P F P F A B 3
∴ = = = = . … … … … … … … … … … … … … … … … … … … … 1 0 分
P D D E F C B C 4
② 当 P D ⊥ A C 时 , P D 最 短 , 矩 形 P M N D 面 积 最 小 ,
A D · D C 2 4
此 时 , P D = = ,
A C 5
3 1 8
P M = P D = ,
4 5
2 4 1 8 4 3 2
∴ S
矩 形 P M N D 最 小 值 为 × = . … … … … … … … … … … … … … … … … … … 1 4 分
5 5 2 5
( 其 它 解 法 请 根 据 以 上 评 分 标 准 酌 情 赋 分 )
蚌 埠 市 九 年 级 数 学 参 考 答 案 第 4 页 ( 共 4 页 )
同课章节目录
