上海市 金山区2020-2021学年第一学期期末质量检测九年级数学(一模)试卷(PDF版含答案)
文档属性
| 名称 | 上海市 金山区2020-2021学年第一学期期末质量检测九年级数学(一模)试卷(PDF版含答案) |  | |
| 格式 | |||
| 文件大小 | 469.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 07:28:02 | ||
图片预览



文档简介
金山区 2020 学年第一学期期末质量检测
初三 数学试卷
(满分 150分,考试时间 100分钟)( 2021. 1)
一、选择题:( 本大题共 6题,每题 4分,满分 24分 )
【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸
的相应位置上.】
1.已知二次函数 ,那么该二次函数图像的对称轴是( )
( A)直线 ; ( B)直 线 ; ( C)直线 ; ( D)直线 .
2.下列各点在抛物线 上的是( )
( A) ; ( B) ; ( C) ; ( D) .
3.在 中, ,那么锐角 的正弦等于( )
( A) ;( B) ;( C) ;( D) .
4.若 是锐角, ,那么锐角 等于( )
( A) ; ( B) ; ( C) ; ( D) .
5.如图,已知点 、 分别在 的边 、 上, , , ,
,那么 等于( )
( A) ; ( B) ; ( C) ; ( D) .
6.如图,已知 中, , , ,如果以点 为圆心的圆与斜
边 有公共点,那么 ⊙ 的半径 的取值范围是 ( )
( A) ; ( B) ; ( C) ; ( D) .
A B
D E
B C
第 5题图 C A
第 6题图
二、 填空 题 :( 本大题共 12题,每题 4分,满分 48分)
【请直接将结果填入答题纸的相应位置】
1
7.计算: .
8.已知 ,那么 .
9.抛物线 沿着 轴正方向看,在 轴的左侧部分是 .(填“上升”或“下降”)
10.正十边形的中心角等于 度.
11.已知 ⊙ 和⊙ 的半径长分别为 和 ,若⊙ 和⊙ 内切,那么圆心距 的长
等于 .
12.在 中, , , ,那么 .
13.在 中, ,那么 .
14.已知: 如图, 的中线 与 交于点 , 交 于 ,那么
.
15.如图,在梯形 中, , ,设 , ,那么向量
用向量 、 表示为 .
16.如图,已知 ⊙ 中, ,弦 ,那么⊙ 的半径长等于 .
A
A D
D O
G
A B
B F C
E
C
第 14题图 B 第 15题图 第 16题图
17.如图,在 □ 中,点 在边 上, 交对角线 于 ,若 ,
的面积等于 ,那么 的面积等于 .
18.已知在 中, , , ,以点 为直角顶点的 的
顶点 在 的延长线上, 交 的延长线于点 ,若 , ,
A
那么 的长等于 .
E
B C
F
A D
第 17题图 B C
第 18题图
2
三、 解答题( 本大题 共 7题 ,满分 78分 )
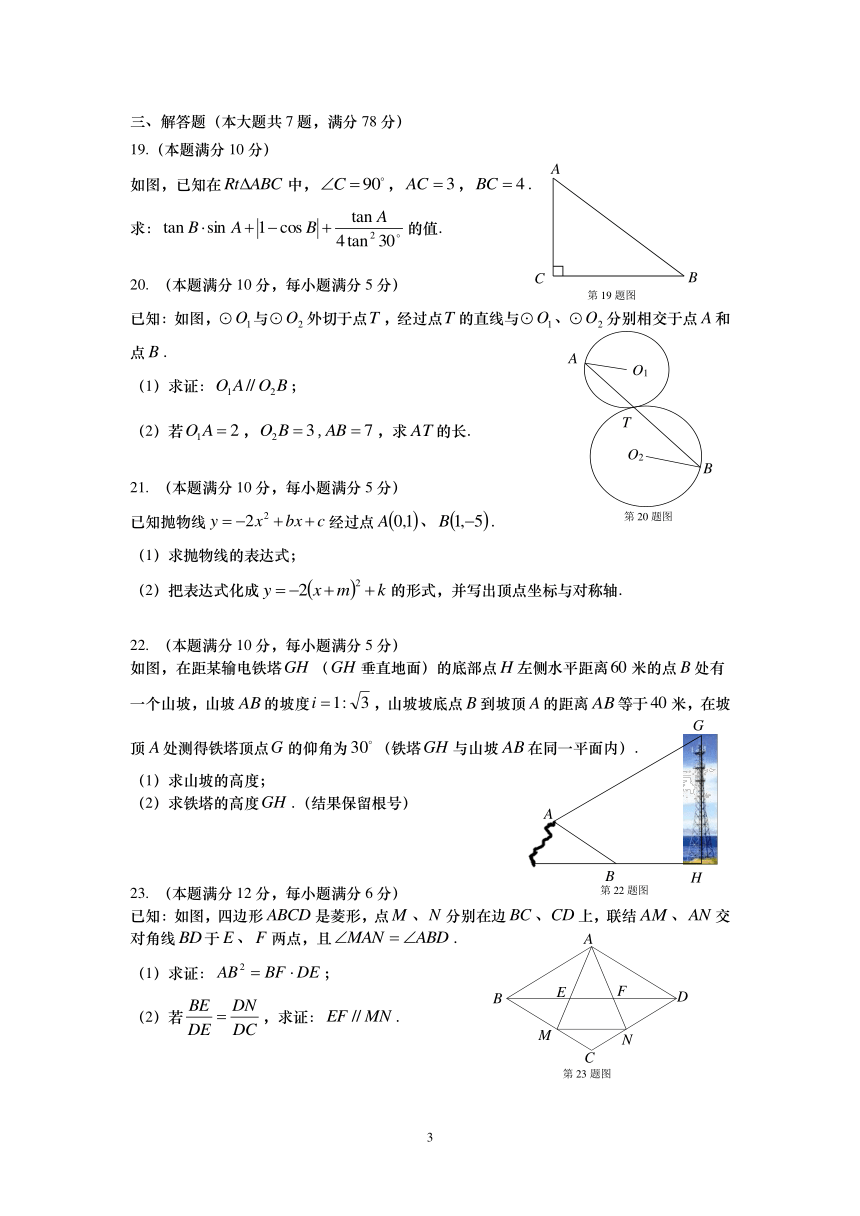
19.( 本题满分 10分 )
A
如 图,已知在 中, , , .
求: 的值 .
20. ( 本题 满分 10分,每 小题 满分 5分 ) C B
第 19题图
已知:如图, ⊙ 与⊙ 外切于点 ,经过点 的直线与⊙ 、⊙ 分别相交于点 和
点 . A
O1
( 1) 求证: ;
T
( 2) 若 , , ,求 的长 .
O2
B
21. ( 本题 满 分 10分,每 小题 满分 5分)
第 题图
已知抛物线 经过点 、 . 20
( 1) 求抛物线的表达式;
( 2) 把表达式化成 的形式,并写出顶点坐标与对称轴 .
22. ( 本题 满分 10分,每 小题 满分 5分 )
如图,在距某输电铁塔 ( 垂直地面)的底部点 左侧水平距离 米的点 处有
一个山坡,山坡 的坡度 ,山坡坡底点 到坡顶 的距离 等于 米,在坡
G
顶 处测得铁塔顶点 的仰角为 (铁塔 与山坡 在同一平面内) .
( 1)求山坡的 高度;
( 2) 求铁塔的高度 .(结果保留根号)
A
B H
23. ( 本题 满分 12分,每 小题 满分 6分 ) 第 22题图
已知:如图,四边形 是菱形,点 、 分别在边 、 上,联结 、 交
对角线 于 、 两点,且 . A
( 1) 求证: ;
F
B E D
( 2) 若 ,求证: .
M N
C
第 23题图
3
24. ( 本题满分 12分,每小题满分 4分 )
在平面直角坐标系 中,直线 与直线 相交于点 ,抛物线
经过点 .
( 1)求点 的坐标;
( 2) 若抛物线 向上平移两个单位后,
经过点 ,求抛物线 的表达式;
( 3) 若抛物线 与 关于 轴
对称,且这两条抛物线的顶点分别是点 与点 ,当 时,
求抛物线 的表达式 . 第 24题图
25. (本题 满分 14分,第 (1)分 4分, 第 (2)分 6分, 第 (3)分 4分 )
定理:一条弧所对的圆周角等于这条弧所对的圆心角的一半 .如图 1中, .
已知:如图 2, 是 ⊙ 的一条弦,点 在⊙ 上(与 、 不重合),联结 交射
线 于点 ,联结 ,⊙ 的半径为 , .
(1)求弦 的长 .
(2)当点 在线段 上时, 若 与 相似,求 的正切值 .
(3)当 时,求点 与 点 之间的距离(直接写出答案) .
A
O O
O
D E
A C
B A C
C
第 25题图 1
第 25题图 2 第 25题备用图
4
参 考 答 案 和 评 分 标 准
一.选择题: 1. A; 2. C; 3. B; 4. B; 5. D; 6. C.
二.填空题: 7. ; 8. ; 9. 上升 ; 10. ; 11. ; 12. ; 13. ;
14. ; 15. ; 16. ; 17. ; 18. .
19.解: 在 中, , , ,由勾股定理得, ,
∴ ;……………………………………( 2分)
∴ ; ; ; ……( 4分)
∴原式 ;……………………( 2分)
.………………( 2分)
20.( 1)证明:联结 ,即 为连心线,又 ∵ ⊙ 与⊙ 外切于点 , ……( 1分)
∴ 经过点 ; ………………………………………( 1分)
∵ ; ∴ ; ……………………( 1分)
∵ ; ∴ ; ……………( 1分)
∴ .……………………( 1分)
( 2) ∵ ∴ ; ……………………………( 2分)
∵ , , ; ∴ ,解得: .……………( 3分)
21. 解: ( 1)由 抛物线 经过点 、 两点可得:
………………( 2分) 解得: ; …………………( 2分)
∴ 抛物线的解析式为: .……………………( 1分)
( 2) ; ……………( 3分)
5
∴ ,顶点坐标为: ,对称轴为:直线 .……………( 1+1分)
22. 解: ( 1)过点 作 垂直 ,交 的延长线于点 .……………( 1分)
即 ;
由题意得: , (米); ∴ ,即 ;………( 1分)
又∵ ,即 ……………( 1分)
∴ (米) .……………( 1分)
答: 山坡的高度为 米 .…………………( 1分)
( 2)作 交 于点 .………………( 1分)
∵ , ;∴ ;
即:四边形 是平行四边形;
由题意可知: , (米);
∵ (米); ∴ (米); ……………( 1分)
在 中, ; ∴ (米) .……………( 1分)
又∵ (米) ;
∴ (米) ;……………( 1分)
答: 铁塔的高度 为 米 .……………( 1分)
23. 证明:( 1) ∵ 四边形 是菱形 ;
∴ ; ……………( 1分)
∴ ; ……………( 1分)
∵ , ;
又 ∵ ;
∴ ; ……………( 1分)
∴ ∽ ; ……………( 1分)
∴ ,即 ; ……………( 1分)
∴ .……………( 1分)
6
( 2) ∵ 四边形 是菱形 ;
∴ , ; ……………( 1分)
∴ ;……………( 2分) ∵ ;
∴ , ……………( 1分)∴ ;……………( 1分)
∴ , 即 .……………( 1分)
24.解: ( 1) ∵ 直线 与直线 相交于点 ,
∴ ,解得: ;……………( 3分)
∴ 点 的坐标为 .……………( 1分)
( 2) ∵ 抛物线 经过点 ,
∴ 即 ……………( 1分)
∴
∴ 平移后的抛物线的表达式是 ; ……………( 1分)
∴ ,解得: ………………( 1分)
∴抛物线 的表达式是: .……………( 1分)
( 3) ∵
∴ ……………( 1分)
∵ 抛物线 与 关于 轴对称,
∴ ……………( 1分)
∵ , ∴ ;
∴ ;
又 ∵ , ;
7
∴ ,解得: .………( 1分)
∴抛物线 的表达式是 .………………( 1分)
25. ( 1) 解: 作 垂足为点 , 过圆心,
由垂径定理得: ; ……………………………( 1分)
∵ 在 中 ,设 , ……………( 1分)
∴ 在 中,可得: ,由 ⊙ 的半径为 可得: ,
解得: ,( 舍去) ∴ ,………………………( 1分)
∴ .………………………( 1分)
(2)∵ ,
∴当 与 相似时可得: 或者 ;
由定理: 一条弧所对的圆周角等于这条弧所对的圆心角的一半 .可知: ,
∴
∴当 与 相似时不存在 情况 .………………………( 1分)
∴当 与 相似时, ,
∴ ,∴ ;……………( 1分)
∵ ,得 ,∴ ;…………………( 1分)
作 垂足为 ,可 得: ,∴ ,
∴ 即 ,
∴ ,……………( 1分) O
D
E
, ,…………( 1分)
A G H C
∴在 中,
.…………………………( 1分)
( 3) 当 时, 的长是 或 .……………………………( 2+2分)
8
初三 数学试卷
(满分 150分,考试时间 100分钟)( 2021. 1)
一、选择题:( 本大题共 6题,每题 4分,满分 24分 )
【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸
的相应位置上.】
1.已知二次函数 ,那么该二次函数图像的对称轴是( )
( A)直线 ; ( B)直 线 ; ( C)直线 ; ( D)直线 .
2.下列各点在抛物线 上的是( )
( A) ; ( B) ; ( C) ; ( D) .
3.在 中, ,那么锐角 的正弦等于( )
( A) ;( B) ;( C) ;( D) .
4.若 是锐角, ,那么锐角 等于( )
( A) ; ( B) ; ( C) ; ( D) .
5.如图,已知点 、 分别在 的边 、 上, , , ,
,那么 等于( )
( A) ; ( B) ; ( C) ; ( D) .
6.如图,已知 中, , , ,如果以点 为圆心的圆与斜
边 有公共点,那么 ⊙ 的半径 的取值范围是 ( )
( A) ; ( B) ; ( C) ; ( D) .
A B
D E
B C
第 5题图 C A
第 6题图
二、 填空 题 :( 本大题共 12题,每题 4分,满分 48分)
【请直接将结果填入答题纸的相应位置】
1
7.计算: .
8.已知 ,那么 .
9.抛物线 沿着 轴正方向看,在 轴的左侧部分是 .(填“上升”或“下降”)
10.正十边形的中心角等于 度.
11.已知 ⊙ 和⊙ 的半径长分别为 和 ,若⊙ 和⊙ 内切,那么圆心距 的长
等于 .
12.在 中, , , ,那么 .
13.在 中, ,那么 .
14.已知: 如图, 的中线 与 交于点 , 交 于 ,那么
.
15.如图,在梯形 中, , ,设 , ,那么向量
用向量 、 表示为 .
16.如图,已知 ⊙ 中, ,弦 ,那么⊙ 的半径长等于 .
A
A D
D O
G
A B
B F C
E
C
第 14题图 B 第 15题图 第 16题图
17.如图,在 □ 中,点 在边 上, 交对角线 于 ,若 ,
的面积等于 ,那么 的面积等于 .
18.已知在 中, , , ,以点 为直角顶点的 的
顶点 在 的延长线上, 交 的延长线于点 ,若 , ,
A
那么 的长等于 .
E
B C
F
A D
第 17题图 B C
第 18题图
2
三、 解答题( 本大题 共 7题 ,满分 78分 )
19.( 本题满分 10分 )
A
如 图,已知在 中, , , .
求: 的值 .
20. ( 本题 满分 10分,每 小题 满分 5分 ) C B
第 19题图
已知:如图, ⊙ 与⊙ 外切于点 ,经过点 的直线与⊙ 、⊙ 分别相交于点 和
点 . A
O1
( 1) 求证: ;
T
( 2) 若 , , ,求 的长 .
O2
B
21. ( 本题 满 分 10分,每 小题 满分 5分)
第 题图
已知抛物线 经过点 、 . 20
( 1) 求抛物线的表达式;
( 2) 把表达式化成 的形式,并写出顶点坐标与对称轴 .
22. ( 本题 满分 10分,每 小题 满分 5分 )
如图,在距某输电铁塔 ( 垂直地面)的底部点 左侧水平距离 米的点 处有
一个山坡,山坡 的坡度 ,山坡坡底点 到坡顶 的距离 等于 米,在坡
G
顶 处测得铁塔顶点 的仰角为 (铁塔 与山坡 在同一平面内) .
( 1)求山坡的 高度;
( 2) 求铁塔的高度 .(结果保留根号)
A
B H
23. ( 本题 满分 12分,每 小题 满分 6分 ) 第 22题图
已知:如图,四边形 是菱形,点 、 分别在边 、 上,联结 、 交
对角线 于 、 两点,且 . A
( 1) 求证: ;
F
B E D
( 2) 若 ,求证: .
M N
C
第 23题图
3
24. ( 本题满分 12分,每小题满分 4分 )
在平面直角坐标系 中,直线 与直线 相交于点 ,抛物线
经过点 .
( 1)求点 的坐标;
( 2) 若抛物线 向上平移两个单位后,
经过点 ,求抛物线 的表达式;
( 3) 若抛物线 与 关于 轴
对称,且这两条抛物线的顶点分别是点 与点 ,当 时,
求抛物线 的表达式 . 第 24题图
25. (本题 满分 14分,第 (1)分 4分, 第 (2)分 6分, 第 (3)分 4分 )
定理:一条弧所对的圆周角等于这条弧所对的圆心角的一半 .如图 1中, .
已知:如图 2, 是 ⊙ 的一条弦,点 在⊙ 上(与 、 不重合),联结 交射
线 于点 ,联结 ,⊙ 的半径为 , .
(1)求弦 的长 .
(2)当点 在线段 上时, 若 与 相似,求 的正切值 .
(3)当 时,求点 与 点 之间的距离(直接写出答案) .
A
O O
O
D E
A C
B A C
C
第 25题图 1
第 25题图 2 第 25题备用图
4
参 考 答 案 和 评 分 标 准
一.选择题: 1. A; 2. C; 3. B; 4. B; 5. D; 6. C.
二.填空题: 7. ; 8. ; 9. 上升 ; 10. ; 11. ; 12. ; 13. ;
14. ; 15. ; 16. ; 17. ; 18. .
19.解: 在 中, , , ,由勾股定理得, ,
∴ ;……………………………………( 2分)
∴ ; ; ; ……( 4分)
∴原式 ;……………………( 2分)
.………………( 2分)
20.( 1)证明:联结 ,即 为连心线,又 ∵ ⊙ 与⊙ 外切于点 , ……( 1分)
∴ 经过点 ; ………………………………………( 1分)
∵ ; ∴ ; ……………………( 1分)
∵ ; ∴ ; ……………( 1分)
∴ .……………………( 1分)
( 2) ∵ ∴ ; ……………………………( 2分)
∵ , , ; ∴ ,解得: .……………( 3分)
21. 解: ( 1)由 抛物线 经过点 、 两点可得:
………………( 2分) 解得: ; …………………( 2分)
∴ 抛物线的解析式为: .……………………( 1分)
( 2) ; ……………( 3分)
5
∴ ,顶点坐标为: ,对称轴为:直线 .……………( 1+1分)
22. 解: ( 1)过点 作 垂直 ,交 的延长线于点 .……………( 1分)
即 ;
由题意得: , (米); ∴ ,即 ;………( 1分)
又∵ ,即 ……………( 1分)
∴ (米) .……………( 1分)
答: 山坡的高度为 米 .…………………( 1分)
( 2)作 交 于点 .………………( 1分)
∵ , ;∴ ;
即:四边形 是平行四边形;
由题意可知: , (米);
∵ (米); ∴ (米); ……………( 1分)
在 中, ; ∴ (米) .……………( 1分)
又∵ (米) ;
∴ (米) ;……………( 1分)
答: 铁塔的高度 为 米 .……………( 1分)
23. 证明:( 1) ∵ 四边形 是菱形 ;
∴ ; ……………( 1分)
∴ ; ……………( 1分)
∵ , ;
又 ∵ ;
∴ ; ……………( 1分)
∴ ∽ ; ……………( 1分)
∴ ,即 ; ……………( 1分)
∴ .……………( 1分)
6
( 2) ∵ 四边形 是菱形 ;
∴ , ; ……………( 1分)
∴ ;……………( 2分) ∵ ;
∴ , ……………( 1分)∴ ;……………( 1分)
∴ , 即 .……………( 1分)
24.解: ( 1) ∵ 直线 与直线 相交于点 ,
∴ ,解得: ;……………( 3分)
∴ 点 的坐标为 .……………( 1分)
( 2) ∵ 抛物线 经过点 ,
∴ 即 ……………( 1分)
∴
∴ 平移后的抛物线的表达式是 ; ……………( 1分)
∴ ,解得: ………………( 1分)
∴抛物线 的表达式是: .……………( 1分)
( 3) ∵
∴ ……………( 1分)
∵ 抛物线 与 关于 轴对称,
∴ ……………( 1分)
∵ , ∴ ;
∴ ;
又 ∵ , ;
7
∴ ,解得: .………( 1分)
∴抛物线 的表达式是 .………………( 1分)
25. ( 1) 解: 作 垂足为点 , 过圆心,
由垂径定理得: ; ……………………………( 1分)
∵ 在 中 ,设 , ……………( 1分)
∴ 在 中,可得: ,由 ⊙ 的半径为 可得: ,
解得: ,( 舍去) ∴ ,………………………( 1分)
∴ .………………………( 1分)
(2)∵ ,
∴当 与 相似时可得: 或者 ;
由定理: 一条弧所对的圆周角等于这条弧所对的圆心角的一半 .可知: ,
∴
∴当 与 相似时不存在 情况 .………………………( 1分)
∴当 与 相似时, ,
∴ ,∴ ;……………( 1分)
∵ ,得 ,∴ ;…………………( 1分)
作 垂足为 ,可 得: ,∴ ,
∴ 即 ,
∴ ,……………( 1分) O
D
E
, ,…………( 1分)
A G H C
∴在 中,
.…………………………( 1分)
( 3) 当 时, 的长是 或 .……………………………( 2+2分)
8
同课章节目录
