北师大版数学八年级下册3.4 简单的图案设计 课件(21张)
文档属性
| 名称 | 北师大版数学八年级下册3.4 简单的图案设计 课件(21张) |  | |
| 格式 | pptx | ||
| 文件大小 | 342.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 16:20:02 | ||
图片预览







文档简介
第三章 图形的平移与旋转
4 简单的图案设计
分析图案设计图案.(重点、难点)
学习目标
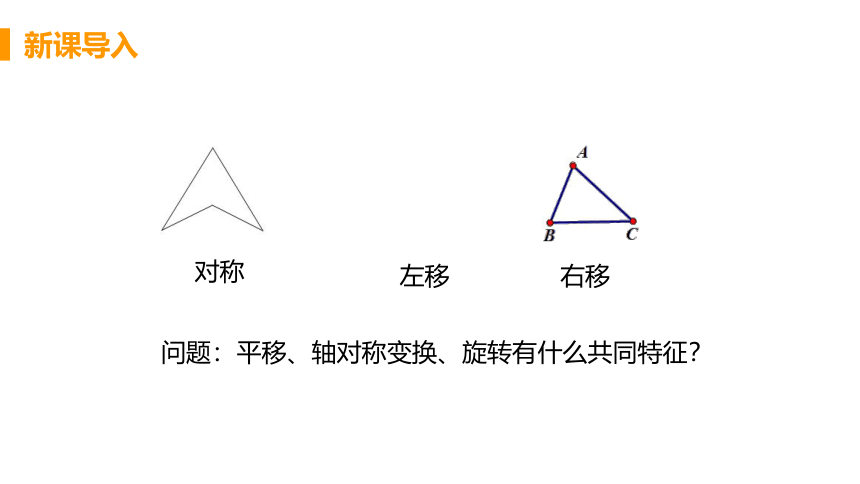
新课导入
问题:平移、轴对称变换、旋转有什么共同特征?
对称
左移
右移
新课讲解
知识点1 分析图案
观察下面的图案,分析它是将哪种基本图形经过了哪些变换后得到的?
将 经过旋转、
轴对称和平移得到的.
新课讲解
1.平面图案的形成依据:平移,旋转和轴对称.
2.图形的变换不改变图形的形状和大小,只改变
图形的位置.
新课讲解
3. 常见的变换类型有:
(1)平移变换;
(2)旋转变换;
(3)轴对称变换;
(4)旋转变换与平移变换的组合;
(5)旋转变换与轴对称变换的组合;
(6)轴对称变换与平移变换的组合.
新课讲解
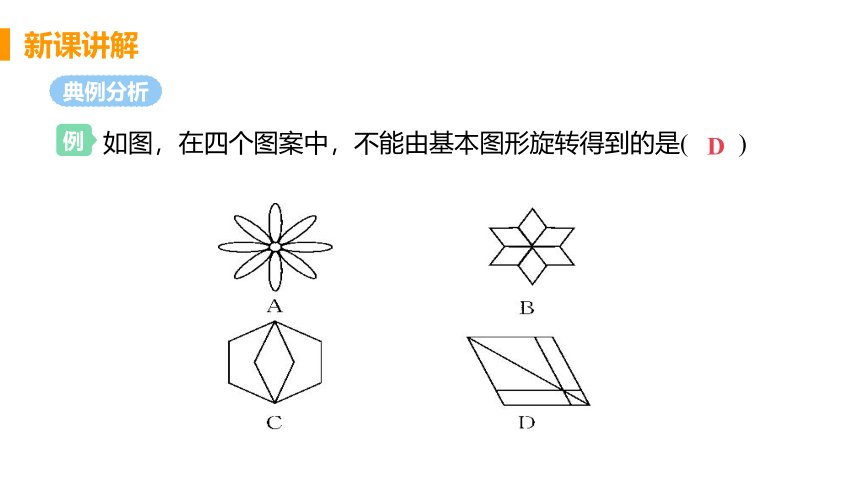
例
典例分析
如图,在四个图案中,不能由基本图形旋转得到的是( )
D
新课讲解
分析:
寻找基本图形、旋转中心、旋转角、旋转次数,
逐一判断.A.可由一个基本“花瓣”绕其中心
经过7次旋转,每次旋转45°得到;B.可由一个
基本“菱形”绕其中心经过5次旋转,每次旋转
60°得到;C.可由一个基本图形绕其中心旋转
180°得到;D.不能由基本图形旋转得到.
新课讲解
练一练
如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形既是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有( )
A.2种 B.3种
C.4种 D.5种
C
新课讲解
知识点2 设计图案
图案设计的一般步骤:
(1)选择基本图案(基本图案可以是一个图案,也可
以是几个图案的结合).
(2)对基本图案进行变换(变换可以是单纯的平移,
旋转或轴对称,也可以是多种变换).
(3)对图案进行修饰.
新课讲解
例
典例分析
学校在艺术周上,要求学生制作一个精美的轴对称图形,请你用所给出的几何图形:○○△△--(两个圆,两个等边三角形,两条线段)为构件,构思一个独特、有意义的轴对称图形,并写上一句简要的解说词.
分析:
解答本例需要利用给定的六个元素,充分展开想
象的翅膀,组合成各种有意义的图形.此外,还
要有一定的生活经验和一定的文学修养.
新课讲解
所设计图形如图所示(答案不唯一,可供参考):
解:
新课讲解
例
典例分析
把如图所示图形中左上角的图案绕着中心O旋
转90°,180°,270°,画出你所得的图案.
新课讲解
分析:
根据旋转图形的特征,分别把如上图 (1)(2)(3)所
示图形中左上角的图案绕着中心O旋转90°,
180°,270°,点O的位置不动,其余各部分均
绕点O按相同的方向旋转90°,180°,270°,
据此可画出各图.
新课讲解
画出的图案如图所示.
解:
课堂小结
图案设计的一般步骤:
(1)选择基本图案(基本图案可以是一个图案,也可
以是几个图案的结合).
(2)对基本图案进行变换(变换可以是单纯的平移,
旋转或轴对称,也可以是多种变换).
(3)对图案进行修饰.
当堂小练
1.国旗上的四个小五角星,通过怎样的移动可以相互得到( )
A.轴对称 B.平移 C.旋转 D.平移和旋转
2.起重机将重物垂直提起,这可以看作为数学上的( )
A.轴对称 B.平移 C.旋转 D.变形
D
B
当堂小练
3.下图是由12个全等三角形组成的,利用平移、轴对称或旋转分析这个图案的形成过程.
当堂小练
解:这个图形可以按照以下步骤形成的.
①以一个三角形的一条边为对称轴作与它对称的图形.
②将得到的这组图形以一条边的中点为旋转中心旋转180 °.
③分别以这两组图形为平移的“基本图案”,各平移两次,即可得到最终的图形.
拓展与延伸
如图所示的图案是由一个梯形经过旋转和对称形成的,则该梯形应该满足什么条件?
解:该梯形的边应满足:上底等于腰且等于下底的一半;角应满足:四个内角分别为120°,120°,60°,60°.
布置作业
请完成对应习题
4 简单的图案设计
分析图案设计图案.(重点、难点)
学习目标
新课导入
问题:平移、轴对称变换、旋转有什么共同特征?
对称
左移
右移
新课讲解
知识点1 分析图案
观察下面的图案,分析它是将哪种基本图形经过了哪些变换后得到的?
将 经过旋转、
轴对称和平移得到的.
新课讲解
1.平面图案的形成依据:平移,旋转和轴对称.
2.图形的变换不改变图形的形状和大小,只改变
图形的位置.
新课讲解
3. 常见的变换类型有:
(1)平移变换;
(2)旋转变换;
(3)轴对称变换;
(4)旋转变换与平移变换的组合;
(5)旋转变换与轴对称变换的组合;
(6)轴对称变换与平移变换的组合.
新课讲解
例
典例分析
如图,在四个图案中,不能由基本图形旋转得到的是( )
D
新课讲解
分析:
寻找基本图形、旋转中心、旋转角、旋转次数,
逐一判断.A.可由一个基本“花瓣”绕其中心
经过7次旋转,每次旋转45°得到;B.可由一个
基本“菱形”绕其中心经过5次旋转,每次旋转
60°得到;C.可由一个基本图形绕其中心旋转
180°得到;D.不能由基本图形旋转得到.
新课讲解
练一练
如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形既是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有( )
A.2种 B.3种
C.4种 D.5种
C
新课讲解
知识点2 设计图案
图案设计的一般步骤:
(1)选择基本图案(基本图案可以是一个图案,也可
以是几个图案的结合).
(2)对基本图案进行变换(变换可以是单纯的平移,
旋转或轴对称,也可以是多种变换).
(3)对图案进行修饰.
新课讲解
例
典例分析
学校在艺术周上,要求学生制作一个精美的轴对称图形,请你用所给出的几何图形:○○△△--(两个圆,两个等边三角形,两条线段)为构件,构思一个独特、有意义的轴对称图形,并写上一句简要的解说词.
分析:
解答本例需要利用给定的六个元素,充分展开想
象的翅膀,组合成各种有意义的图形.此外,还
要有一定的生活经验和一定的文学修养.
新课讲解
所设计图形如图所示(答案不唯一,可供参考):
解:
新课讲解
例
典例分析
把如图所示图形中左上角的图案绕着中心O旋
转90°,180°,270°,画出你所得的图案.
新课讲解
分析:
根据旋转图形的特征,分别把如上图 (1)(2)(3)所
示图形中左上角的图案绕着中心O旋转90°,
180°,270°,点O的位置不动,其余各部分均
绕点O按相同的方向旋转90°,180°,270°,
据此可画出各图.
新课讲解
画出的图案如图所示.
解:
课堂小结
图案设计的一般步骤:
(1)选择基本图案(基本图案可以是一个图案,也可
以是几个图案的结合).
(2)对基本图案进行变换(变换可以是单纯的平移,
旋转或轴对称,也可以是多种变换).
(3)对图案进行修饰.
当堂小练
1.国旗上的四个小五角星,通过怎样的移动可以相互得到( )
A.轴对称 B.平移 C.旋转 D.平移和旋转
2.起重机将重物垂直提起,这可以看作为数学上的( )
A.轴对称 B.平移 C.旋转 D.变形
D
B
当堂小练
3.下图是由12个全等三角形组成的,利用平移、轴对称或旋转分析这个图案的形成过程.
当堂小练
解:这个图形可以按照以下步骤形成的.
①以一个三角形的一条边为对称轴作与它对称的图形.
②将得到的这组图形以一条边的中点为旋转中心旋转180 °.
③分别以这两组图形为平移的“基本图案”,各平移两次,即可得到最终的图形.
拓展与延伸
如图所示的图案是由一个梯形经过旋转和对称形成的,则该梯形应该满足什么条件?
解:该梯形的边应满足:上底等于腰且等于下底的一半;角应满足:四个内角分别为120°,120°,60°,60°.
布置作业
请完成对应习题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
