人教版九年级下册数学26.1.2 反比例函数的图像性质(1)同步课时习题(Word版含答案)
文档属性
| 名称 | 人教版九年级下册数学26.1.2 反比例函数的图像性质(1)同步课时习题(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 145.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 18:57:16 | ||
图片预览




文档简介
26.1.2
反比例函数的图像性质(1)
姓名:__________
分数:__________
?
1.
某反比例函数的图象经过点,则此函数图象也经过??
A.
B.
C.
D.
2.
设有反比例函数,、为其图象上的两点,若时,则的取值范围是(
)
A.
B.
C.
D.
3.
已知反比例函数为常数,的图象经过点,则当时,函数值的取值范围是(
)
A.
B.
C.
D.
4.
若点在反比例函数的图象上,则下列说法正确的是(
)
A.该函数图象分布在第二、四象限
B.的值为
C.该函数图象经过点
D.若点,都在该函数图象上,且,则
5.
一次函数,且随的增大而减小,那么反比例函数满足(
)
A.当时,
B.在每个象限内,随的增大而减小
C.图象分布在第一、三象限
D.图象分布在第二、四象限?
6.
函数=、、=中,当时,随增大而增大的函数共有(
)
A.个
B.个
C.个
D.个
7.
反比例函数(为不等于的常数)的图象如图所示,以下结论错误的是(
)
A.
B.若点在图象上,则=
C.在每个象限内,的值随值的增大而增大
D.若点,在图象上,则
8.
下列四个函数:①=;②=;③;④=.当时,随增大而增大的函数是(
)
A.①③④
B.②③④
C.②③
D.①④
9.
如图,菱形的边轴,垂足为点,顶点在第二象限,顶点在轴的正半轴上,反比例函数的图象同时经过顶点,.若点的横坐标为,=,则的值为(
)
A.
B.
C.
D.
10.
如图,在平面直角坐标系中,菱形的边在轴的正半轴上,反比例函数的图象经过对角线的中点和顶点.若菱形的面积为,则的值为(
)
A.
B.
C.
D.
二、填空题
11.
若反比例函数的图象经过点,则该反比例函数的图象在________象限.
12.
点在反比例函数的图象上,则________;在图象的每一个分支上,随的增大而________.
13.
在反比例函数的图象每一条曲线上,都随的增大而减小,则的取值范围是________.
14.
如图,,两点在双曲线的一个分支上,轴于点,垂直于轴于点,若的面积为,的面积为,则的值为________.
三、解答题
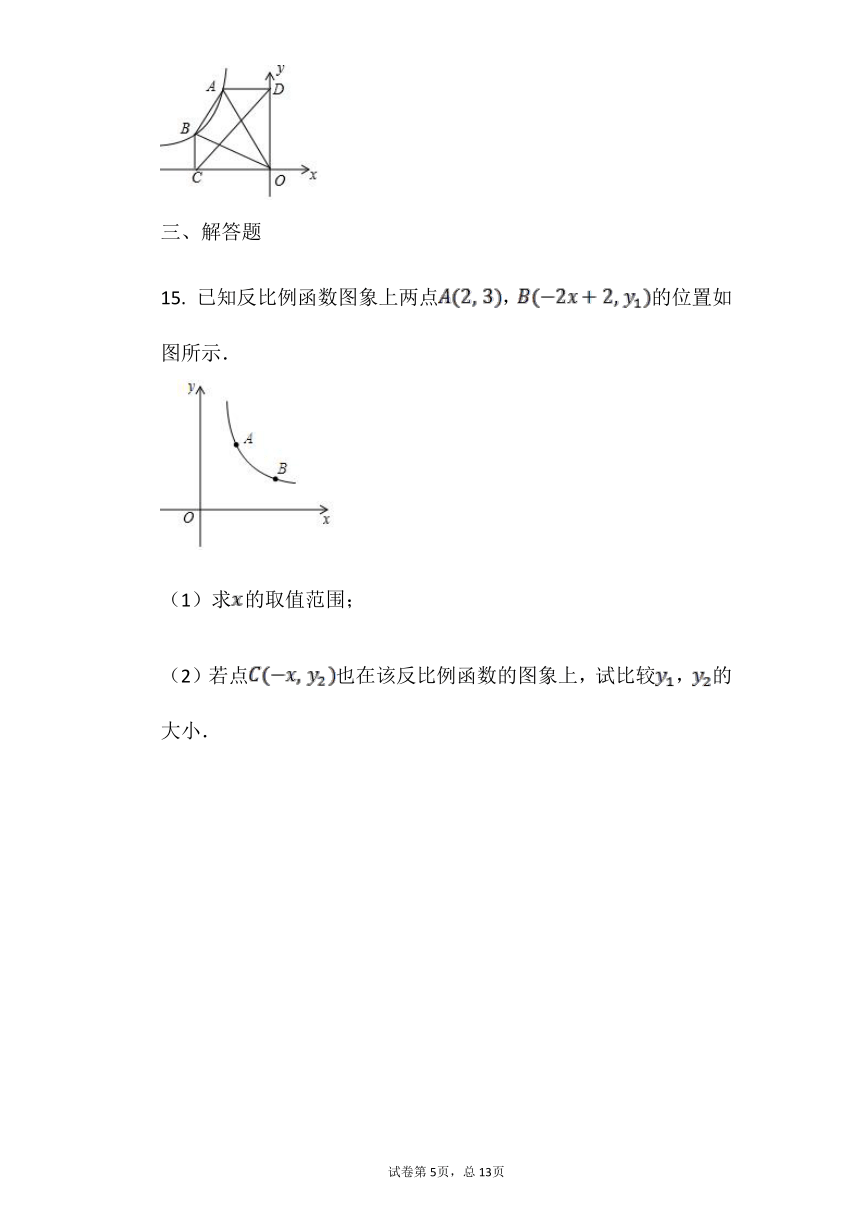
15.
已知反比例函数图象上两点,的位置如图所示.
(1)求的取值范围;
(2)若点也在该反比例函数的图象上,试比较,的大小.
?
16.
在平面直角坐标系中,反比例函数是常数,且的图象经过点.
(1)若=,求关于的函数表达式;
(2)点也在反比例函数的图象上:
①当且时,求的取值范围;
②若在第二象限,求证:.
?
17.
反比例函数的图象的一支位于第四象限.
图象的另一支位于第________象限;
常数的取值范围是什么?
在这个函数图象的某一支上任取点
和点,如果
,那么与有怎样的大小关系?
?
18.
已知反比例函数的图象经过点.
求反比例函数的表达式;
判断点是否在这个函数图象上,并说明理由;
当时,直接写出的取值范围.
参考答案
26.1.2
反比例函数的图像性质
一、
选择题
1.
【答案】A
2.
【答案】D
3.
【答案】D
4.
【答案】B
5.
【答案】D
6.
【答案】D
7.
【答案】C
8.
【答案】D
9.
【答案】C
10.
【答案】C
二、
填空题
11.
【答案】
二、四
12.
【答案】
,增大
13.
【答案】
14.
【答案】
三、
解答题
15.
【答案】
由反比例函数图象上两点,的位置可知,,
∴
;
∵
,
∴
,
∴
点在第一象限,
∵
=,
∴
,
∴
.
16.
【答案】
∵
=,
∴
,
∵
反比例函数是常数,且的图象经过点.
∴
==,
∴
;
①∵
反比例函数是常数,且的图象经过点,点也在反比例函数的图象上,
∴
=,
∴
=,
∵
且,
∴
,
解得且.
②∵
=,
∴
=,
∵
若在第二象限,
,
∴
,
∴
=
∴
.
17.
【答案】
二
∵
反比例函数的图象位于第二、四象限,
∴
,
解得:.
∵
,
∴
在函数图象的同一支上,随的增大而增大,
∴
当时,
.
18.
【答案】
解:∵
反比例函数的图象经过点,
∴
.
∴
反比例函数的表达式为.
∵
当时,,
∴
点不在这个函数的图象上.
当时,,
当时,.
∵
,∴
当时,随的增大而减小,
∴
当时,.
试卷第8页,总11页
试卷第7页,总11页
反比例函数的图像性质(1)
姓名:__________
分数:__________
?
1.
某反比例函数的图象经过点,则此函数图象也经过??
A.
B.
C.
D.
2.
设有反比例函数,、为其图象上的两点,若时,则的取值范围是(
)
A.
B.
C.
D.
3.
已知反比例函数为常数,的图象经过点,则当时,函数值的取值范围是(
)
A.
B.
C.
D.
4.
若点在反比例函数的图象上,则下列说法正确的是(
)
A.该函数图象分布在第二、四象限
B.的值为
C.该函数图象经过点
D.若点,都在该函数图象上,且,则
5.
一次函数,且随的增大而减小,那么反比例函数满足(
)
A.当时,
B.在每个象限内,随的增大而减小
C.图象分布在第一、三象限
D.图象分布在第二、四象限?
6.
函数=、、=中,当时,随增大而增大的函数共有(
)
A.个
B.个
C.个
D.个
7.
反比例函数(为不等于的常数)的图象如图所示,以下结论错误的是(
)
A.
B.若点在图象上,则=
C.在每个象限内,的值随值的增大而增大
D.若点,在图象上,则
8.
下列四个函数:①=;②=;③;④=.当时,随增大而增大的函数是(
)
A.①③④
B.②③④
C.②③
D.①④
9.
如图,菱形的边轴,垂足为点,顶点在第二象限,顶点在轴的正半轴上,反比例函数的图象同时经过顶点,.若点的横坐标为,=,则的值为(
)
A.
B.
C.
D.
10.
如图,在平面直角坐标系中,菱形的边在轴的正半轴上,反比例函数的图象经过对角线的中点和顶点.若菱形的面积为,则的值为(
)
A.
B.
C.
D.
二、填空题
11.
若反比例函数的图象经过点,则该反比例函数的图象在________象限.
12.
点在反比例函数的图象上,则________;在图象的每一个分支上,随的增大而________.
13.
在反比例函数的图象每一条曲线上,都随的增大而减小,则的取值范围是________.
14.
如图,,两点在双曲线的一个分支上,轴于点,垂直于轴于点,若的面积为,的面积为,则的值为________.
三、解答题
15.
已知反比例函数图象上两点,的位置如图所示.
(1)求的取值范围;
(2)若点也在该反比例函数的图象上,试比较,的大小.
?
16.
在平面直角坐标系中,反比例函数是常数,且的图象经过点.
(1)若=,求关于的函数表达式;
(2)点也在反比例函数的图象上:
①当且时,求的取值范围;
②若在第二象限,求证:.
?
17.
反比例函数的图象的一支位于第四象限.
图象的另一支位于第________象限;
常数的取值范围是什么?
在这个函数图象的某一支上任取点
和点,如果
,那么与有怎样的大小关系?
?
18.
已知反比例函数的图象经过点.
求反比例函数的表达式;
判断点是否在这个函数图象上,并说明理由;
当时,直接写出的取值范围.
参考答案
26.1.2
反比例函数的图像性质
一、
选择题
1.
【答案】A
2.
【答案】D
3.
【答案】D
4.
【答案】B
5.
【答案】D
6.
【答案】D
7.
【答案】C
8.
【答案】D
9.
【答案】C
10.
【答案】C
二、
填空题
11.
【答案】
二、四
12.
【答案】
,增大
13.
【答案】
14.
【答案】
三、
解答题
15.
【答案】
由反比例函数图象上两点,的位置可知,,
∴
;
∵
,
∴
,
∴
点在第一象限,
∵
=,
∴
,
∴
.
16.
【答案】
∵
=,
∴
,
∵
反比例函数是常数,且的图象经过点.
∴
==,
∴
;
①∵
反比例函数是常数,且的图象经过点,点也在反比例函数的图象上,
∴
=,
∴
=,
∵
且,
∴
,
解得且.
②∵
=,
∴
=,
∵
若在第二象限,
,
∴
,
∴
=
∴
.
17.
【答案】
二
∵
反比例函数的图象位于第二、四象限,
∴
,
解得:.
∵
,
∴
在函数图象的同一支上,随的增大而增大,
∴
当时,
.
18.
【答案】
解:∵
反比例函数的图象经过点,
∴
.
∴
反比例函数的表达式为.
∵
当时,,
∴
点不在这个函数的图象上.
当时,,
当时,.
∵
,∴
当时,随的增大而减小,
∴
当时,.
试卷第8页,总11页
试卷第7页,总11页
