人教版数学七年级下册5.1相交线专项训练(Word版 含答案)
文档属性
| 名称 | 人教版数学七年级下册5.1相交线专项训练(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 138.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 19:08:42 | ||
图片预览

文档简介
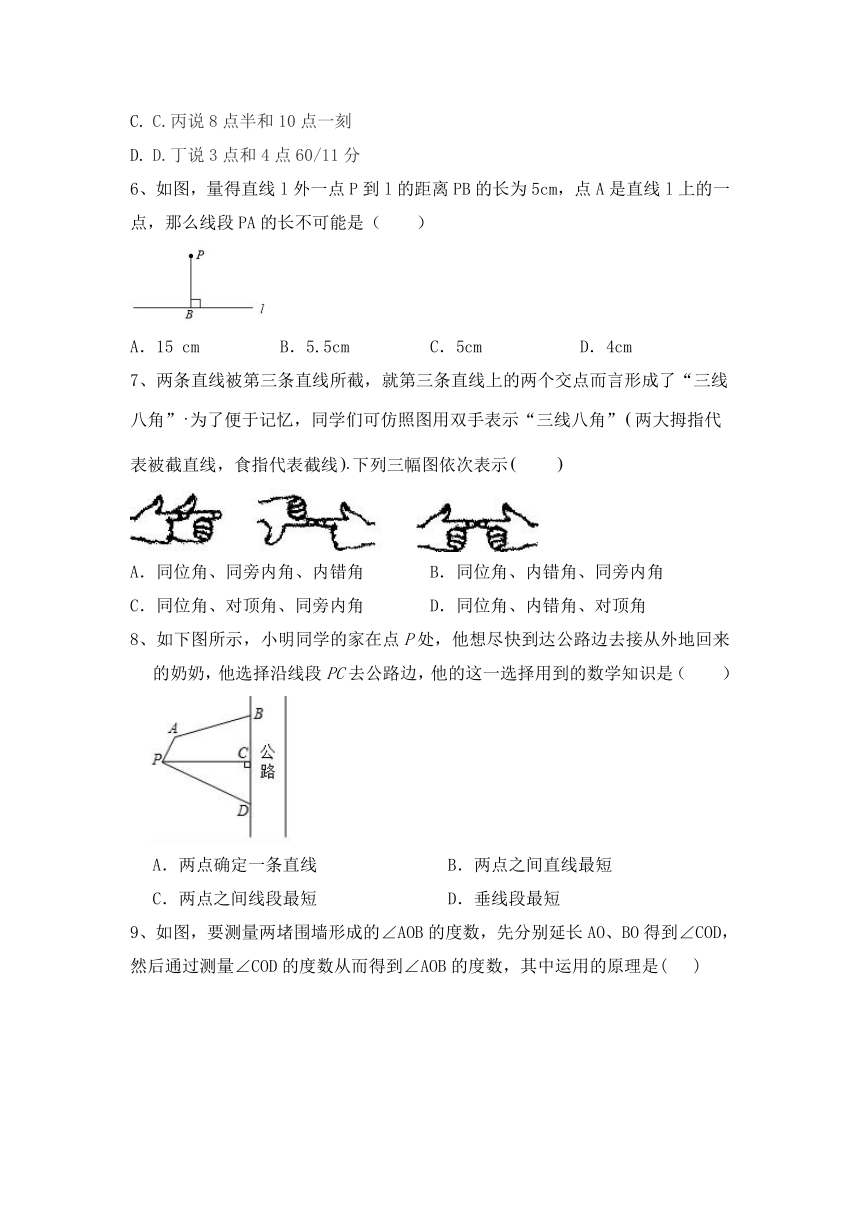
人教版七年级下册数学5.1相交线专项训练
选择。
1、下列图形中与是同位角的是(
)
A.
B.
C.
D.
2、下列图形,与不是邻补角的是(
)
A.
B.
C.
D.
3、如图,∠BAC=90°,AD⊥BC于点D,点C到AD的距离是下列哪条线段的长度( )
A.AC
B.BC
C.CD
D.AD
4、如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,则图中能表示点到直线距离的垂线段共有
A.2条
B.3条
C.4条
D.5条
甲、乙、丙、丁四位学生在判断时钟的时针与分针互相垂直的时刻,他们每个人说了两个时刻,说对的是()
A.甲说3点和3点半
乙说6点和6点15分
C.丙说8点半和10点一刻
D.丁说3点和4点60/11分
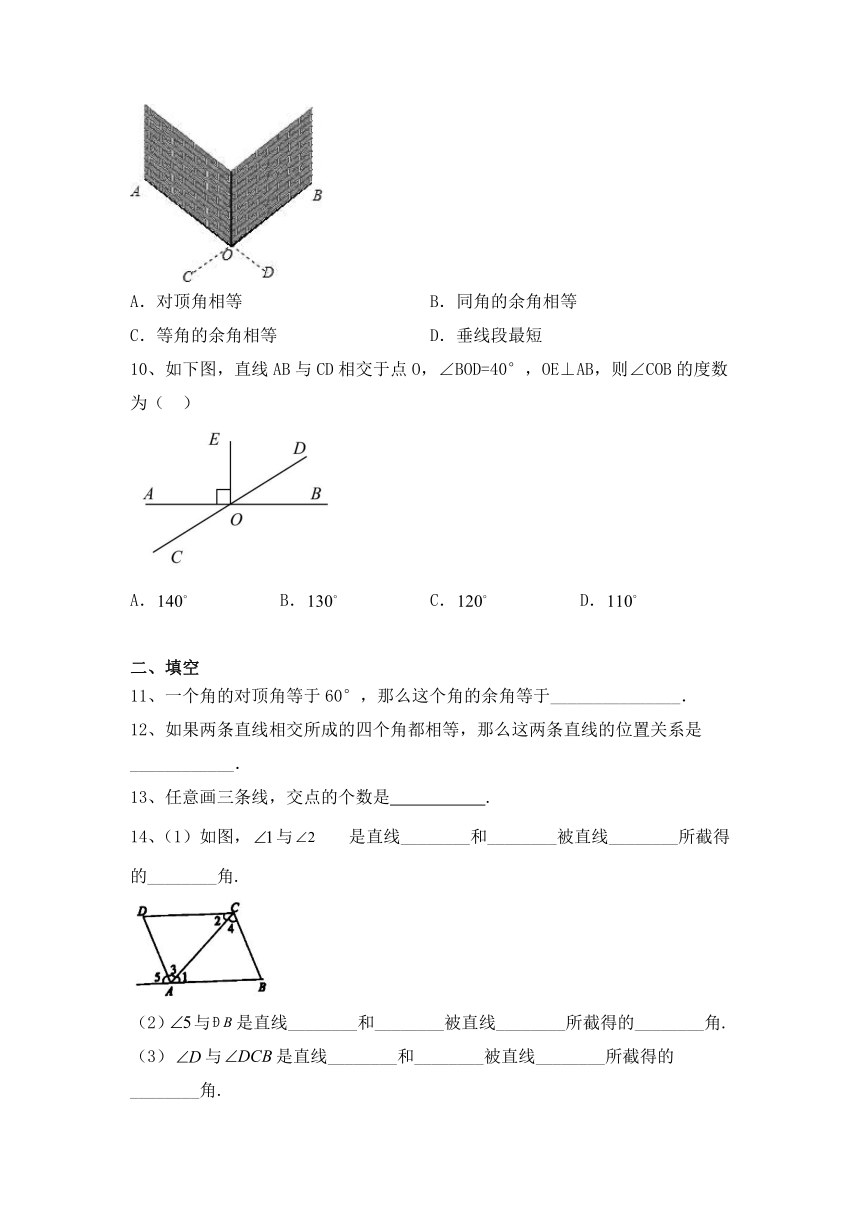
6、如图,量得直线l外一点P到l的距离PB的长为5cm,点A是直线l上的一点,那么线段PA的长不可能是( )
A.15
cm
B.5.5cm
C.5cm
D.4cm
7、两条直线被第三条直线所截,就第三条直线上的两个交点而言形成了“三线八角”为了便于记忆,同学们可仿照图用双手表示“三线八角”两大拇指代表被截直线,食指代表截线下列三幅图依次表示
A.同位角、同旁内角、内错角
B.同位角、内错角、同旁内角
C.同位角、对顶角、同旁内角
D.同位角、内错角、对顶角
8、如下图所示,小明同学的家在点P处,他想尽快到达公路边去接从外地回来的奶奶,他选择沿线段PC去公路边,他的这一选择用到的数学知识是( )
A.两点确定一条直线
B.两点之间直线最短
C.两点之间线段最短
D.垂线段最短
9、如图,要测量两堵围墙形成的∠AOB的度数,先分别延长AO、BO得到∠COD,然后通过测量∠COD的度数从而得到∠AOB的度数,其中运用的原理是(
)
A.对顶角相等
B.同角的余角相等
C.等角的余角相等
D.垂线段最短
10、如下图,直线AB与CD相交于点O,∠BOD=40°,OE⊥AB,则∠COB的度数为(
)
A.
B.
C.
D.
二、填空
11、一个角的对顶角等于60°,那么这个角的余角等于_______________.
12、如果两条直线相交所成的四个角都相等,那么这两条直线的位置关系是____________.
13、任意画三条线,交点的个数是
.
14、(1)如图,与是直线________和________被直线________所截得的________角.
(2)与是直线________和________被直线________所截得的________角.
(3)与是直线________和________被直线________所截得的________角.
三、解答。
15、如图,已知∠DAB=65°,∠1=∠C.
(1)在图中画出∠DAB的对顶角;
(2)写出∠1的同位角;
(3)写出∠C的同旁内角.
16、如图,点P,点Q分别代表两个村庄,直线l代表两个村庄中间的一条公路.根据居民出行的需要,计划在公路l上的某处设置一个公交站.
(1)若考虑到村庄P居住的老年人较多,计划建一个离村庄P最近的车站,请在公路l上画出车站的位置(用点M表示),依据是
;
(2)若考虑到修路的费用问题,希望车站的位置到村庄P和村庄Q的距离之和最小,请在公路l上画出车站的位置(用点N表示),依据是
.
17、复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想.
(1)如图1,直线,被直线所截,在这个基本图形中,形成了______对同旁内角.
(2)如图2,平面内三条直线,,两两相交,交点分别为、、,图中一共有______对同旁内角.
(3)平面内四条直线两两相交,最多可以形成______对同旁内角.
(4)平面内条直线两两相交,最多可以形成______对同旁内角.
答案
C
2、C
3、C
4、A
5、D
D
7、B
8、C
9、A
10、A
11、30°
垂直
不能确定
略
(1)略;(2)∠1的同位角是∠DAB;(3)∠C的同旁内角是∠B和∠ADC.
16、(1)如图,点M即为所示.依据是直线外一点与直线上各点连接的所有线段中垂线段最短
(2)如图,点N即为所示.依据是两点之间线段最短;
故答案为:直线外一点与直线上各点连接的所有线段中垂线段最短;两点之间线段最短.
17、(1)2;(2)6;(3)24;(4)
选择。
1、下列图形中与是同位角的是(
)
A.
B.
C.
D.
2、下列图形,与不是邻补角的是(
)
A.
B.
C.
D.
3、如图,∠BAC=90°,AD⊥BC于点D,点C到AD的距离是下列哪条线段的长度( )
A.AC
B.BC
C.CD
D.AD
4、如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,则图中能表示点到直线距离的垂线段共有
A.2条
B.3条
C.4条
D.5条
甲、乙、丙、丁四位学生在判断时钟的时针与分针互相垂直的时刻,他们每个人说了两个时刻,说对的是()
A.甲说3点和3点半
乙说6点和6点15分
C.丙说8点半和10点一刻
D.丁说3点和4点60/11分
6、如图,量得直线l外一点P到l的距离PB的长为5cm,点A是直线l上的一点,那么线段PA的长不可能是( )
A.15
cm
B.5.5cm
C.5cm
D.4cm
7、两条直线被第三条直线所截,就第三条直线上的两个交点而言形成了“三线八角”为了便于记忆,同学们可仿照图用双手表示“三线八角”两大拇指代表被截直线,食指代表截线下列三幅图依次表示
A.同位角、同旁内角、内错角
B.同位角、内错角、同旁内角
C.同位角、对顶角、同旁内角
D.同位角、内错角、对顶角
8、如下图所示,小明同学的家在点P处,他想尽快到达公路边去接从外地回来的奶奶,他选择沿线段PC去公路边,他的这一选择用到的数学知识是( )
A.两点确定一条直线
B.两点之间直线最短
C.两点之间线段最短
D.垂线段最短
9、如图,要测量两堵围墙形成的∠AOB的度数,先分别延长AO、BO得到∠COD,然后通过测量∠COD的度数从而得到∠AOB的度数,其中运用的原理是(
)
A.对顶角相等
B.同角的余角相等
C.等角的余角相等
D.垂线段最短
10、如下图,直线AB与CD相交于点O,∠BOD=40°,OE⊥AB,则∠COB的度数为(
)
A.
B.
C.
D.
二、填空
11、一个角的对顶角等于60°,那么这个角的余角等于_______________.
12、如果两条直线相交所成的四个角都相等,那么这两条直线的位置关系是____________.
13、任意画三条线,交点的个数是
.
14、(1)如图,与是直线________和________被直线________所截得的________角.
(2)与是直线________和________被直线________所截得的________角.
(3)与是直线________和________被直线________所截得的________角.
三、解答。
15、如图,已知∠DAB=65°,∠1=∠C.
(1)在图中画出∠DAB的对顶角;
(2)写出∠1的同位角;
(3)写出∠C的同旁内角.
16、如图,点P,点Q分别代表两个村庄,直线l代表两个村庄中间的一条公路.根据居民出行的需要,计划在公路l上的某处设置一个公交站.
(1)若考虑到村庄P居住的老年人较多,计划建一个离村庄P最近的车站,请在公路l上画出车站的位置(用点M表示),依据是
;
(2)若考虑到修路的费用问题,希望车站的位置到村庄P和村庄Q的距离之和最小,请在公路l上画出车站的位置(用点N表示),依据是
.
17、复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想.
(1)如图1,直线,被直线所截,在这个基本图形中,形成了______对同旁内角.
(2)如图2,平面内三条直线,,两两相交,交点分别为、、,图中一共有______对同旁内角.
(3)平面内四条直线两两相交,最多可以形成______对同旁内角.
(4)平面内条直线两两相交,最多可以形成______对同旁内角.
答案
C
2、C
3、C
4、A
5、D
D
7、B
8、C
9、A
10、A
11、30°
垂直
不能确定
略
(1)略;(2)∠1的同位角是∠DAB;(3)∠C的同旁内角是∠B和∠ADC.
16、(1)如图,点M即为所示.依据是直线外一点与直线上各点连接的所有线段中垂线段最短
(2)如图,点N即为所示.依据是两点之间线段最短;
故答案为:直线外一点与直线上各点连接的所有线段中垂线段最短;两点之间线段最短.
17、(1)2;(2)6;(3)24;(4)
