_人教版七年级下册5.3.1平行线的性质教案
文档属性
| 名称 | _人教版七年级下册5.3.1平行线的性质教案 |  | |
| 格式 | zip | ||
| 文件大小 | 857.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-26 22:13:02 | ||
图片预览


文档简介
长沙市明德天心中学统一备课用纸
科
目
数学
年
级
七年级
班
级
授课时间
年
月
日
课
题
5.3.1
平行线的性质
课
型
新授课
教学目标
理解平行线的性质,会利用平行线的性质求角的度数。
能利用性质1推导性质2,3,体会数学化归思想方法。
能正确区分平行线的判定和性质,能进行简单的推理说明;
教学重点
平行线的性质
教学难点
区分平行线的判定方法和性质
教具准备
多媒体及课件
教学内容及过程
教学方法
一、知识回顾
①∵∠1=∠C
∴__//__(
)
②
∵∠1=∠B
∴
__
//
__(
)
③
∵∠2+∠B=180°
∴
__
//
__(
)
判定:数量关系→位置关系
二、思考探究
问题
通过上题可知平行线的判定方法是什么?
思考
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
探究:利用坐标纸上的直线或者用直尺和三角尺画两条平行线a∥b,然后,画一条截线c与这两条平行线相交,标出这些角.
度量这些角,把结果填入下表:
角∠1∠2∠3∠4度数角∠5∠6∠7∠8度数
各对同位角、内错角、同旁内角的度数之间有什么关系?写出你的猜想.
两条平行线被第三条直线所截,同位角_____;内错角______;同旁内角_______.
再任意画一条截线d,同样度量并计算各个角的度数,你的猜想还成立吗?
(利用几何画板演示)
揭示内涵,得出性质
一般地,平行线具有如下性质:
性质1:两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
几何语言:
∵a∥b(已知)
∴∠1=∠2
(两直线平行,同位角相等)
1.如图,已知a//b,那么?2与?3相等吗?为什么?
性质2:两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
几何语言:
∵a∥b(已知)
∴∠2=∠3(两直线平行,内错角相等)
2.如图,已知a//b,那么∠2与∠4有什么关系呢?为什么?
性质3:两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
几何语言:
∵a∥b(已知)
∴∠2+∠4=180
°(两直线平行,内错角相等)
3.如图,直线AB∥CD,则下列结论正确的是( )
A.∠1=∠2
B.∠3=∠4
C.∠1+∠3=180°
D.∠3+∠4=180
4.如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边上.若∠2=44°,那么∠1的度数是( )
A.14°
B.15°
C.16°
D.17°
5.如图,已知AD∥BC,∠B=30°,DB平分∠ADE,则∠CED是(
)
A.30°
B.40°
C.50°
D.60°
6.判断:①两直线被第三条直线所截,同位角相等.
②两直线平行,同旁内角相等.
③“内错角相等,两直线平行”是平行线的性质.
④“两直线平行,同旁内角互补”是平行线的性质.
7.如图:∵∠1=∠2( )
∴AD∥ ( )
∴∠BCD+ =180°( )
四、典例分析
例1
如图是一块梯形铁片的残余部分,量得∠A
=100°,∠B
=115°,
梯形的另外两个角是多少度?为什么?
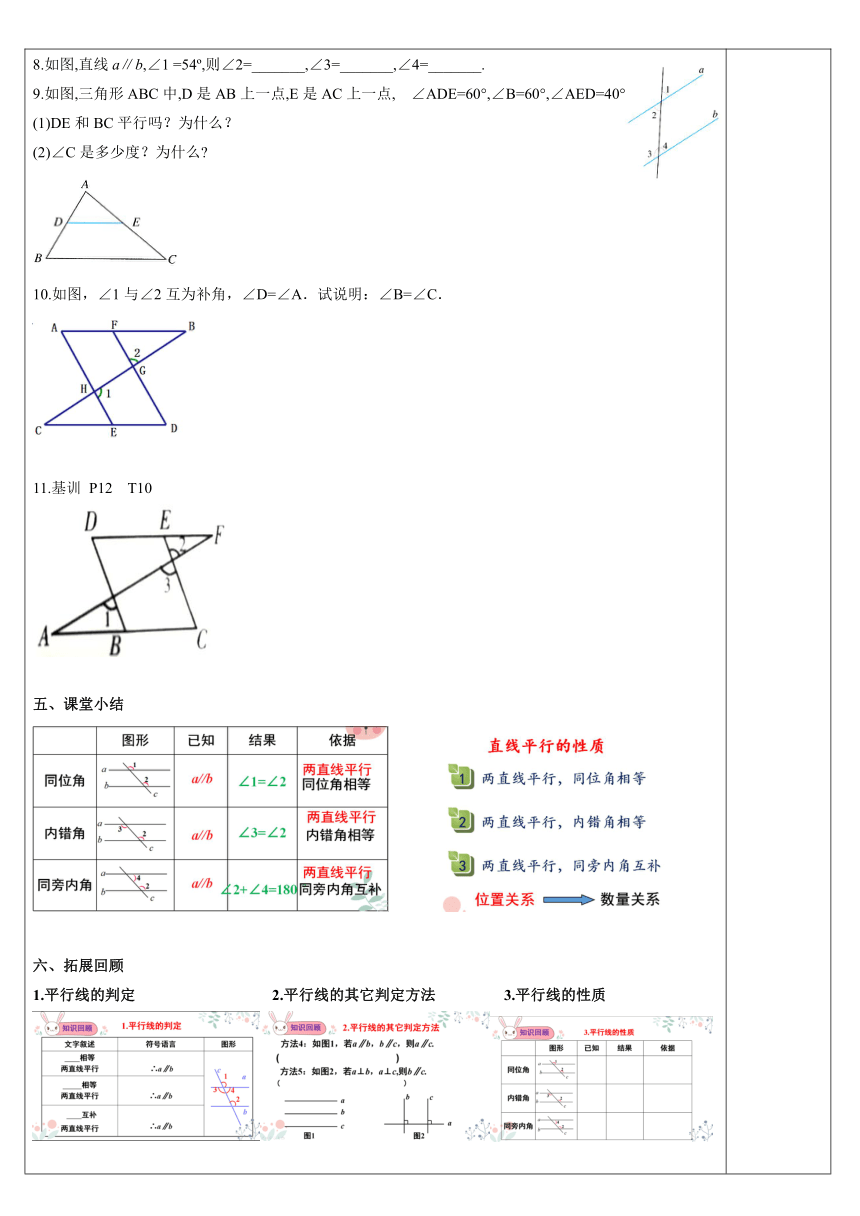
8.如图,直线a∥b,∠1
=54?,则∠2=_______,∠3=_______,∠4=_______.
9.如图,三角形ABC中,D是AB上一点,E是AC上一点,
∠ADE=60°,∠B=60°,∠AED=40°.
(1)DE和BC平行吗?为什么?
(2)∠C是多少度?为什么?
10.如图,∠1与∠2互为补角,∠D=∠A.试说明:∠B=∠C.
11.基训
P12
T10
五、课堂小结
六、拓展回顾
1.平行线的判定
2.平行线的其它判定方法
3.平行线的性质
七、拓展典例
例
如图
①
∵
∠1
=_____(已知)
∴
AB∥CE(
)
②
∵
∠1
+_____=180o(已知)
∴
CD∥BF(
)
③
∵
∠1
+∠5
=180o(已知)
∴
_____∥_____.(
)
④
∵
∠4
+_____=180o(已知)
∴
CE∥AB(
)
练习:已知∠3=45
°,∠1与∠2互余,试说明AB//CD.
八、拓展练习
1.已知AB⊥BF,CD⊥BF,∠1=
∠2,试说明∠3=∠E.
2.如图,EF∥AD,∠1=∠2,∠BAC=70
°,求∠AGD的度数.
3.如图,直线AB//CD,E在AB与CD之间,且∠B=61°,∠D=34°.①求∠BED的度数.
②写出∠BED和∠B、∠D的数量关系
1、添加适当的平行线,将要求的角转化为两个平行线间所夹的内错角、同位角或者同旁内角来解答.
2、自己添加的线叫做辅助线,用虚线表示.
变式:已知AB∥CD,任意三角形3个内角的和都是180°,请分别写出下列四个图形中∠APC和∠A、∠C的关系,并选择图(1)、(2)之一说明理由.
5.拓展提升:如图,AB//CD,试解决下列问题:
(1)如图1,∠1+∠2=________;
(2)如图2,∠1+∠2+∠3=________;
(3)如图3,∠1+∠2+∠3+∠4=________;
(4)如图4,试探究∠1+∠2+∠3+∠4+…+∠n=________;
6.拓展提升:如图,AB//CD,试解决下列问题:
(1)如图1,∠A+∠C=__________;
(2)如图2,∠A+∠F=________;
(3)如图3,∠A+∠F1+∠C=________;
(4)如图4,试探究∠A+∠F1+∠F2+∠F3+…+∠Fn=________;
教
学
反
思
科
目
数学
年
级
七年级
班
级
授课时间
年
月
日
课
题
5.3.1
平行线的性质
课
型
新授课
教学目标
理解平行线的性质,会利用平行线的性质求角的度数。
能利用性质1推导性质2,3,体会数学化归思想方法。
能正确区分平行线的判定和性质,能进行简单的推理说明;
教学重点
平行线的性质
教学难点
区分平行线的判定方法和性质
教具准备
多媒体及课件
教学内容及过程
教学方法
一、知识回顾
①∵∠1=∠C
∴__//__(
)
②
∵∠1=∠B
∴
__
//
__(
)
③
∵∠2+∠B=180°
∴
__
//
__(
)
判定:数量关系→位置关系
二、思考探究
问题
通过上题可知平行线的判定方法是什么?
思考
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
探究:利用坐标纸上的直线或者用直尺和三角尺画两条平行线a∥b,然后,画一条截线c与这两条平行线相交,标出这些角.
度量这些角,把结果填入下表:
角∠1∠2∠3∠4度数角∠5∠6∠7∠8度数
各对同位角、内错角、同旁内角的度数之间有什么关系?写出你的猜想.
两条平行线被第三条直线所截,同位角_____;内错角______;同旁内角_______.
再任意画一条截线d,同样度量并计算各个角的度数,你的猜想还成立吗?
(利用几何画板演示)
揭示内涵,得出性质
一般地,平行线具有如下性质:
性质1:两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
几何语言:
∵a∥b(已知)
∴∠1=∠2
(两直线平行,同位角相等)
1.如图,已知a//b,那么?2与?3相等吗?为什么?
性质2:两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
几何语言:
∵a∥b(已知)
∴∠2=∠3(两直线平行,内错角相等)
2.如图,已知a//b,那么∠2与∠4有什么关系呢?为什么?
性质3:两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
几何语言:
∵a∥b(已知)
∴∠2+∠4=180
°(两直线平行,内错角相等)
3.如图,直线AB∥CD,则下列结论正确的是( )
A.∠1=∠2
B.∠3=∠4
C.∠1+∠3=180°
D.∠3+∠4=180
4.如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边上.若∠2=44°,那么∠1的度数是( )
A.14°
B.15°
C.16°
D.17°
5.如图,已知AD∥BC,∠B=30°,DB平分∠ADE,则∠CED是(
)
A.30°
B.40°
C.50°
D.60°
6.判断:①两直线被第三条直线所截,同位角相等.
②两直线平行,同旁内角相等.
③“内错角相等,两直线平行”是平行线的性质.
④“两直线平行,同旁内角互补”是平行线的性质.
7.如图:∵∠1=∠2( )
∴AD∥ ( )
∴∠BCD+ =180°( )
四、典例分析
例1
如图是一块梯形铁片的残余部分,量得∠A
=100°,∠B
=115°,
梯形的另外两个角是多少度?为什么?
8.如图,直线a∥b,∠1
=54?,则∠2=_______,∠3=_______,∠4=_______.
9.如图,三角形ABC中,D是AB上一点,E是AC上一点,
∠ADE=60°,∠B=60°,∠AED=40°.
(1)DE和BC平行吗?为什么?
(2)∠C是多少度?为什么?
10.如图,∠1与∠2互为补角,∠D=∠A.试说明:∠B=∠C.
11.基训
P12
T10
五、课堂小结
六、拓展回顾
1.平行线的判定
2.平行线的其它判定方法
3.平行线的性质
七、拓展典例
例
如图
①
∵
∠1
=_____(已知)
∴
AB∥CE(
)
②
∵
∠1
+_____=180o(已知)
∴
CD∥BF(
)
③
∵
∠1
+∠5
=180o(已知)
∴
_____∥_____.(
)
④
∵
∠4
+_____=180o(已知)
∴
CE∥AB(
)
练习:已知∠3=45
°,∠1与∠2互余,试说明AB//CD.
八、拓展练习
1.已知AB⊥BF,CD⊥BF,∠1=
∠2,试说明∠3=∠E.
2.如图,EF∥AD,∠1=∠2,∠BAC=70
°,求∠AGD的度数.
3.如图,直线AB//CD,E在AB与CD之间,且∠B=61°,∠D=34°.①求∠BED的度数.
②写出∠BED和∠B、∠D的数量关系
1、添加适当的平行线,将要求的角转化为两个平行线间所夹的内错角、同位角或者同旁内角来解答.
2、自己添加的线叫做辅助线,用虚线表示.
变式:已知AB∥CD,任意三角形3个内角的和都是180°,请分别写出下列四个图形中∠APC和∠A、∠C的关系,并选择图(1)、(2)之一说明理由.
5.拓展提升:如图,AB//CD,试解决下列问题:
(1)如图1,∠1+∠2=________;
(2)如图2,∠1+∠2+∠3=________;
(3)如图3,∠1+∠2+∠3+∠4=________;
(4)如图4,试探究∠1+∠2+∠3+∠4+…+∠n=________;
6.拓展提升:如图,AB//CD,试解决下列问题:
(1)如图1,∠A+∠C=__________;
(2)如图2,∠A+∠F=________;
(3)如图3,∠A+∠F1+∠C=________;
(4)如图4,试探究∠A+∠F1+∠F2+∠F3+…+∠Fn=________;
教
学
反
思
