人教版数学七年级下册 5.2.1《平行线》讲学稿(无答案)
文档属性
| 名称 | 人教版数学七年级下册 5.2.1《平行线》讲学稿(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 123.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 00:00:00 | ||
图片预览

文档简介
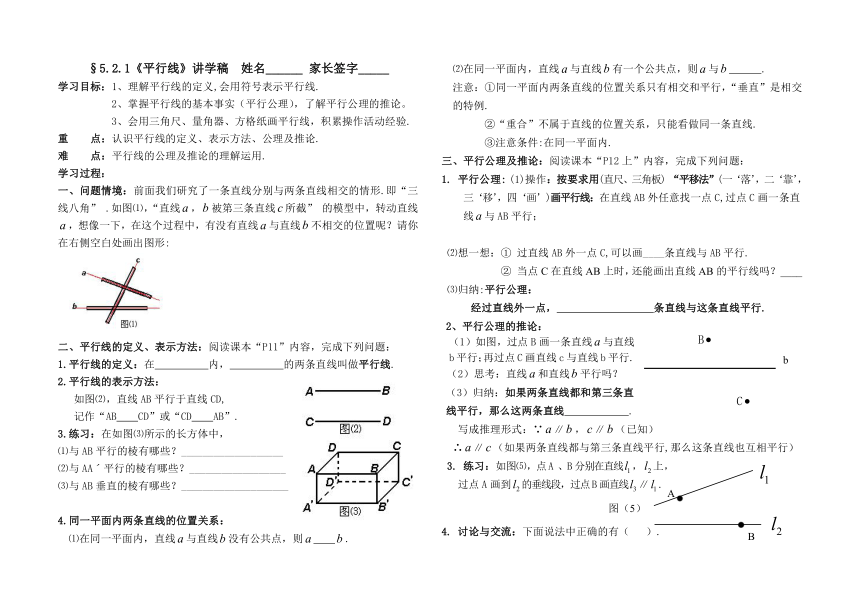
§5.2.1《平行线》讲学稿
姓名______
家长签字_____
学习目标:1、理解平行线的定义,会用符号表示平行线.
2、掌握平行线的基本事实(平行公理),了解平行公理的推论。
3、会用三角尺、量角器、方格纸画平行线,积累操作活动经验.
重
点:认识平行线的定义、表示方法、公理及推论.
难
点:平行线的公理及推论的理解运用.
学习过程:
一、问题情境:前面我们研究了一条直线分别与两条直线相交的情形.即“三线八角”
.如图⑴,“直线,被第三条直线所截”
的模型中,转动直线,想像一下,在这个过程中,有没有直线与直线不相交的位置呢?请你在右侧空白处画出图形:
二、平行线的定义、表示方法:阅读课本“P11”内容,完成下列问题:
1.平行线的定义:在
内,
的两条直线叫做平行线.
2.平行线的表示方法:
如图⑵,直线AB平行于直线CD,
记作“AB
CD”或“CD
AB”.
3.练习:在如图⑶所示的长方体中,
⑴与AB平行的棱有哪些?___________________
⑵与AAˊ平行的棱有哪些?__________________
⑶与AB垂直的棱有哪些?____________________
4.同一平面内两条直线的位置关系:
⑴在同一平面内,直线与直线没有公共点,则
.
⑵在同一平面内,直线与直线有一个公共点,则与
.
注意:①同一平面内两条直线的位置关系只有相交和平行,“垂直”是相交的特例.
②“重合”不属于直线的位置关系,只能看做同一条直线.
③注意条件:在同一平面内.
三、平行公理及推论:阅读课本“P12上”内容,完成下列问题:
1.
平行公理:
(1)操作:按要求用(直尺、三角板)
“平移法”(一‘落’,二‘靠’,三‘移’,四‘画’)画平行线:在直线AB外任意找一点C,过点C画一条直线与AB平行;
⑵想一想:①
过直线AB外一点C,可以画____条直线与AB平行.
②
当点C在直线AB上时,还能画出直线AB的平行线吗?____
⑶归纳:平行公理:
经过直线外一点,
条直线与这条直线平行.
2、平行公理的推论:
(1)如图,过点B画一条直线与直线b平行;再过点C画直线c与直线b平行.
(2)思考:直线和直线平行吗?
(3)归纳:如果两条直线都和第三条直线平行,那么这两条直线
.
写成推理形式:∵∥,∥(已知)
∴∥(如果两条直线都与第三条直线平行,那么这条直线也互相平行)
3.
练习:如图⑸,点A
、B分别在直线,上,
过点A画到的垂线段,过点B画直线∥.
4.
讨论与交流:下面说法中正确的有(
).
一条直线的平行线只有一条;
过一点与已知直线平行的直线只有一条;
③因为∥,∥,所以∥;
④经过直线外一点,有且只有一条直线与这条直线平行.
四、课堂小结:
同一平面内两条
直线的位置关系
五、课堂检测:
⒈判断下列说法是否正确,并说明理由.
⑴不相交的两条直线是平行线;(
)
⑵没有公共点的两条线段一定平行;(
)
⑶在同一平面内两条直线不平行就一定相交;(
)
⑷不相交的两条射线一定平行;(
)
⑸两条线段平行,实际上是指它们所在的直线平行.(
)
⒉是平面上三条直线,交点可能有(
)个
A、1
B、1或2或3
C、0或1或2或3
D、以上都不对.
⒊读下列语句,按要求作图:
(1)点P是直线AB外一点,直线CD
经过点P,且与直线AB平行;
(2)直线AB、CD是相交直线,点P
是直线AB、CD外的一点,直线EF经
过点P且与直线AB平行,与直线CD
相交于点E。
六、课后作业
1、跟踪训练:
(1)同一平面内,如果两条直线都和第三条直线相交,那么这两条直线(
)
A、平行
B、相交
C、平行或相交
D、重合.
(2)直线同侧有A、B、C三点,如果A、B两点确定的直线与B、C两点确定的直线都与直线平行,则A、B、C三点的位置关系是
,其理由依据是
.
(3)如图,在5×5的网格中,AC是网格中最长的线段,请画出两条线段
与AC平行并且过网格的格点.
(4)如图,过点C画CE∥AD交BA的延长线于E.
2、P18习题5.2
“11”
观察如图所示的长方体,用符号表示
下列两棱的位置关系:
A1B1____AB,
AA1____AB,
A1D1____C1D1,
AD_____BC.
3、如图⑹,如果AE∥BC,AD∥BC,那么∠DAE=180°,为什么?
解:∵AE∥BC,AD∥BC(已知)
∴AE、AD在同一直线上
(经过直线外一点,有且只有
一
条直线与这条直线平行)
∴∠DAE=180°(平角的定义)
教学后记:
姓名______
家长签字_____
学习目标:1、理解平行线的定义,会用符号表示平行线.
2、掌握平行线的基本事实(平行公理),了解平行公理的推论。
3、会用三角尺、量角器、方格纸画平行线,积累操作活动经验.
重
点:认识平行线的定义、表示方法、公理及推论.
难
点:平行线的公理及推论的理解运用.
学习过程:
一、问题情境:前面我们研究了一条直线分别与两条直线相交的情形.即“三线八角”
.如图⑴,“直线,被第三条直线所截”
的模型中,转动直线,想像一下,在这个过程中,有没有直线与直线不相交的位置呢?请你在右侧空白处画出图形:
二、平行线的定义、表示方法:阅读课本“P11”内容,完成下列问题:
1.平行线的定义:在
内,
的两条直线叫做平行线.
2.平行线的表示方法:
如图⑵,直线AB平行于直线CD,
记作“AB
CD”或“CD
AB”.
3.练习:在如图⑶所示的长方体中,
⑴与AB平行的棱有哪些?___________________
⑵与AAˊ平行的棱有哪些?__________________
⑶与AB垂直的棱有哪些?____________________
4.同一平面内两条直线的位置关系:
⑴在同一平面内,直线与直线没有公共点,则
.
⑵在同一平面内,直线与直线有一个公共点,则与
.
注意:①同一平面内两条直线的位置关系只有相交和平行,“垂直”是相交的特例.
②“重合”不属于直线的位置关系,只能看做同一条直线.
③注意条件:在同一平面内.
三、平行公理及推论:阅读课本“P12上”内容,完成下列问题:
1.
平行公理:
(1)操作:按要求用(直尺、三角板)
“平移法”(一‘落’,二‘靠’,三‘移’,四‘画’)画平行线:在直线AB外任意找一点C,过点C画一条直线与AB平行;
⑵想一想:①
过直线AB外一点C,可以画____条直线与AB平行.
②
当点C在直线AB上时,还能画出直线AB的平行线吗?____
⑶归纳:平行公理:
经过直线外一点,
条直线与这条直线平行.
2、平行公理的推论:
(1)如图,过点B画一条直线与直线b平行;再过点C画直线c与直线b平行.
(2)思考:直线和直线平行吗?
(3)归纳:如果两条直线都和第三条直线平行,那么这两条直线
.
写成推理形式:∵∥,∥(已知)
∴∥(如果两条直线都与第三条直线平行,那么这条直线也互相平行)
3.
练习:如图⑸,点A
、B分别在直线,上,
过点A画到的垂线段,过点B画直线∥.
4.
讨论与交流:下面说法中正确的有(
).
一条直线的平行线只有一条;
过一点与已知直线平行的直线只有一条;
③因为∥,∥,所以∥;
④经过直线外一点,有且只有一条直线与这条直线平行.
四、课堂小结:
同一平面内两条
直线的位置关系
五、课堂检测:
⒈判断下列说法是否正确,并说明理由.
⑴不相交的两条直线是平行线;(
)
⑵没有公共点的两条线段一定平行;(
)
⑶在同一平面内两条直线不平行就一定相交;(
)
⑷不相交的两条射线一定平行;(
)
⑸两条线段平行,实际上是指它们所在的直线平行.(
)
⒉是平面上三条直线,交点可能有(
)个
A、1
B、1或2或3
C、0或1或2或3
D、以上都不对.
⒊读下列语句,按要求作图:
(1)点P是直线AB外一点,直线CD
经过点P,且与直线AB平行;
(2)直线AB、CD是相交直线,点P
是直线AB、CD外的一点,直线EF经
过点P且与直线AB平行,与直线CD
相交于点E。
六、课后作业
1、跟踪训练:
(1)同一平面内,如果两条直线都和第三条直线相交,那么这两条直线(
)
A、平行
B、相交
C、平行或相交
D、重合.
(2)直线同侧有A、B、C三点,如果A、B两点确定的直线与B、C两点确定的直线都与直线平行,则A、B、C三点的位置关系是
,其理由依据是
.
(3)如图,在5×5的网格中,AC是网格中最长的线段,请画出两条线段
与AC平行并且过网格的格点.
(4)如图,过点C画CE∥AD交BA的延长线于E.
2、P18习题5.2
“11”
观察如图所示的长方体,用符号表示
下列两棱的位置关系:
A1B1____AB,
AA1____AB,
A1D1____C1D1,
AD_____BC.
3、如图⑹,如果AE∥BC,AD∥BC,那么∠DAE=180°,为什么?
解:∵AE∥BC,AD∥BC(已知)
∴AE、AD在同一直线上
(经过直线外一点,有且只有
一
条直线与这条直线平行)
∴∠DAE=180°(平角的定义)
教学后记:
