苏科版数学七年级下册 第7章《平面图像的认识(二)》单元综合训练卷(Word版 含解析)
文档属性
| 名称 | 苏科版数学七年级下册 第7章《平面图像的认识(二)》单元综合训练卷(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 235.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 00:00:00 | ||
图片预览


文档简介
七年级第二学期数学苏科版第7章《平面图像的认识(二)》单元综合训练卷
一、单选题
1.如图,能判断直线AB∥CD的条件是(
)
A.
B.
C.
D.
2.如图,某地域的江水经过B、C、D三点处拐弯后,水流的方向与原来相同,若∠ABC=125°,∠BCD=75°,则∠CDE的度数为(
)
A.20°
B.25°
C.35°
D.50°
3.如图,A,B,C,D中的哪幅图案可以通过图案①平移得到( )
A.
B.
C.
D.
4.如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是(
)
A.B.
C.
D.
5.如图,三角形ABC中,AB=AC,D,E分别为边AB,AC上的点,DM平分∠BDE,EN平分∠DEC,若∠DMN=110°,则∠DEA=( )
A.40°
B.50°
C.60°
D.70°
6.如图,直线a∥b,将一直角三角形的直角顶点置于直线b上,若∠1=28°,则∠2的度数是( )
A.62°
B.108°
C.118°
D.152°
7.将一张长方形纸片折叠成如图所示的形状,则∠ABC等于( )
A.73°
B.56°
C.68°
D.146°
8.如图,已知∠BOF=120°,则∠A+∠B+∠C+∠D+∠E+∠F为多少度( )
A.360°
B.720°
C.540°
D.240°
9.如图,直线CE∥DF,∠CAB=125°,∠ABD=85°,则∠ECA+∠BDF=( )
A.30°
B.35°
C.36°
D.40°
10.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )
A.∠A=∠1+∠2
B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2
D.3∠A=2(∠1+∠2)
二、填空题
11.已知三条不同的直线a、b、c在同一平面内,下列四条命题:
①如果a∥b,a⊥c,那么b⊥c;
②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c;④如果b⊥a,c⊥a,那么b∥c.
其中真命题的是__________.(填写所有真命题的序号)
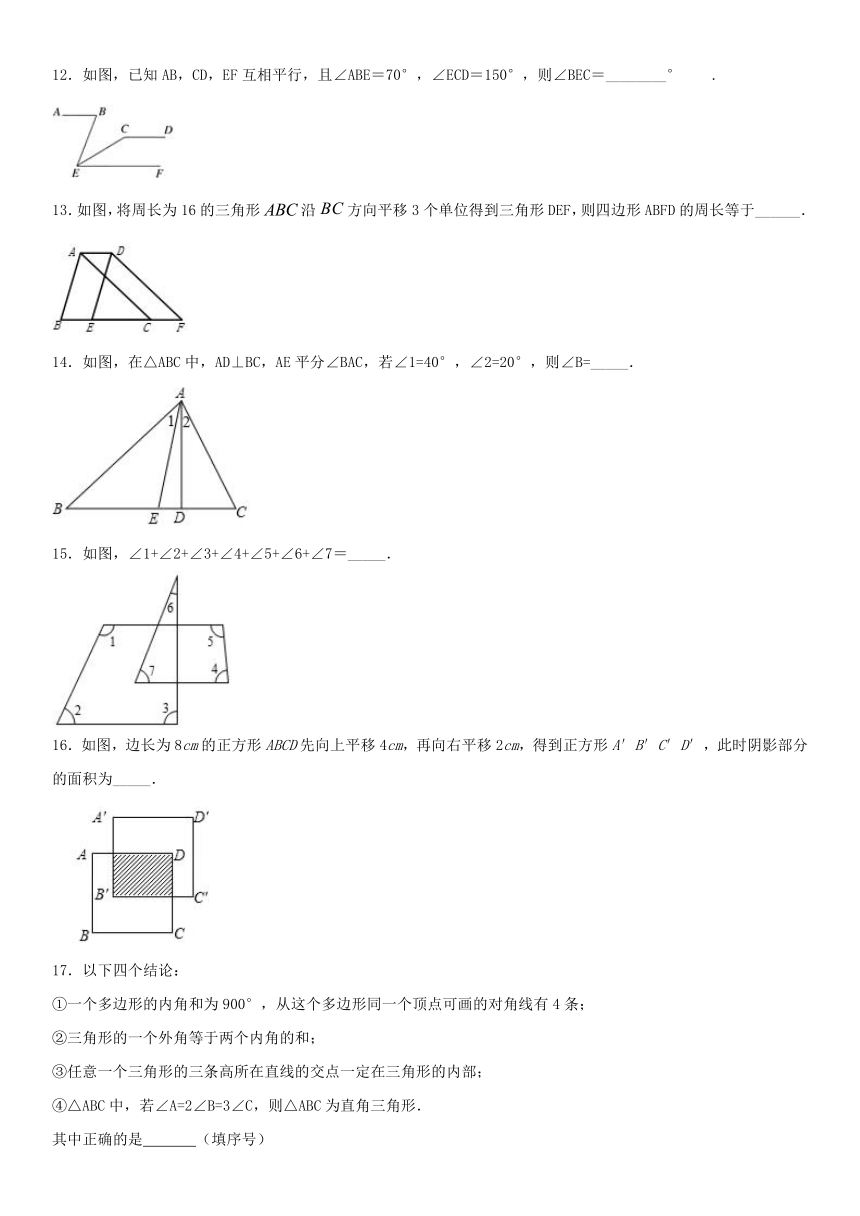
12.如图,已知AB,CD,EF互相平行,且∠ABE=70°,∠ECD=150°,则∠BEC=________°.
13.如图,将周长为16的三角形沿方向平移3个单位得到三角形DEF,则四边形ABFD的周长等于______.
14.如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=40°,∠2=20°,则∠B=_____.
15.如图,∠1+∠2+∠3+∠4+∠5+∠6+∠7=_____.
16.如图,边长为8cm的正方形ABCD先向上平移4cm,再向右平移2cm,得到正方形A′B′C′D′,此时阴影部分的面积为_____.
17.以下四个结论:
①一个多边形的内角和为900°,从这个多边形同一个顶点可画的对角线有4条;
②三角形的一个外角等于两个内角的和;
③任意一个三角形的三条高所在直线的交点一定在三角形的内部;
④△ABC中,若∠A=2∠B=3∠C,则△ABC为直角三角形.
其中正确的是
(填序号)
三、解答题
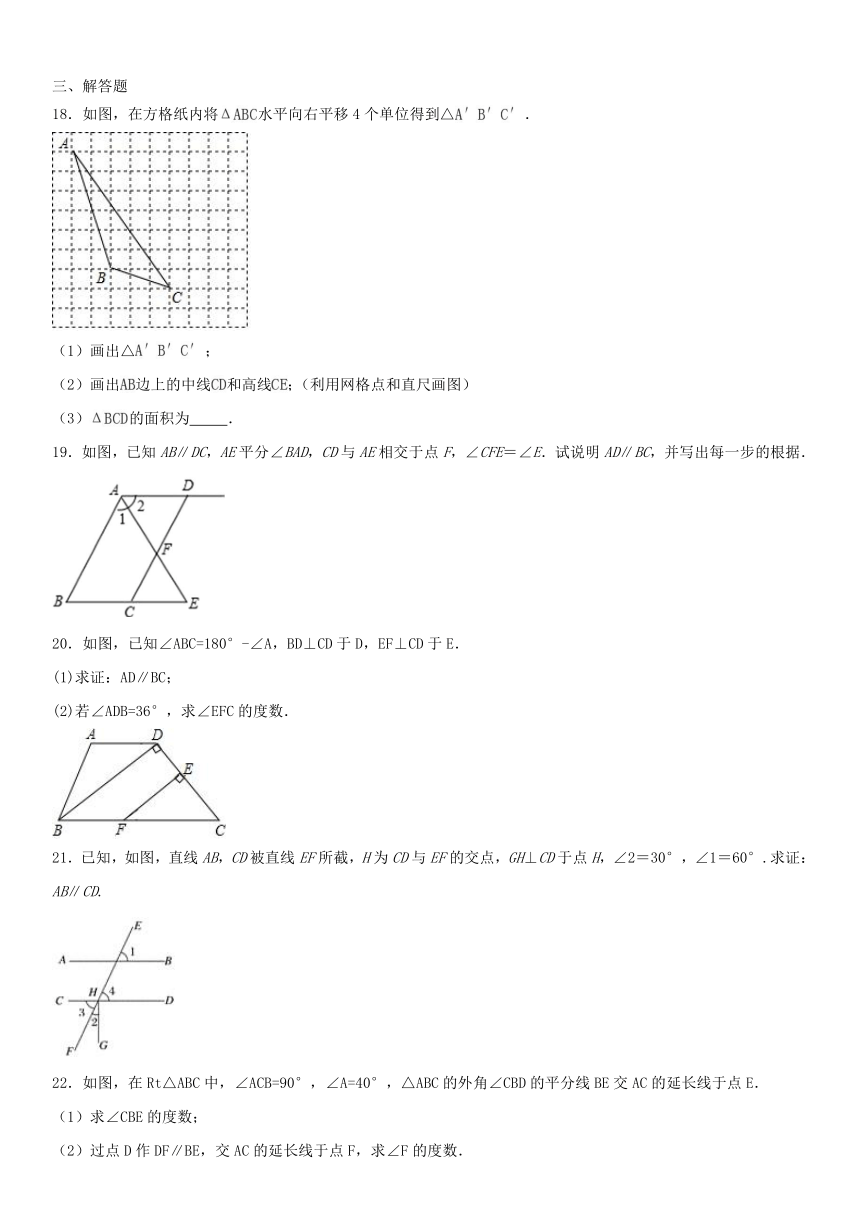
18.如图,在方格纸内将水平向右平移4个单位得到△.
(1)画出△;
(2)画出边上的中线和高线;(利用网格点和直尺画图)
(3)的面积为
.
19.如图,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC,并写出每一步的根据.
20.如图,已知∠ABC=180°-∠A,BD⊥CD于D,EF⊥CD于E.
(1)求证:AD∥BC;
(2)若∠ADB=36°,求∠EFC的度数.
21.已知,如图,直线AB,CD被直线EF所截,H为CD与EF的交点,GH⊥CD于点H,∠2=30°,∠1=60°.求证:AB∥CD.
22.如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
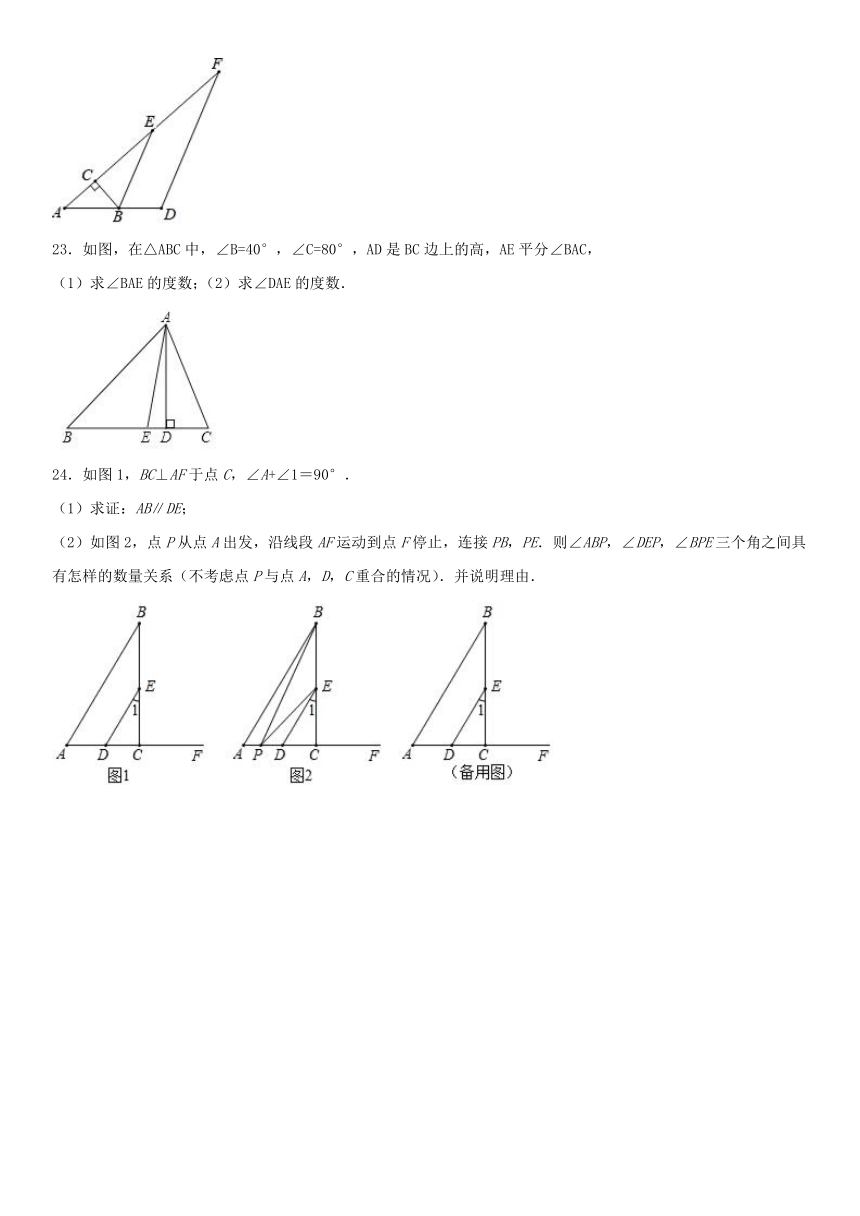
23.如图,在△ABC中,∠B=40°,∠C=80°,AD是BC边上的高,AE平分∠BAC,
(1)求∠BAE的度数;(2)求∠DAE的度数.
24.如图1,BC⊥AF于点C,∠A+∠1=90°.
(1)求证:AB∥DE;
(2)如图2,点P从点A出发,沿线段AF运动到点F停止,连接PB,PE.则∠ABP,∠DEP,∠BPE三个角之间具有怎样的数量关系(不考虑点P与点A,D,C重合的情况).并说明理由.
试卷第1页,总3页
参考答案
1.A
A选项中∠3和∠4的对顶角是一组同旁内角,所以当∠3+∠4=180°时AB∥CD;
B选项中∠3和∠4的对顶角是一组同旁内角,所以当∠3=∠4时AB与CD不一定平行;
C选项中∠1和∠3的对顶角是一组同旁内角,所以当∠1+∠3=180°时,AB与CD不一定平行;
D选项中∠1和∠2的对顶角是一组同旁内角,所以当∠1=∠2时AB与CD不一定平行.
2.A
解:由题意得,AB∥DE,
如图,过点C作CF∥AB,则CF∥DE,
∴∠BCF+∠ABC=180°,
∴∠BCF=180°-125°=55°,
∴∠DCF=75°-55°=20°,
∴∠CDE=∠DCF=20°.
3.D
通过图案①平移得到必须与图案①完全相同,角度也必须相同,
观察图形可知D可以通过图案①平移得到.
4.A
根据定义可得A是作BC边上的高,C是作AB边上的高,D是作AC边上的高.
5.A
解:∵AB=AC,
∴∠B=∠C,
又∵DM平分∠BDE,EN平分∠DEC,
∴∠BDM=∠EDM,∠CEN=∠DEN,
∵∠B=∠DMN-∠BDM=∠DMN-∠EDM,
∠C=∠ENM-∠CEN=∠ENM-∠DEN,
∴∠DMN-∠EDM=∠ENM-∠DEN,即∠DMN+∠DEN=∠EDM+∠ENM,
∵四边形DMNE内角和为360°,
∴∠DMN+∠DEN=∠EDM+∠ENM=180°,
∴∠DEN=70°,
则∠DEA=180°-2∠DEN=40°.
6.C
如图,∵AB∥CD,
∴∠2=∠ABC=∠1+∠CBE=28°+90°=118°,
7.A
∵∠CBD=34°,
∴∠CBE=180°﹣∠CBD=146°,
由折叠的性质可得
∠ABC=∠ABE=∠CBE=73°.
8.D
如图,
根据三角形的外角性质,∠1=∠A+∠C,∠2=∠B+∠D,
∵∠BOF=120°,
∴∠3=180°﹣120°=60°,
根据三角形内角和定理,∠E+∠1=180°﹣60°=120°,
∠F+∠2=180°﹣60°=120°,
所以,∠1+∠2+∠E+∠F=120°+120°=240°,
即∠A+∠B+∠C+∠D+∠E+∠F=240°.
9.A
如图,∵CE∥DF,
∴∠CEA+∠F=180°,
∵∠CAB=125°,∠ABD=85°,
∴∠1+∠CEA=∠CAB=125°,∠2+∠F=∠ABD=85°,
∴∠1+∠2=∠CAB+∠ABD﹣(∠CEA+∠F)=30°.
10.B
∵在四边形ADA′E中,∠A+∠A′+∠ADA′+∠AEA′=360°,
则2∠A+(180°-∠2)+(180°-∠1)=360°,
∴可得2∠A=∠1+∠2.
11.①②④.
①如果a∥b,a⊥c,那么b⊥c是真命题,故本选项正确,
②如果b∥a,c∥a,那么b∥c是真命题,故本选项正确,
③如果b⊥a,c⊥a,那么b⊥c是假命题,故本选项错误,
④如果b⊥a,c⊥a,那么b∥c是真命题,故本选项正确,
12.40
解:∵AB∥EF,
∴∠BEF=∠ABE=70°;
又∵EF∥CD,
∴∠CEF=180°-∠ECD=180°-150°=30°,
∴∠BEC=∠BEF-∠CEF=40°;
13.22
解:∵△ABC沿BC方向平移3个单位得△DEF,∴AD=CF=3,AC=DF.
∵△ABC的周长等于16,∴AB+BC+AC=16,∴四边形ABFD的周长=AB+BF+DF+AD
=AB+BC+CF+AC+AD=16+3+3=22.
14.30°
∵AE平分∠BAC,
∴∠1=∠EAD+∠2,
∴∠EAD=∠1﹣∠2=40°﹣20°=20°,
∵AD⊥BC,
∴∠ADB=90°,
Rt△ABD中,∠B=90°﹣∠BAD=90°﹣40°﹣20°=30°,
15.540°
如下图,由三角形的外角性质可知∠6+∠7=∠8,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+∠2+∠3+∠4+∠5+∠8,
又∵∠1+∠2+∠3+∠10=360°,
∠4+∠5+∠8+∠9=360°,∠10+∠9=180°,
∴∠1+∠2+∠3+∠4+∠5+∠8=(∠1+∠2+∠3+∠10)+(∠4+∠5+∠8+∠9)-(∠10+∠9)=540°.
16.24cm2
∵边长为8cm的正方形ABCD先向上平移4cm,
∴阴影部分的长为8﹣4=4m,
∵向右平移2cm,
∴阴影部分的宽为8﹣2=6cm,
∴阴影部分的面积为6×4=24cm2.
故答案为:24cm2.
17.①
结论①:设该多边形的边数为n
(n为正整数且n>2),则,解得n=7.
因为从n边形(n为正整数且n>2)的同一个顶点最多可画(n-3)条对角线,
所以从这个多边形同一个顶点可画的对角线有7-3=4(条).故结论①正确.
结论②:因为三角形的一个外角等于与它不相邻的两个内角的和,而不是任意两个内角之和,故结论②错误.
结论③:如图,△ABC为钝角三角形.
在△ABC中,三条高所在直线(即直线AD,BE,CF)的交点G在三角形外部,故结论③错误.
结论④:设∠A=(6x)°,根据∠A=2∠B=3∠C,则∠B=(3x)°,∠C=(2x)°.
在△ABC中,6x+3x+2x=11x=180,∴,
∴∠A,∠B,∠C均不等于90°.∴△ABC不是直角三角形.故结论④错误.
综上所述,正确的结论只有结论①.故本题应填写:①
.
18.
(1)如图所示:
(2)如图所示;
(3)S△BCD=20-5-1-10=4.
19.
证明:∵AB∥DC(已知)
∴∠1=∠CFE(两直线平行,同位角相等)
∵AE平分∠BAD(已知)
∴∠1=∠2(角平分线的定义)
∴∠CFE=∠2(等量代换)
∵∠CFE=∠E(已知)
∴∠2=∠E(等量代换)
∴AD∥BC(内错角相等,两直线平行).
20.
(1)证明:∵∠ABC=180°-∠A,
∴∠ABC+∠A=180°,
∴AD∥BC;
(2)∵AD∥BC,∠ADB=36°,
∴∠DBC=∠ADB=36°,
∵BD⊥CD,EF⊥CD,
∴BD∥EF,
∴∠DBC=∠EFC=36°
21.
∵GH⊥CD,
∴∠CHG=90°.
又∵∠2=30°,
∴∠3=60°.
∴∠4=60°.
又∵∠1=60°,
∴∠1=∠4.
∴AB∥CD(同位角相等,两直线平行).
22.
(1)∵在Rt△ABC中,∠ACB=90°,∠A=40°,
∴∠ABC=90°﹣∠A=50°,
∴∠CBD=130°.
∵BE是∠CBD的平分线,
∴∠CBE=∠CBD=65°;
(2)∵∠ACB=90°,∠CBE=65°,
∴∠CEB=90°﹣65°=25°.
∵DF∥BE,
∴∠F=∠CEB=25°.
23.
(1)∵在△ABC中,∠ABC=40°,∠ACB=80°,
∴∠BAC=180°-40°-80°=60°,
∵AE平分∠BAC,
∴∠BAE=30°;
(2)∵AD是△ABC的高,
∴∠ADB=90°,
∴∠BAD=180°-90°-40°=50°,
∴∠DAE=∠BAD-∠BAE=50°-30°=20°.
24.
解:(1)如图1,∵BC⊥AF于点C,
∴∠A+∠B=90°,
又∵∠A+∠1=90°,
∴∠B=∠1,
∴AB∥DE.
(2)如图2,当点P在A,D之间时,过P作PG∥AB,
∵AB∥DE,
∴PG∥DE,
∴∠ABP=∠GPB,∠DEP=∠GPE,
∴∠BPE=∠BPG+∠EPG=∠ABP+∠DEP;
如图所示,当点P在C,D之间时,过P作PG∥AB,
∵AB∥DE,
∴PG∥DE,
∴∠ABP=∠GPB,∠DEP=∠GPE,
∴∠BPE=∠BPG﹣∠EPG=∠ABP﹣∠DEP;
如图所示,当点P在C,F之间时,过P作PG∥AB,
∵AB∥DE,
∴PG∥DE,
∴∠ABP=∠GPB,∠DEP=∠GPE,
∴∠BPE=∠EPG﹣∠BPG=∠DEP﹣∠ABP.
一、单选题
1.如图,能判断直线AB∥CD的条件是(
)
A.
B.
C.
D.
2.如图,某地域的江水经过B、C、D三点处拐弯后,水流的方向与原来相同,若∠ABC=125°,∠BCD=75°,则∠CDE的度数为(
)
A.20°
B.25°
C.35°
D.50°
3.如图,A,B,C,D中的哪幅图案可以通过图案①平移得到( )
A.
B.
C.
D.
4.如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是(
)
A.B.
C.
D.
5.如图,三角形ABC中,AB=AC,D,E分别为边AB,AC上的点,DM平分∠BDE,EN平分∠DEC,若∠DMN=110°,则∠DEA=( )
A.40°
B.50°
C.60°
D.70°
6.如图,直线a∥b,将一直角三角形的直角顶点置于直线b上,若∠1=28°,则∠2的度数是( )
A.62°
B.108°
C.118°
D.152°
7.将一张长方形纸片折叠成如图所示的形状,则∠ABC等于( )
A.73°
B.56°
C.68°
D.146°
8.如图,已知∠BOF=120°,则∠A+∠B+∠C+∠D+∠E+∠F为多少度( )
A.360°
B.720°
C.540°
D.240°
9.如图,直线CE∥DF,∠CAB=125°,∠ABD=85°,则∠ECA+∠BDF=( )
A.30°
B.35°
C.36°
D.40°
10.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )
A.∠A=∠1+∠2
B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2
D.3∠A=2(∠1+∠2)
二、填空题
11.已知三条不同的直线a、b、c在同一平面内,下列四条命题:
①如果a∥b,a⊥c,那么b⊥c;
②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c;④如果b⊥a,c⊥a,那么b∥c.
其中真命题的是__________.(填写所有真命题的序号)
12.如图,已知AB,CD,EF互相平行,且∠ABE=70°,∠ECD=150°,则∠BEC=________°.
13.如图,将周长为16的三角形沿方向平移3个单位得到三角形DEF,则四边形ABFD的周长等于______.
14.如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=40°,∠2=20°,则∠B=_____.
15.如图,∠1+∠2+∠3+∠4+∠5+∠6+∠7=_____.
16.如图,边长为8cm的正方形ABCD先向上平移4cm,再向右平移2cm,得到正方形A′B′C′D′,此时阴影部分的面积为_____.
17.以下四个结论:
①一个多边形的内角和为900°,从这个多边形同一个顶点可画的对角线有4条;
②三角形的一个外角等于两个内角的和;
③任意一个三角形的三条高所在直线的交点一定在三角形的内部;
④△ABC中,若∠A=2∠B=3∠C,则△ABC为直角三角形.
其中正确的是
(填序号)
三、解答题
18.如图,在方格纸内将水平向右平移4个单位得到△.
(1)画出△;
(2)画出边上的中线和高线;(利用网格点和直尺画图)
(3)的面积为
.
19.如图,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC,并写出每一步的根据.
20.如图,已知∠ABC=180°-∠A,BD⊥CD于D,EF⊥CD于E.
(1)求证:AD∥BC;
(2)若∠ADB=36°,求∠EFC的度数.
21.已知,如图,直线AB,CD被直线EF所截,H为CD与EF的交点,GH⊥CD于点H,∠2=30°,∠1=60°.求证:AB∥CD.
22.如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
23.如图,在△ABC中,∠B=40°,∠C=80°,AD是BC边上的高,AE平分∠BAC,
(1)求∠BAE的度数;(2)求∠DAE的度数.
24.如图1,BC⊥AF于点C,∠A+∠1=90°.
(1)求证:AB∥DE;
(2)如图2,点P从点A出发,沿线段AF运动到点F停止,连接PB,PE.则∠ABP,∠DEP,∠BPE三个角之间具有怎样的数量关系(不考虑点P与点A,D,C重合的情况).并说明理由.
试卷第1页,总3页
参考答案
1.A
A选项中∠3和∠4的对顶角是一组同旁内角,所以当∠3+∠4=180°时AB∥CD;
B选项中∠3和∠4的对顶角是一组同旁内角,所以当∠3=∠4时AB与CD不一定平行;
C选项中∠1和∠3的对顶角是一组同旁内角,所以当∠1+∠3=180°时,AB与CD不一定平行;
D选项中∠1和∠2的对顶角是一组同旁内角,所以当∠1=∠2时AB与CD不一定平行.
2.A
解:由题意得,AB∥DE,
如图,过点C作CF∥AB,则CF∥DE,
∴∠BCF+∠ABC=180°,
∴∠BCF=180°-125°=55°,
∴∠DCF=75°-55°=20°,
∴∠CDE=∠DCF=20°.
3.D
通过图案①平移得到必须与图案①完全相同,角度也必须相同,
观察图形可知D可以通过图案①平移得到.
4.A
根据定义可得A是作BC边上的高,C是作AB边上的高,D是作AC边上的高.
5.A
解:∵AB=AC,
∴∠B=∠C,
又∵DM平分∠BDE,EN平分∠DEC,
∴∠BDM=∠EDM,∠CEN=∠DEN,
∵∠B=∠DMN-∠BDM=∠DMN-∠EDM,
∠C=∠ENM-∠CEN=∠ENM-∠DEN,
∴∠DMN-∠EDM=∠ENM-∠DEN,即∠DMN+∠DEN=∠EDM+∠ENM,
∵四边形DMNE内角和为360°,
∴∠DMN+∠DEN=∠EDM+∠ENM=180°,
∴∠DEN=70°,
则∠DEA=180°-2∠DEN=40°.
6.C
如图,∵AB∥CD,
∴∠2=∠ABC=∠1+∠CBE=28°+90°=118°,
7.A
∵∠CBD=34°,
∴∠CBE=180°﹣∠CBD=146°,
由折叠的性质可得
∠ABC=∠ABE=∠CBE=73°.
8.D
如图,
根据三角形的外角性质,∠1=∠A+∠C,∠2=∠B+∠D,
∵∠BOF=120°,
∴∠3=180°﹣120°=60°,
根据三角形内角和定理,∠E+∠1=180°﹣60°=120°,
∠F+∠2=180°﹣60°=120°,
所以,∠1+∠2+∠E+∠F=120°+120°=240°,
即∠A+∠B+∠C+∠D+∠E+∠F=240°.
9.A
如图,∵CE∥DF,
∴∠CEA+∠F=180°,
∵∠CAB=125°,∠ABD=85°,
∴∠1+∠CEA=∠CAB=125°,∠2+∠F=∠ABD=85°,
∴∠1+∠2=∠CAB+∠ABD﹣(∠CEA+∠F)=30°.
10.B
∵在四边形ADA′E中,∠A+∠A′+∠ADA′+∠AEA′=360°,
则2∠A+(180°-∠2)+(180°-∠1)=360°,
∴可得2∠A=∠1+∠2.
11.①②④.
①如果a∥b,a⊥c,那么b⊥c是真命题,故本选项正确,
②如果b∥a,c∥a,那么b∥c是真命题,故本选项正确,
③如果b⊥a,c⊥a,那么b⊥c是假命题,故本选项错误,
④如果b⊥a,c⊥a,那么b∥c是真命题,故本选项正确,
12.40
解:∵AB∥EF,
∴∠BEF=∠ABE=70°;
又∵EF∥CD,
∴∠CEF=180°-∠ECD=180°-150°=30°,
∴∠BEC=∠BEF-∠CEF=40°;
13.22
解:∵△ABC沿BC方向平移3个单位得△DEF,∴AD=CF=3,AC=DF.
∵△ABC的周长等于16,∴AB+BC+AC=16,∴四边形ABFD的周长=AB+BF+DF+AD
=AB+BC+CF+AC+AD=16+3+3=22.
14.30°
∵AE平分∠BAC,
∴∠1=∠EAD+∠2,
∴∠EAD=∠1﹣∠2=40°﹣20°=20°,
∵AD⊥BC,
∴∠ADB=90°,
Rt△ABD中,∠B=90°﹣∠BAD=90°﹣40°﹣20°=30°,
15.540°
如下图,由三角形的外角性质可知∠6+∠7=∠8,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+∠2+∠3+∠4+∠5+∠8,
又∵∠1+∠2+∠3+∠10=360°,
∠4+∠5+∠8+∠9=360°,∠10+∠9=180°,
∴∠1+∠2+∠3+∠4+∠5+∠8=(∠1+∠2+∠3+∠10)+(∠4+∠5+∠8+∠9)-(∠10+∠9)=540°.
16.24cm2
∵边长为8cm的正方形ABCD先向上平移4cm,
∴阴影部分的长为8﹣4=4m,
∵向右平移2cm,
∴阴影部分的宽为8﹣2=6cm,
∴阴影部分的面积为6×4=24cm2.
故答案为:24cm2.
17.①
结论①:设该多边形的边数为n
(n为正整数且n>2),则,解得n=7.
因为从n边形(n为正整数且n>2)的同一个顶点最多可画(n-3)条对角线,
所以从这个多边形同一个顶点可画的对角线有7-3=4(条).故结论①正确.
结论②:因为三角形的一个外角等于与它不相邻的两个内角的和,而不是任意两个内角之和,故结论②错误.
结论③:如图,△ABC为钝角三角形.
在△ABC中,三条高所在直线(即直线AD,BE,CF)的交点G在三角形外部,故结论③错误.
结论④:设∠A=(6x)°,根据∠A=2∠B=3∠C,则∠B=(3x)°,∠C=(2x)°.
在△ABC中,6x+3x+2x=11x=180,∴,
∴∠A,∠B,∠C均不等于90°.∴△ABC不是直角三角形.故结论④错误.
综上所述,正确的结论只有结论①.故本题应填写:①
.
18.
(1)如图所示:
(2)如图所示;
(3)S△BCD=20-5-1-10=4.
19.
证明:∵AB∥DC(已知)
∴∠1=∠CFE(两直线平行,同位角相等)
∵AE平分∠BAD(已知)
∴∠1=∠2(角平分线的定义)
∴∠CFE=∠2(等量代换)
∵∠CFE=∠E(已知)
∴∠2=∠E(等量代换)
∴AD∥BC(内错角相等,两直线平行).
20.
(1)证明:∵∠ABC=180°-∠A,
∴∠ABC+∠A=180°,
∴AD∥BC;
(2)∵AD∥BC,∠ADB=36°,
∴∠DBC=∠ADB=36°,
∵BD⊥CD,EF⊥CD,
∴BD∥EF,
∴∠DBC=∠EFC=36°
21.
∵GH⊥CD,
∴∠CHG=90°.
又∵∠2=30°,
∴∠3=60°.
∴∠4=60°.
又∵∠1=60°,
∴∠1=∠4.
∴AB∥CD(同位角相等,两直线平行).
22.
(1)∵在Rt△ABC中,∠ACB=90°,∠A=40°,
∴∠ABC=90°﹣∠A=50°,
∴∠CBD=130°.
∵BE是∠CBD的平分线,
∴∠CBE=∠CBD=65°;
(2)∵∠ACB=90°,∠CBE=65°,
∴∠CEB=90°﹣65°=25°.
∵DF∥BE,
∴∠F=∠CEB=25°.
23.
(1)∵在△ABC中,∠ABC=40°,∠ACB=80°,
∴∠BAC=180°-40°-80°=60°,
∵AE平分∠BAC,
∴∠BAE=30°;
(2)∵AD是△ABC的高,
∴∠ADB=90°,
∴∠BAD=180°-90°-40°=50°,
∴∠DAE=∠BAD-∠BAE=50°-30°=20°.
24.
解:(1)如图1,∵BC⊥AF于点C,
∴∠A+∠B=90°,
又∵∠A+∠1=90°,
∴∠B=∠1,
∴AB∥DE.
(2)如图2,当点P在A,D之间时,过P作PG∥AB,
∵AB∥DE,
∴PG∥DE,
∴∠ABP=∠GPB,∠DEP=∠GPE,
∴∠BPE=∠BPG+∠EPG=∠ABP+∠DEP;
如图所示,当点P在C,D之间时,过P作PG∥AB,
∵AB∥DE,
∴PG∥DE,
∴∠ABP=∠GPB,∠DEP=∠GPE,
∴∠BPE=∠BPG﹣∠EPG=∠ABP﹣∠DEP;
如图所示,当点P在C,F之间时,过P作PG∥AB,
∵AB∥DE,
∴PG∥DE,
∴∠ABP=∠GPB,∠DEP=∠GPE,
∴∠BPE=∠EPG﹣∠BPG=∠DEP﹣∠ABP.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
