人教版数学九年级下册导学案:27.2 相似三角形判定的常见类型
文档属性
| 名称 | 人教版数学九年级下册导学案:27.2 相似三角形判定的常见类型 |
|
|
| 格式 | zip | ||
| 文件大小 | 71.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 00:00:00 | ||
图片预览

文档简介
永昌三中
人教版八年级数学(下)第二十章学案
主备人:吴俊刚
审核人:苏建礼
班级:
姓名:
时间:2012.6.21
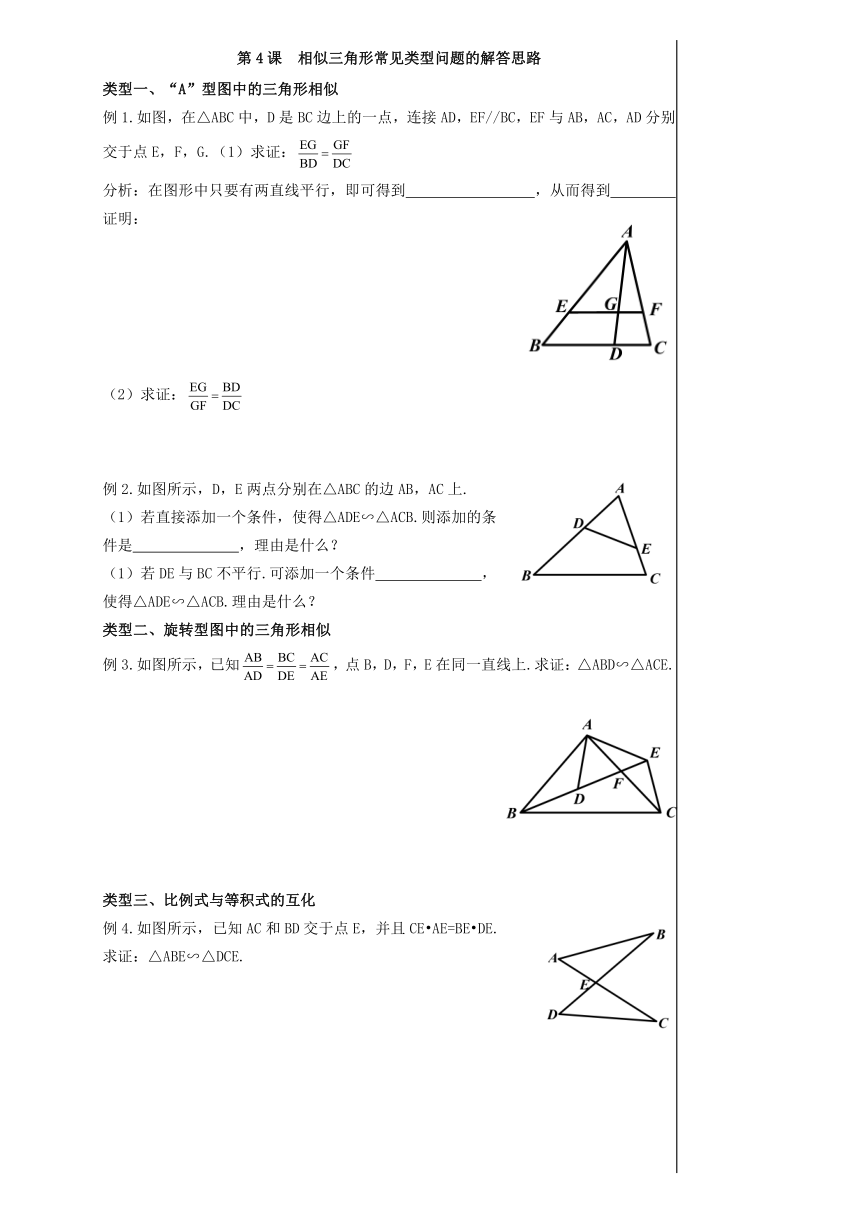
第4课
相似三角形常见类型问题的解答思路
类型一、“A”型图中的三角形相似
例1.如图,在△ABC中,D是BC边上的一点,连接AD,EF//BC,EF与AB,AC,AD分别交于点E,F,G.(1)求证:
分析:在图形中只要有两直线平行,即可得到
,从而得到
证明:
(2)求证:
例2.如图所示,D,E两点分别在△ABC的边AB,AC上.
(1)若直接添加一个条件,使得△ADE∽△ACB.则添加的条件是
,理由是什么?
(1)若DE与BC不平行.可添加一个条件
,使得△ADE∽△ACB.理由是什么?
类型二、旋转型图中的三角形相似
例3.如图所示,已知,点B,D,F,E在同一直线上.求证:△ABD∽△ACE.
类型三、比例式与等积式的互化
例4.如图所示,已知AC和BD交于点E,并且CE?AE=BE?DE.
求证:△ABE∽△DCE.
例5.如图,在梯形ABCD中,AD//BC,对角线AC,BD交于点O,BE//CD交CA的延长线于点E.求证:OC2=OA?OE
类型四、垂直型图形中的三角形相似
例6.如图,在Rt△ABC中,∠ACB=90°,CD⊥BD于点D.
(1)有这样几个结论:CD2=AD?BD;
AC2=AD?AB;
BC2=BD?AB.请判断它们是否正确.
(2)若正确,请选择其中一个进行证明.
类型五、存在特殊(特殊关系)的边或角的图形中三角形的相似
例7.如图,在Rt△ABC中,∠BAC=90°,AB=AC,E,D分别是BC,AC上的点,且∠AED=45°.
求证:△ABE∽△ECD.
人教版八年级数学(下)第二十章学案
主备人:吴俊刚
审核人:苏建礼
班级:
姓名:
时间:2012.6.21
第4课
相似三角形常见类型问题的解答思路
类型一、“A”型图中的三角形相似
例1.如图,在△ABC中,D是BC边上的一点,连接AD,EF//BC,EF与AB,AC,AD分别交于点E,F,G.(1)求证:
分析:在图形中只要有两直线平行,即可得到
,从而得到
证明:
(2)求证:
例2.如图所示,D,E两点分别在△ABC的边AB,AC上.
(1)若直接添加一个条件,使得△ADE∽△ACB.则添加的条件是
,理由是什么?
(1)若DE与BC不平行.可添加一个条件
,使得△ADE∽△ACB.理由是什么?
类型二、旋转型图中的三角形相似
例3.如图所示,已知,点B,D,F,E在同一直线上.求证:△ABD∽△ACE.
类型三、比例式与等积式的互化
例4.如图所示,已知AC和BD交于点E,并且CE?AE=BE?DE.
求证:△ABE∽△DCE.
例5.如图,在梯形ABCD中,AD//BC,对角线AC,BD交于点O,BE//CD交CA的延长线于点E.求证:OC2=OA?OE
类型四、垂直型图形中的三角形相似
例6.如图,在Rt△ABC中,∠ACB=90°,CD⊥BD于点D.
(1)有这样几个结论:CD2=AD?BD;
AC2=AD?AB;
BC2=BD?AB.请判断它们是否正确.
(2)若正确,请选择其中一个进行证明.
类型五、存在特殊(特殊关系)的边或角的图形中三角形的相似
例7.如图,在Rt△ABC中,∠BAC=90°,AB=AC,E,D分别是BC,AC上的点,且∠AED=45°.
求证:△ABE∽△ECD.
