北师大版数学八年级下册6.1.2 平行四边形的对角线性质 课件(19张)
文档属性
| 名称 | 北师大版数学八年级下册6.1.2 平行四边形的对角线性质 课件(19张) |  | |
| 格式 | pptx | ||
| 文件大小 | 352.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 16:26:16 | ||
图片预览






文档简介
第六章 平行四边形
1 平行四边形的性质
课时2 平行四边形的对角线性质
平行四边形的对角线互相平分
平行四边形的面积(重点、难点)
学习目标
新课导入
平行四边形的性质:
对边相等;
对角相等
新课讲解
知识点1 平行四边形对角线互相平分
在上一课的“做一做”中,我们还发现:平行
四边形的对角线互相平分. 请你尝试证明这一结论.
新课讲解
例
典例分析
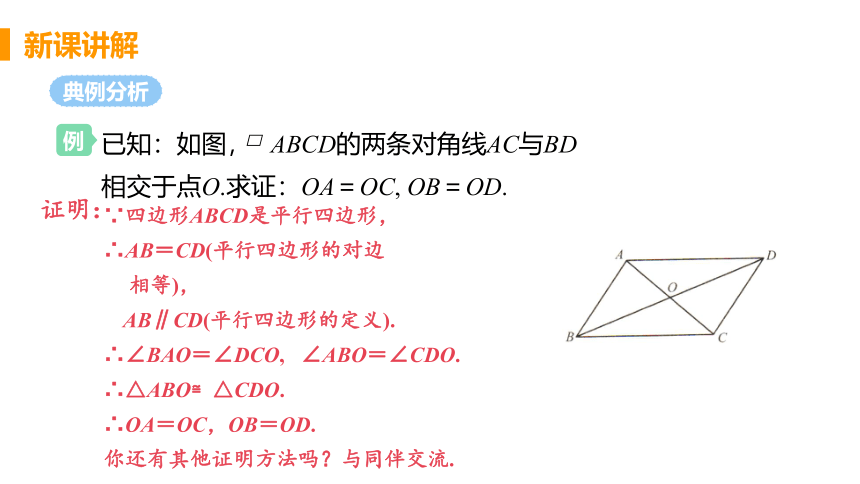
已知:如图, ABCD的两条对角线AC与BD相交于点O.求证:OA=OC, OB=OD.
∵四边形ABCD是平行四边形,
∴AB=CD(平行四边形的对边
相等),
AB∥CD(平行四边形的定义).
∴∠BAO=∠DCO, ∠ABO=∠CDO.
∴△ABO≌△CDO.
∴OA=OC,OB=OD.
你还有其他证明方法吗?与同伴交流.
证明:
新课讲解
对角线的性质:平行四边形的对角线互相平分.
数学表达式:
如图,∵四边形ABCD是平行四边形,
对角线AC,BD相交于点O,
∴OA=OC,OB=OD.
新课讲解
例
典例分析
证明:
∵四边形ABCD是平行四边形,
∴DO=BO(平行四边形的对角线互相平分),
AD∥BC(平行四边形的定义).
∴∠ODE=∠OBF.
∵∠DOE=∠BOF,
∴△DOE≌△BOF. ∴OE=OF.
已知:如图, ABCD的对角线AC与BD相交于点O,
过点O的直线与AD,BC分别相交于点E,F.
求证:OE=OF.
新课讲解
练一练
已知?ABCD的对角线AC与BD相交于点O,OA,OB,AB他的长分别为3,4,5,求其他各边以及两条对角线的长度.
因为平行四边形的对角线互相平分,
所以AC=2OA=6 ,BD=2OB=8 .
又因为OA2+OB2=32+42=52=AB2,所以AC⊥BD.
由勾股定理,可得AD2=OA2+OD2,
而OD=OB,所以AD2=32+42.
所以AD=5. 同理,可得DC=5,BC=5.
解:
新课讲解
知识点2 平行四边形的面积
1.面积公式:平行四边形的面积=底×高(底为平行四边形的任意一条边,高为这条边与其对边间的距离);
2.等底等高的平行四边形的面积相等.
新课讲解
例
典例分析
如图,在 ABCD中,DE平分∠ADC,AD=6,BE=2,则 ABCD的周长是________.
20
新课讲解
求 ABCD的周长,已知一条边AD=6,只需求出AD的邻边AB或CD的长即可.
∵四边形ABCD是平行四边形,AD=6,BE=2,
∴AD=BC=6,AD∥BC.
∴EC=BC-BE=6-2=4,∠ADE=∠DEC.
∵DE平分∠ADC,∴∠ADE=∠EDC.
∴∠EDC=∠DEC. ∴DC=EC=4.
∴ ABCD的周长是2×(4+6)=20.
分析:
新课讲解
例
典例分析
如图,在 ABCD中,AB=4,BC=6,
∠B=30°,则此平行四边形的面积是( )
A.6
B.12
C.18
D.24
B
新课讲解
过点A作AE⊥BC于E,根据含30°角的直角三角形
的性质:在直角三角形中,30°角所对的直角边等
于斜边的一半可求出AE的长,利用平行四边形的面
积公式即可求出其面积.
如图,过点A作AE⊥BC于E,
∵在直角三角形ABE中,
∠B=30°,
∴AE= ×AB= ×4=2.
∴平行四边形ABCD的面积=BC·AE=6×2=12.
分析:
新课讲解
练一练
如图,若?ABCD的周长为36 cm,过点D分别作AB,BC边上的高DE,DF,且DE=4 cm,DF=5 cm,?ABCD的面积为( )cm2.
A.40
B.32
C.36
D.50
A
课堂小结
1. 平行四边形的对角线互相平分.
2. 平行四边形的面积=底×高(底为平行四边形的任意一条边,高为这条边与其对边间的距离).
当堂小练
如图,在平行四边形ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则图中阴影部分的面积为( )
A.3
B.6
C.12
D.24
C
拓展与延伸
如图,在平行四边形ABCD中,AC和BD相交于点O,OE⊥AD于点E,OF⊥BC于点F.
试说明:OE=OF.
拓展与延伸
∵四边形ABCD为平行四边形,
∴AD∥BC,OA=OC,
∴∠EAO=∠FCO,
∵OE⊥AD,OF⊥BC,
∴∠AEO=∠CFO=90°,
∴△AOE≌△COF,
∴OE=OF.
解:
布置作业
请完成对应习题
1 平行四边形的性质
课时2 平行四边形的对角线性质
平行四边形的对角线互相平分
平行四边形的面积(重点、难点)
学习目标
新课导入
平行四边形的性质:
对边相等;
对角相等
新课讲解
知识点1 平行四边形对角线互相平分
在上一课的“做一做”中,我们还发现:平行
四边形的对角线互相平分. 请你尝试证明这一结论.
新课讲解
例
典例分析
已知:如图, ABCD的两条对角线AC与BD相交于点O.求证:OA=OC, OB=OD.
∵四边形ABCD是平行四边形,
∴AB=CD(平行四边形的对边
相等),
AB∥CD(平行四边形的定义).
∴∠BAO=∠DCO, ∠ABO=∠CDO.
∴△ABO≌△CDO.
∴OA=OC,OB=OD.
你还有其他证明方法吗?与同伴交流.
证明:
新课讲解
对角线的性质:平行四边形的对角线互相平分.
数学表达式:
如图,∵四边形ABCD是平行四边形,
对角线AC,BD相交于点O,
∴OA=OC,OB=OD.
新课讲解
例
典例分析
证明:
∵四边形ABCD是平行四边形,
∴DO=BO(平行四边形的对角线互相平分),
AD∥BC(平行四边形的定义).
∴∠ODE=∠OBF.
∵∠DOE=∠BOF,
∴△DOE≌△BOF. ∴OE=OF.
已知:如图, ABCD的对角线AC与BD相交于点O,
过点O的直线与AD,BC分别相交于点E,F.
求证:OE=OF.
新课讲解
练一练
已知?ABCD的对角线AC与BD相交于点O,OA,OB,AB他的长分别为3,4,5,求其他各边以及两条对角线的长度.
因为平行四边形的对角线互相平分,
所以AC=2OA=6 ,BD=2OB=8 .
又因为OA2+OB2=32+42=52=AB2,所以AC⊥BD.
由勾股定理,可得AD2=OA2+OD2,
而OD=OB,所以AD2=32+42.
所以AD=5. 同理,可得DC=5,BC=5.
解:
新课讲解
知识点2 平行四边形的面积
1.面积公式:平行四边形的面积=底×高(底为平行四边形的任意一条边,高为这条边与其对边间的距离);
2.等底等高的平行四边形的面积相等.
新课讲解
例
典例分析
如图,在 ABCD中,DE平分∠ADC,AD=6,BE=2,则 ABCD的周长是________.
20
新课讲解
求 ABCD的周长,已知一条边AD=6,只需求出AD的邻边AB或CD的长即可.
∵四边形ABCD是平行四边形,AD=6,BE=2,
∴AD=BC=6,AD∥BC.
∴EC=BC-BE=6-2=4,∠ADE=∠DEC.
∵DE平分∠ADC,∴∠ADE=∠EDC.
∴∠EDC=∠DEC. ∴DC=EC=4.
∴ ABCD的周长是2×(4+6)=20.
分析:
新课讲解
例
典例分析
如图,在 ABCD中,AB=4,BC=6,
∠B=30°,则此平行四边形的面积是( )
A.6
B.12
C.18
D.24
B
新课讲解
过点A作AE⊥BC于E,根据含30°角的直角三角形
的性质:在直角三角形中,30°角所对的直角边等
于斜边的一半可求出AE的长,利用平行四边形的面
积公式即可求出其面积.
如图,过点A作AE⊥BC于E,
∵在直角三角形ABE中,
∠B=30°,
∴AE= ×AB= ×4=2.
∴平行四边形ABCD的面积=BC·AE=6×2=12.
分析:
新课讲解
练一练
如图,若?ABCD的周长为36 cm,过点D分别作AB,BC边上的高DE,DF,且DE=4 cm,DF=5 cm,?ABCD的面积为( )cm2.
A.40
B.32
C.36
D.50
A
课堂小结
1. 平行四边形的对角线互相平分.
2. 平行四边形的面积=底×高(底为平行四边形的任意一条边,高为这条边与其对边间的距离).
当堂小练
如图,在平行四边形ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则图中阴影部分的面积为( )
A.3
B.6
C.12
D.24
C
拓展与延伸
如图,在平行四边形ABCD中,AC和BD相交于点O,OE⊥AD于点E,OF⊥BC于点F.
试说明:OE=OF.
拓展与延伸
∵四边形ABCD为平行四边形,
∴AD∥BC,OA=OC,
∴∠EAO=∠FCO,
∵OE⊥AD,OF⊥BC,
∴∠AEO=∠CFO=90°,
∴△AOE≌△COF,
∴OE=OF.
解:
布置作业
请完成对应习题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
