北师大版数学八年级下册6.2.1 由边的关系判定平行四边形 课件(19张)
文档属性
| 名称 | 北师大版数学八年级下册6.2.1 由边的关系判定平行四边形 课件(19张) |  | |
| 格式 | pptx | ||
| 文件大小 | 545.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 16:26:42 | ||
图片预览





文档简介
第六章 平行四边形
2 平行四边形的判定
课时1 由边的关系判定平行四边形
由两组对边关系判定平行四边形
由一组对边的关系判定平行四边形(重点、难点)
学习目标
新课导入
平行四边形的性质
平行四边形对边平行;
平行四边形对边相等;
平行四边形对角相等;
平行四边形对角线互相平分;
新课讲解
知识点1 由两组对边关系判定平行四边形
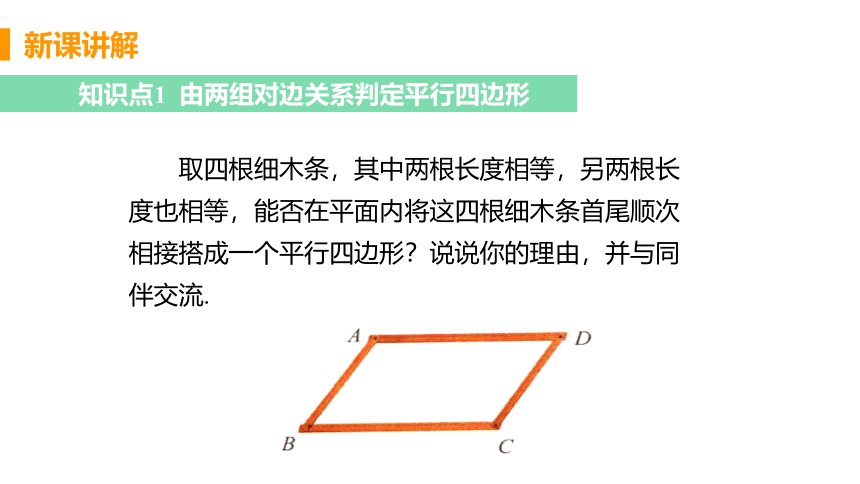
取四根细木条,其中两根长度相等,另两根长
度也相等,能否在平面内将这四根细木条首尾顺次
相接搭成一个平行四边形?说说你的理由,并与同
伴交流.
新课讲解
例
典例分析
已知:如图(1),在四边形ABCD中,AB=CD,AD=CB
求证:四边形ABCD是平行四边形.
如图 (2),连接BD.
在△ABD和△CDB中,
∵AB=CD, AD=CB, BD=DB,
∴△ABD≌△CDB.
∴∠1=∠2, ∠3=∠4.
∴AB∥CD, AD∥CB.
∴四边形ABCD是平行四边形
(平行四边形的定义).
证明:
新课讲解
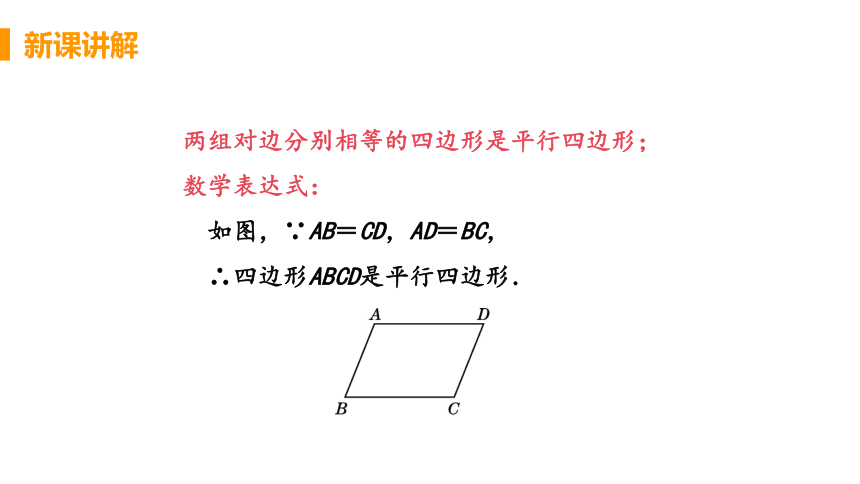
两组对边分别相等的四边形是平行四边形;
数学表达式:
如图,∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
新课讲解
例
典例分析
如图,已知四边形ABCD是平行四边形,DE平分∠ADC,交CB的延长线于点E,BF平分∠ABC,交AD的延长线于点F.
求证:四边形BFDE是平行四边形.
要证四边形BFDE是平行四
边形,根据平行四边形的定
义可证得DF∥BE,因此可
采用判定方法一即定义法,
只需证明DE∥FB即可.
分析:
新课讲解
∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,AD∥CB. ∴DF∥BE.
∵DE平分∠ADC,BF平分∠ABC,
∴∠1=∠2=∠3=∠4.
∵AD∥BC,∴∠1=∠E. ∴∠E=∠3.
∴DE∥FB.
∴四边形BFDE是平行四边形(两组对边分别平
行的四边形是平行四边形).
证明:
新课讲解
练一练
四边形的四条边长分别是a,b,c,d,其中a,b为
一组对边长,c,d为另一组对边长且a2+b2+c2+d2
=2ab+2cd,则这个四边形是( )
A.任意四边形
B.平行四边形
C.对角线相等的四边形
D.对角线垂直的四边形
B
新课讲解
知识点2 由一组对边的关系判定平行四边形
(1)取两根长度相等的细木条,你能将它们摆放在一
张纸上,使得这两根细木条的四个端点恰好是一
个平行四边形的四个顶点吗?
(2)如果四边形有一组对边相等,那么还需要添加什
么条件,才能使它成为平行四边形?与同伴交流.
新课讲解
例
典例分析
如图 (2),连接AC.
∵AB∥CD,∴∠BAC=∠DCA.
又∵AB=CD,AC=CA,
∴△ABC≌△CDA.
∴BC=DA.
∴四边形ABCD是平行四边形(两组对边分别相
等的四边形是平行 四边形).
已知:如图(1),在四边形ABCD中,AB CD.
求证:四边形ABCD是平行四边形.
证明:
新课讲解
一组对边平行且相等的四边形是平行四边形;
数学表达式:
如图,∵AB CD,
∴四边形ABCD是平行四边形.
新课讲解
例
典例分析
已知:如图,在 ABCD中,E, F分别为AD和CB的中点.
求证:四边形BFDE是平行四边形.
∵四边形ABCD是平行四边形,
∴AD=CB(平行四边形的对边相等),
AD∥CB(平行四边形的定义).
∵E,F分别是AD和CB的中点,
∴ED=FB,ED∥FB.
∴四边形DFDE是平行四边形(一组对边平行且
相等的四边形是平行四边形).
证明:
新课讲解
练一练
如图,线段AD是线段BC经过平移得到的,分别连接AB,CD,四边形ABCD是平行四边形吗?请说明理由
四边形ABCD是平行四边形.
理由:由平移的性质可知BC,AD是四边形ABCD的一组平行且相等的对边.
解:
课堂小结
有边判定四边形是平行四边形的方法有:
1.定义:两组对边分别平行的四边形是平行四边形.
2.两组对边分别相等的四边形是平行四边形.
3.一组对边平行且相等的四边形是平行四边形.
当堂小练
在四边形ABCD中,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD中任选两个使四边形ABCD为平行四边形的选法有( )
A.3种 B.4种
C.5种 D.6种
B
当堂小练
如图,在四边形ABCD中,AB∥CD,要使四边形ABCD是平行四边形,可添加的条件不正确的是( )
A.AB=CD
B.BC=AD
C.∠A=∠C
D.BC∥AD
B
拓展与延伸
判断符合下列条件的四边形ABCD是否是平行四边形.
(1)AB∥CD,∠A=∠C;
(2)AB∥CD,BC=AD.
(1)是.∵AB∥CD,
∴∠A+∠D=180°.
又∵∠A=∠C,
∴∠C+∠D=180°.
∴AD∥BC.
∴四边形ABCD为平行四边形.
(2)不是.反例:如图.
该四边形是等腰梯形,而不是平行四边形.
布置作业
请完成对应习题
2 平行四边形的判定
课时1 由边的关系判定平行四边形
由两组对边关系判定平行四边形
由一组对边的关系判定平行四边形(重点、难点)
学习目标
新课导入
平行四边形的性质
平行四边形对边平行;
平行四边形对边相等;
平行四边形对角相等;
平行四边形对角线互相平分;
新课讲解
知识点1 由两组对边关系判定平行四边形
取四根细木条,其中两根长度相等,另两根长
度也相等,能否在平面内将这四根细木条首尾顺次
相接搭成一个平行四边形?说说你的理由,并与同
伴交流.
新课讲解
例
典例分析
已知:如图(1),在四边形ABCD中,AB=CD,AD=CB
求证:四边形ABCD是平行四边形.
如图 (2),连接BD.
在△ABD和△CDB中,
∵AB=CD, AD=CB, BD=DB,
∴△ABD≌△CDB.
∴∠1=∠2, ∠3=∠4.
∴AB∥CD, AD∥CB.
∴四边形ABCD是平行四边形
(平行四边形的定义).
证明:
新课讲解
两组对边分别相等的四边形是平行四边形;
数学表达式:
如图,∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
新课讲解
例
典例分析
如图,已知四边形ABCD是平行四边形,DE平分∠ADC,交CB的延长线于点E,BF平分∠ABC,交AD的延长线于点F.
求证:四边形BFDE是平行四边形.
要证四边形BFDE是平行四
边形,根据平行四边形的定
义可证得DF∥BE,因此可
采用判定方法一即定义法,
只需证明DE∥FB即可.
分析:
新课讲解
∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,AD∥CB. ∴DF∥BE.
∵DE平分∠ADC,BF平分∠ABC,
∴∠1=∠2=∠3=∠4.
∵AD∥BC,∴∠1=∠E. ∴∠E=∠3.
∴DE∥FB.
∴四边形BFDE是平行四边形(两组对边分别平
行的四边形是平行四边形).
证明:
新课讲解
练一练
四边形的四条边长分别是a,b,c,d,其中a,b为
一组对边长,c,d为另一组对边长且a2+b2+c2+d2
=2ab+2cd,则这个四边形是( )
A.任意四边形
B.平行四边形
C.对角线相等的四边形
D.对角线垂直的四边形
B
新课讲解
知识点2 由一组对边的关系判定平行四边形
(1)取两根长度相等的细木条,你能将它们摆放在一
张纸上,使得这两根细木条的四个端点恰好是一
个平行四边形的四个顶点吗?
(2)如果四边形有一组对边相等,那么还需要添加什
么条件,才能使它成为平行四边形?与同伴交流.
新课讲解
例
典例分析
如图 (2),连接AC.
∵AB∥CD,∴∠BAC=∠DCA.
又∵AB=CD,AC=CA,
∴△ABC≌△CDA.
∴BC=DA.
∴四边形ABCD是平行四边形(两组对边分别相
等的四边形是平行 四边形).
已知:如图(1),在四边形ABCD中,AB CD.
求证:四边形ABCD是平行四边形.
证明:
新课讲解
一组对边平行且相等的四边形是平行四边形;
数学表达式:
如图,∵AB CD,
∴四边形ABCD是平行四边形.
新课讲解
例
典例分析
已知:如图,在 ABCD中,E, F分别为AD和CB的中点.
求证:四边形BFDE是平行四边形.
∵四边形ABCD是平行四边形,
∴AD=CB(平行四边形的对边相等),
AD∥CB(平行四边形的定义).
∵E,F分别是AD和CB的中点,
∴ED=FB,ED∥FB.
∴四边形DFDE是平行四边形(一组对边平行且
相等的四边形是平行四边形).
证明:
新课讲解
练一练
如图,线段AD是线段BC经过平移得到的,分别连接AB,CD,四边形ABCD是平行四边形吗?请说明理由
四边形ABCD是平行四边形.
理由:由平移的性质可知BC,AD是四边形ABCD的一组平行且相等的对边.
解:
课堂小结
有边判定四边形是平行四边形的方法有:
1.定义:两组对边分别平行的四边形是平行四边形.
2.两组对边分别相等的四边形是平行四边形.
3.一组对边平行且相等的四边形是平行四边形.
当堂小练
在四边形ABCD中,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD中任选两个使四边形ABCD为平行四边形的选法有( )
A.3种 B.4种
C.5种 D.6种
B
当堂小练
如图,在四边形ABCD中,AB∥CD,要使四边形ABCD是平行四边形,可添加的条件不正确的是( )
A.AB=CD
B.BC=AD
C.∠A=∠C
D.BC∥AD
B
拓展与延伸
判断符合下列条件的四边形ABCD是否是平行四边形.
(1)AB∥CD,∠A=∠C;
(2)AB∥CD,BC=AD.
(1)是.∵AB∥CD,
∴∠A+∠D=180°.
又∵∠A=∠C,
∴∠C+∠D=180°.
∴AD∥BC.
∴四边形ABCD为平行四边形.
(2)不是.反例:如图.
该四边形是等腰梯形,而不是平行四边形.
布置作业
请完成对应习题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
