北师大版数学八年级下册6.2.2 由对角线的关系判定平行四边形 课件(22张)
文档属性
| 名称 | 北师大版数学八年级下册6.2.2 由对角线的关系判定平行四边形 课件(22张) |  | |
| 格式 | pptx | ||
| 文件大小 | 593.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 16:26:46 | ||
图片预览






文档简介
第六章 平行四边形
2 平行四边形的判定
课时2 由对角线的关系判定平行四边形
判定平行四边形
由对角线的关系判定平行四边形
平行四边形判定方法的综合应用(重点、难点)
学习目标
新课导入
平行四边形的判定方法有哪些?
新课讲解
知识点1 由对角线的关系判定平行四边形
前面我们已经得到了平行四边形的两个判定方法,你还
能找到其他的判定方法吗?
你同意他的想法吗?你能证明他的猜想吗?请你试一试.
如图,将两根木条AC,BD
的中点重叠,并用钉子固定,
四边形ABCD看起来是平行四
边形. 于是我猜想:对角线互
相平分的四边形是平行四边形.
新课讲解
例
典例分析
已知:如图,四边形ABCD的两条对角线AC与BD相交于点O, 并且OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
∵OA=OC,OD=OB,
∠AOD=∠COB.
∴△AOD≌△COB.
∴AD=CB,∠ADO=∠CBO.
∴AD∥CB.
∴四边形ABCD是平行四边形(一组对边平行且相
等的四边形是平行 四边形).
证明:
新课讲解
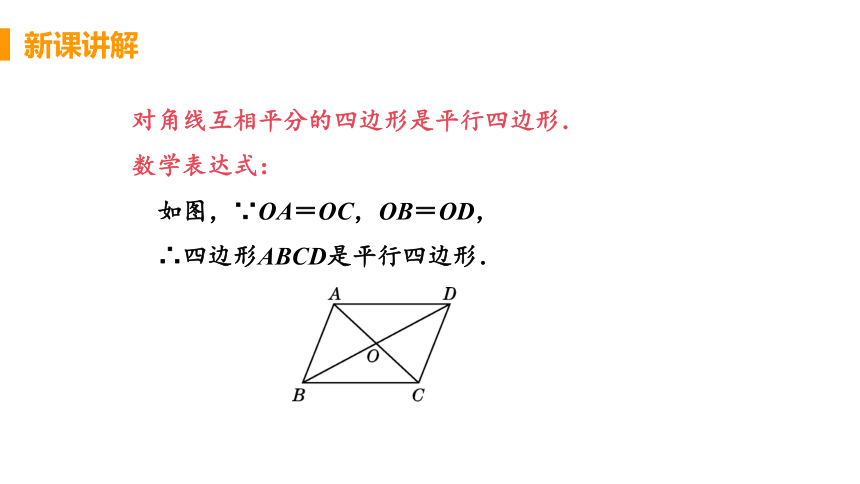
对角线互相平分的四边形是平行四边形.
数学表达式:
如图,∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形.
新课讲解
例
典例分析
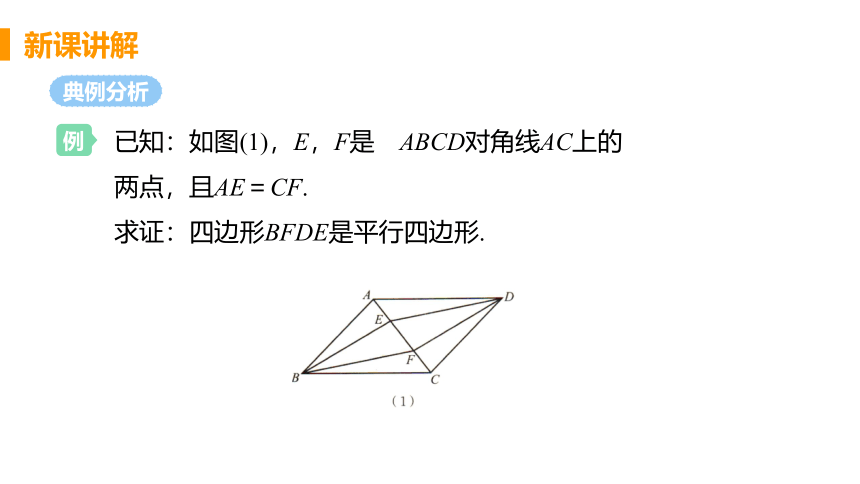
已知:如图(1),E,F是 ABCD对角线AC上的
两点,且AE=CF.
求证:四边形BFDE是平行四边形.
新课讲解
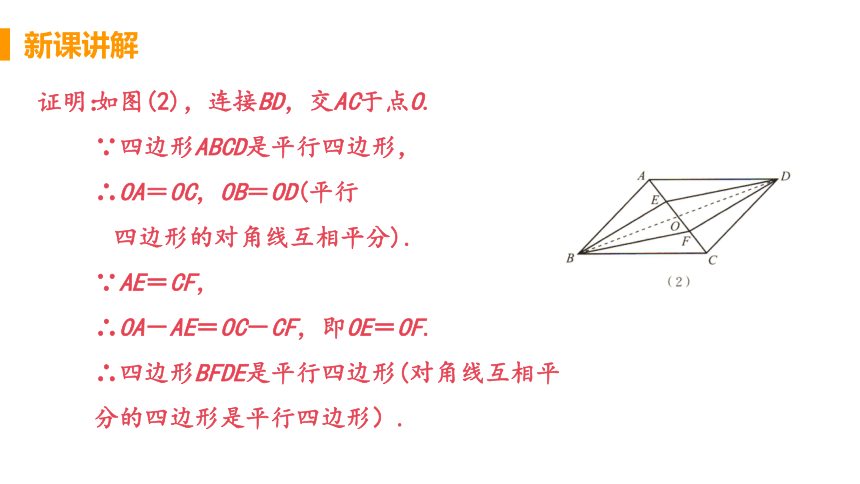
证明:
如图(2),连接BD,交AC于点O.
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD(平行
四边形的对角线互相平分).
∵AE=CF,
∴OA-AE=OC-CF,即OE=OF.
∴四边形BFDE是平行四边形(对角线互相平分的四边形是平行四边形).
新课讲解
练一练
如图,在 ABCD中,对角线AC与BD相交于点O,点E,F分别是OA和OC的 中点,四边形BFDE是平行四边形吗?
请说明理由.
四边形BFDE是平行四边形,
理由:∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC.
又∵E,F分别是OA和OC的中点,
∴OE=OF. ∴四边形BFDE是平行四边形.
解:
B
C
D
新课讲解
知识点2 平行四边形判定方法的综合应用
平行四边形的判定方法:
(1)定义:两组对边分别平行的四边形是平行四边形.
(2)两组对边分别相等的四边形是平行四边形.
(3)一组对边平行且相等的四边形是平行四边形.
(4)两组对角分别相等的四边形是平行四边形.
(5)对角线互相平分的四边形是平行四边形.
新课讲解
例
典例分析
如图,四边形ABCD是平行四边形,E,F为对角线AC上两点,连接ED,EB,FD,FB.给出以下结论:①BE∥DF;②BE=DF;③AE=CF.请你从中选取一个条件,使∠1=∠2成立,并给出证明.
分析:
欲证明∠1=∠2,只需证得
四边形EDFB是平行四边形
或△ABF≌△CDE即可.
新课讲解
(1)补充条件①BE∥DF.
证明:∵BE∥DF,
∴∠BEC=∠DFA. ∴∠BEA=∠DFC.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD. ∴∠BAE=∠DCF.
在△ABE与△CDF中,
∴△ABE≌△CDF(AAS).
∴BE=DF. ∴四边形BFDE是平行四边形.
∴ED∥BF. ∴∠1=∠2.
解:
新课讲解
(2)补充条件③AE=CF.
证明:∵AE=CF,∴AF=CE.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∴∠BAF=∠DCE.
在△ABF与△CDE中,
∴△ABF≌△CDE(SAS).
∴∠1=∠2.
新课讲解
练一练
如图,在 ABCD中,∠ABC=70°,∠ABC的平分线交AD于点E,过点D作BE的平行线交BC于点F,求∠CDF的度数.
A
E
D
新课讲解
∵四边形ABCD是平行四边形,
∴AD∥BC,∠ABC=∠ADC.
∴ED∥BF. 又∵BE∥DF,
∴四边形BEDF是平行四边形.
∴∠EBF=∠FDE.
∵∠ABC=70°,BE平分∠ABC,
∴∠EBF= ∠ABC=35°.∴∠FDE=35°.
∵∠ABC=∠ADC,
∴∠CDF=∠ADC-∠FDE=35°.
解:
课堂小结
平行四边形的判定方法:
(1)定义:两组对边分别平行的四边形是平行四边形.
(2)两组对边分别相等的四边形是平行四边形.
(3)对角线互相平分的四边形是平行四边形.
(4)两组对角分别相等的四边形是平行四边形.
(5)一组对边平行且相等的四边形是平行四边形.
当堂小练
下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形
D
当堂小练
如图,四边形ABCD的对角线相交于点O,AO=CO,请添加一个条件_______________________(只添一个即可),使四边形ABCD是平行四边形.
BO=DO(答案不唯一)
拓展与延伸
如图,在?ABCD中,对角线AC,BD相交于O,E,F是对角线AC上的两点,给出下列4个条件:①OE=OF;②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF.其中不能判定四边形DEBF是平行四边形的有( )
A.0个 B.1个
C.2个 D.3个
B
拓展与延伸
给出条件①OE=OF,
由四边形ABCD是平行四边形,可得OD=OB.
又∵OE=OF,∴四边形DEBF为平行四边形.
故③正确.故①正确.故③正确.
给出条件③∠ADE=∠CBF,
∵四边形ABCD是平行四边形,
∴AD=CB,AD∥CB.∴∠DAE=∠BCF.
又∵∠ADE=∠CBF,∴△ADE≌△CBF.
∴DE=BF,∠AED=∠CFB.
拓展与延伸
∴∠DEO=∠BFO.∴DE∥BF.
∴四边形DEBF为平行四边形.故③正确.
给出条件④∠ABE=∠CDF,理由同③,亦可判定四边形DEBF为平行四边形.故④正确.只有给出条件②无法判定四边形DEBF为平行四边形.故选B.本题易错选A.将DE=BF作为条件判定三角形全等,从而推出四边形DEBF为平行四边形.
布置作业
请完成对应习题
2 平行四边形的判定
课时2 由对角线的关系判定平行四边形
判定平行四边形
由对角线的关系判定平行四边形
平行四边形判定方法的综合应用(重点、难点)
学习目标
新课导入
平行四边形的判定方法有哪些?
新课讲解
知识点1 由对角线的关系判定平行四边形
前面我们已经得到了平行四边形的两个判定方法,你还
能找到其他的判定方法吗?
你同意他的想法吗?你能证明他的猜想吗?请你试一试.
如图,将两根木条AC,BD
的中点重叠,并用钉子固定,
四边形ABCD看起来是平行四
边形. 于是我猜想:对角线互
相平分的四边形是平行四边形.
新课讲解
例
典例分析
已知:如图,四边形ABCD的两条对角线AC与BD相交于点O, 并且OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
∵OA=OC,OD=OB,
∠AOD=∠COB.
∴△AOD≌△COB.
∴AD=CB,∠ADO=∠CBO.
∴AD∥CB.
∴四边形ABCD是平行四边形(一组对边平行且相
等的四边形是平行 四边形).
证明:
新课讲解
对角线互相平分的四边形是平行四边形.
数学表达式:
如图,∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形.
新课讲解
例
典例分析
已知:如图(1),E,F是 ABCD对角线AC上的
两点,且AE=CF.
求证:四边形BFDE是平行四边形.
新课讲解
证明:
如图(2),连接BD,交AC于点O.
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD(平行
四边形的对角线互相平分).
∵AE=CF,
∴OA-AE=OC-CF,即OE=OF.
∴四边形BFDE是平行四边形(对角线互相平分的四边形是平行四边形).
新课讲解
练一练
如图,在 ABCD中,对角线AC与BD相交于点O,点E,F分别是OA和OC的 中点,四边形BFDE是平行四边形吗?
请说明理由.
四边形BFDE是平行四边形,
理由:∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC.
又∵E,F分别是OA和OC的中点,
∴OE=OF. ∴四边形BFDE是平行四边形.
解:
B
C
D
新课讲解
知识点2 平行四边形判定方法的综合应用
平行四边形的判定方法:
(1)定义:两组对边分别平行的四边形是平行四边形.
(2)两组对边分别相等的四边形是平行四边形.
(3)一组对边平行且相等的四边形是平行四边形.
(4)两组对角分别相等的四边形是平行四边形.
(5)对角线互相平分的四边形是平行四边形.
新课讲解
例
典例分析
如图,四边形ABCD是平行四边形,E,F为对角线AC上两点,连接ED,EB,FD,FB.给出以下结论:①BE∥DF;②BE=DF;③AE=CF.请你从中选取一个条件,使∠1=∠2成立,并给出证明.
分析:
欲证明∠1=∠2,只需证得
四边形EDFB是平行四边形
或△ABF≌△CDE即可.
新课讲解
(1)补充条件①BE∥DF.
证明:∵BE∥DF,
∴∠BEC=∠DFA. ∴∠BEA=∠DFC.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD. ∴∠BAE=∠DCF.
在△ABE与△CDF中,
∴△ABE≌△CDF(AAS).
∴BE=DF. ∴四边形BFDE是平行四边形.
∴ED∥BF. ∴∠1=∠2.
解:
新课讲解
(2)补充条件③AE=CF.
证明:∵AE=CF,∴AF=CE.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∴∠BAF=∠DCE.
在△ABF与△CDE中,
∴△ABF≌△CDE(SAS).
∴∠1=∠2.
新课讲解
练一练
如图,在 ABCD中,∠ABC=70°,∠ABC的平分线交AD于点E,过点D作BE的平行线交BC于点F,求∠CDF的度数.
A
E
D
新课讲解
∵四边形ABCD是平行四边形,
∴AD∥BC,∠ABC=∠ADC.
∴ED∥BF. 又∵BE∥DF,
∴四边形BEDF是平行四边形.
∴∠EBF=∠FDE.
∵∠ABC=70°,BE平分∠ABC,
∴∠EBF= ∠ABC=35°.∴∠FDE=35°.
∵∠ABC=∠ADC,
∴∠CDF=∠ADC-∠FDE=35°.
解:
课堂小结
平行四边形的判定方法:
(1)定义:两组对边分别平行的四边形是平行四边形.
(2)两组对边分别相等的四边形是平行四边形.
(3)对角线互相平分的四边形是平行四边形.
(4)两组对角分别相等的四边形是平行四边形.
(5)一组对边平行且相等的四边形是平行四边形.
当堂小练
下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形
D
当堂小练
如图,四边形ABCD的对角线相交于点O,AO=CO,请添加一个条件_______________________(只添一个即可),使四边形ABCD是平行四边形.
BO=DO(答案不唯一)
拓展与延伸
如图,在?ABCD中,对角线AC,BD相交于O,E,F是对角线AC上的两点,给出下列4个条件:①OE=OF;②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF.其中不能判定四边形DEBF是平行四边形的有( )
A.0个 B.1个
C.2个 D.3个
B
拓展与延伸
给出条件①OE=OF,
由四边形ABCD是平行四边形,可得OD=OB.
又∵OE=OF,∴四边形DEBF为平行四边形.
故③正确.故①正确.故③正确.
给出条件③∠ADE=∠CBF,
∵四边形ABCD是平行四边形,
∴AD=CB,AD∥CB.∴∠DAE=∠BCF.
又∵∠ADE=∠CBF,∴△ADE≌△CBF.
∴DE=BF,∠AED=∠CFB.
拓展与延伸
∴∠DEO=∠BFO.∴DE∥BF.
∴四边形DEBF为平行四边形.故③正确.
给出条件④∠ABE=∠CDF,理由同③,亦可判定四边形DEBF为平行四边形.故④正确.只有给出条件②无法判定四边形DEBF为平行四边形.故选B.本题易错选A.将DE=BF作为条件判定三角形全等,从而推出四边形DEBF为平行四边形.
布置作业
请完成对应习题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
