11.2.1三角形全等的判定(sss)
文档属性
| 名称 | 11.2.1三角形全等的判定(sss) |

|
|
| 格式 | rar | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-07 00:00:00 | ||
图片预览


文档简介
(共14张PPT)
§13.2 三角形全等的条件(一)
教师 鲁玲
我们是最棒的!Come on!
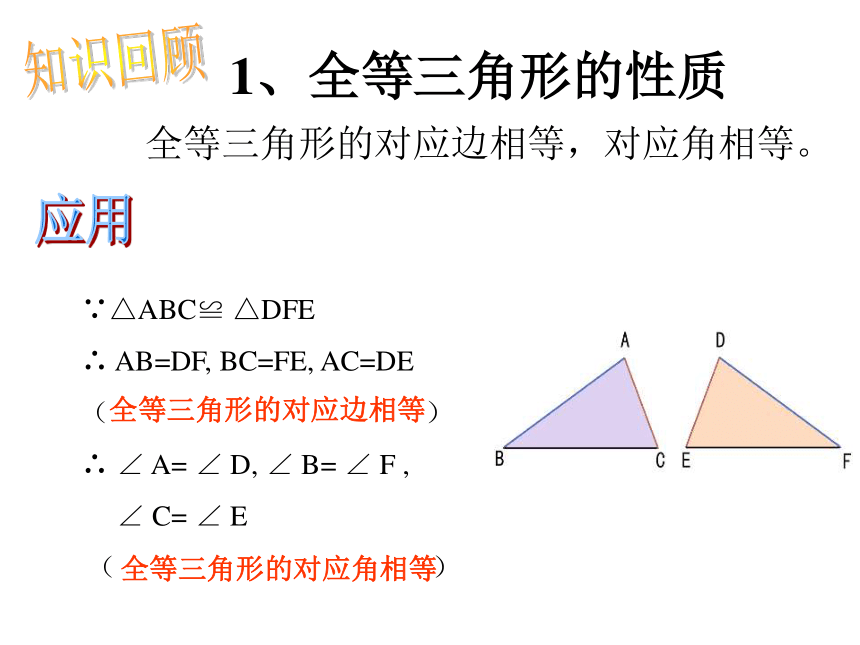
全等三角形的对应边相等,对应角相等。
∵△ABC≌ △DFE
∴ AB=DF, BC=FE, AC=DE
( )
∴ ∠ A= ∠ D, ∠ B= ∠ F ,
∠ C= ∠ E
( )
1、全等三角形的性质
全等三角形的对应边相等
全等三角形的对应角相等
2、三角形全等应具备什么条件?
“边边边”
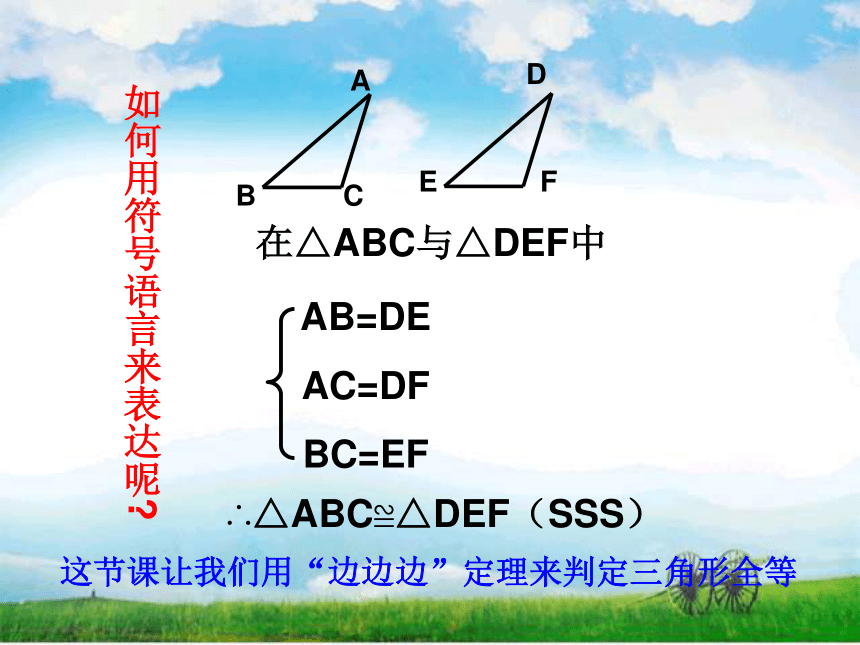
如何用符号语言来表达呢
在△ABC与△DEF中
A
B
C
D
E
F
AB=DE
AC=DF
BC=EF
∴△ABC≌△DEF(SSS)
这节课让我们用“边边边”定理来判定三角形全等
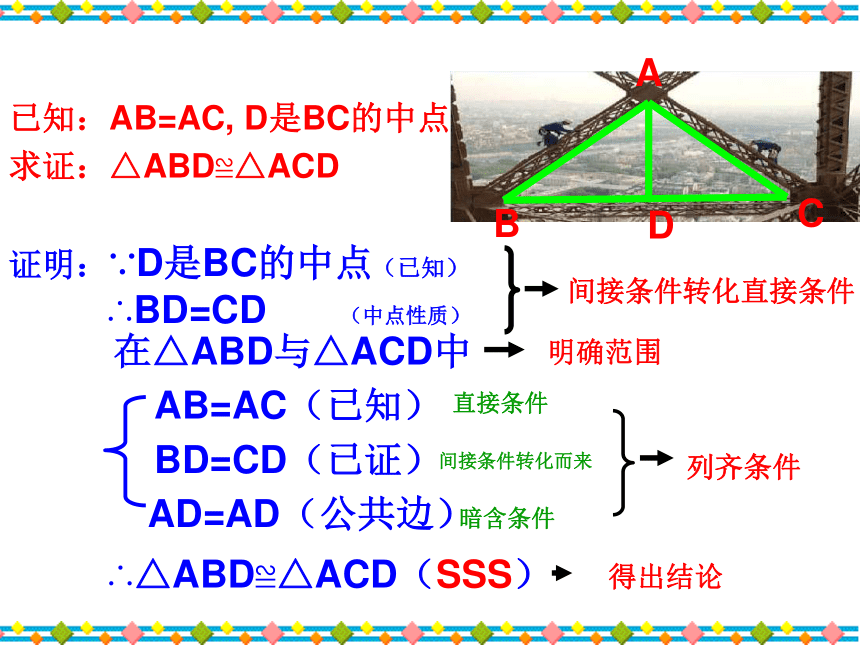
证明:∵D是BC的中点(已知)
∴BD=CD (中点性质)
在△ABD与△ACD中
AB=AC(已知)
BD=CD(已证)
AD=AD(公共边)
∴△ABD≌△ACD(SSS)
已知:AB=AC, D是BC的中点
求证:△ABD≌△ACD
A
B
C
D
间接条件转化直接条件
明确范围
列齐条件
得出结论
直接条件
间接条件转化而来
暗含条件
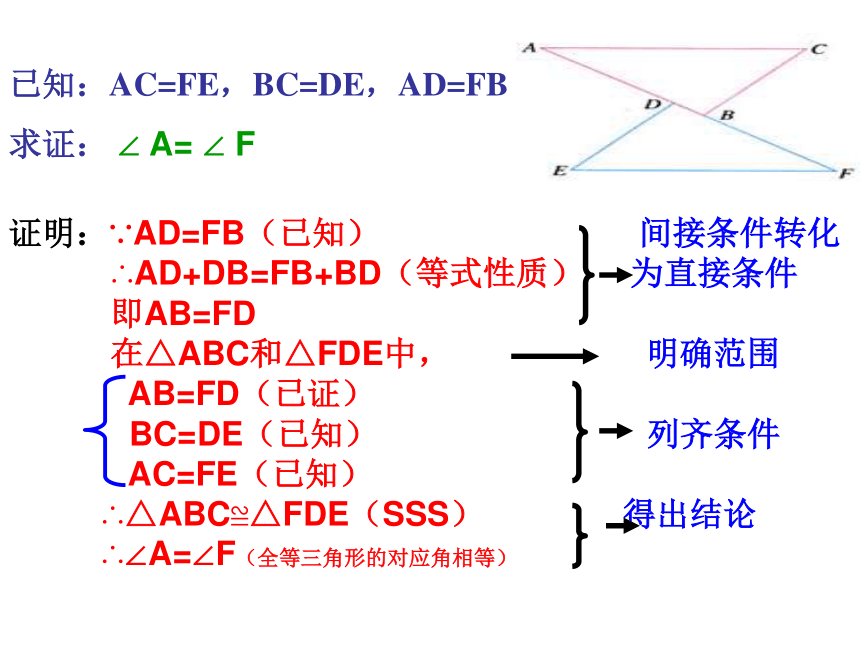
已知:AC=FE,BC=DE,AD=FB
求证: ∠ A= ∠ F
证明:∵AD=FB(已知) 间接条件转化
∴AD+DB=FB+BD(等式性质) 为直接条件
即AB=FD
在△ABC和△FDE中, 明确范围
AB=FD(已证)
BC=DE(已知) 列齐条件
AC=FE(已知)
∴△ABC≌△FDE(SSS) 得出结论
∴∠A=∠F(全等三角形的对应角相等)
A
D
B E F C
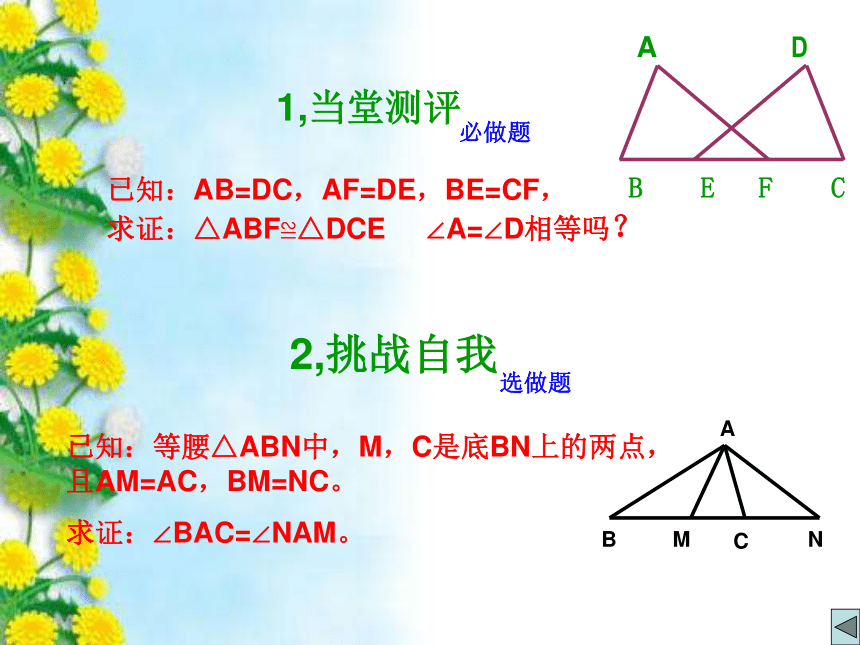
已知:AB=DC,AF=DE,BE=CF,
求证:△ABF≌△DCE ∠A=∠D相等吗?
1,当堂测评
A
B
M
C
N
已知:等腰△ABN中,M,C是底BN上的两点, 且AM=AC,BM=NC。
求证:∠BAC=∠NAM。
选做题
2,挑战自我
必做题
A
D
B E F C
证明:∵BE=CF(已知) (5分+5分)
∴BE+EF=CF+FE(等式性质) ( 5分+5分)
即BF=CE ( 10分)
在△ABF与△DCE中, ( 10分)
AB=DC(已知) ( 5分+5分)
(10分) BF=CE(已证) ( 5分+5分)
AF=DE(已知) ( 5分+5分)
∴△ABF≌△DCE(SSS) ( 5分+5分)
∴∠A=∠D(全等三角形的对应角相等) ( 5分+5分)
已知:AB=DC,AF=DE,BE=CF,
求证:△ABF≌△DCE ∠A=∠D相等吗?
当堂测评
A
B
M
C
N
证明:∵△ABN是等腰三角形(已知)
∴AB=AN(等腰三角形腰相等)
又∵BM=NC(已知)
∴BM+MC=NC+MC(等式性质)
即BC=NM
在△ABC与△ANM中
AB=AN(已证)
BC=NM(已证)
AC=AM(已知)
∴△ABC≌△ANM(SSS)
∴∠BAC=∠NAM(全等三角形的对应角相等)
已知:等腰△ABN中,MC是底BN上的两点,且AM=AC,BM=NC。
求证:∠BAC=∠NAM。
挑战自我
通过这节课的学习,你有什么收获和体会?还有什么疑问吗?
总结:
1、“SSS” ,三角形的稳定性及其应用。
2、证角(或线段)相等转化为证角(或线段)所在的三角形全等;
必做题:如图,在四边形ABCD中,AB=CD,AD=CB,求证:∠ A= ∠ C.
D
A
B
C
证明:在△ABD和△CDB中
AB=CD
AD=CB
BD=DB
∴△ABD≌△ACD(SSS)
(已知)
(已知)
(公共边)
∴ ∠ A= ∠ C (全等三角形的对应角相等)
选做题:1、你能说明AB∥CD,AD∥BC吗?
推荐作业:
解:
①∵E、F分别是AB,CD的中点( )
又∵AB=CD
∴AE=CF
在△ADE与△CBF中
AE=
=
∴△ADE≌△CBF ( )
∴AE= AB CF= CD( )
1
2
1
2
选做题:
2、如图,已知AB=CD,AD=CB,E、F分别是AB,CD的中点,且DE=BF,说出下列判断成立的理由.
①△ADE≌△CBF
②∠A=∠C
线段中点的定义
CF
AD
AB
CD
SSS
△ADE≌△CBF
全等三角形对应角相等
已知
A
D
B
C
F
E
CB
② ∵
∴ ∠A=∠C ( )
=
再见
§13.2 三角形全等的条件(一)
教师 鲁玲
我们是最棒的!Come on!
全等三角形的对应边相等,对应角相等。
∵△ABC≌ △DFE
∴ AB=DF, BC=FE, AC=DE
( )
∴ ∠ A= ∠ D, ∠ B= ∠ F ,
∠ C= ∠ E
( )
1、全等三角形的性质
全等三角形的对应边相等
全等三角形的对应角相等
2、三角形全等应具备什么条件?
“边边边”
如何用符号语言来表达呢
在△ABC与△DEF中
A
B
C
D
E
F
AB=DE
AC=DF
BC=EF
∴△ABC≌△DEF(SSS)
这节课让我们用“边边边”定理来判定三角形全等
证明:∵D是BC的中点(已知)
∴BD=CD (中点性质)
在△ABD与△ACD中
AB=AC(已知)
BD=CD(已证)
AD=AD(公共边)
∴△ABD≌△ACD(SSS)
已知:AB=AC, D是BC的中点
求证:△ABD≌△ACD
A
B
C
D
间接条件转化直接条件
明确范围
列齐条件
得出结论
直接条件
间接条件转化而来
暗含条件
已知:AC=FE,BC=DE,AD=FB
求证: ∠ A= ∠ F
证明:∵AD=FB(已知) 间接条件转化
∴AD+DB=FB+BD(等式性质) 为直接条件
即AB=FD
在△ABC和△FDE中, 明确范围
AB=FD(已证)
BC=DE(已知) 列齐条件
AC=FE(已知)
∴△ABC≌△FDE(SSS) 得出结论
∴∠A=∠F(全等三角形的对应角相等)
A
D
B E F C
已知:AB=DC,AF=DE,BE=CF,
求证:△ABF≌△DCE ∠A=∠D相等吗?
1,当堂测评
A
B
M
C
N
已知:等腰△ABN中,M,C是底BN上的两点, 且AM=AC,BM=NC。
求证:∠BAC=∠NAM。
选做题
2,挑战自我
必做题
A
D
B E F C
证明:∵BE=CF(已知) (5分+5分)
∴BE+EF=CF+FE(等式性质) ( 5分+5分)
即BF=CE ( 10分)
在△ABF与△DCE中, ( 10分)
AB=DC(已知) ( 5分+5分)
(10分) BF=CE(已证) ( 5分+5分)
AF=DE(已知) ( 5分+5分)
∴△ABF≌△DCE(SSS) ( 5分+5分)
∴∠A=∠D(全等三角形的对应角相等) ( 5分+5分)
已知:AB=DC,AF=DE,BE=CF,
求证:△ABF≌△DCE ∠A=∠D相等吗?
当堂测评
A
B
M
C
N
证明:∵△ABN是等腰三角形(已知)
∴AB=AN(等腰三角形腰相等)
又∵BM=NC(已知)
∴BM+MC=NC+MC(等式性质)
即BC=NM
在△ABC与△ANM中
AB=AN(已证)
BC=NM(已证)
AC=AM(已知)
∴△ABC≌△ANM(SSS)
∴∠BAC=∠NAM(全等三角形的对应角相等)
已知:等腰△ABN中,MC是底BN上的两点,且AM=AC,BM=NC。
求证:∠BAC=∠NAM。
挑战自我
通过这节课的学习,你有什么收获和体会?还有什么疑问吗?
总结:
1、“SSS” ,三角形的稳定性及其应用。
2、证角(或线段)相等转化为证角(或线段)所在的三角形全等;
必做题:如图,在四边形ABCD中,AB=CD,AD=CB,求证:∠ A= ∠ C.
D
A
B
C
证明:在△ABD和△CDB中
AB=CD
AD=CB
BD=DB
∴△ABD≌△ACD(SSS)
(已知)
(已知)
(公共边)
∴ ∠ A= ∠ C (全等三角形的对应角相等)
选做题:1、你能说明AB∥CD,AD∥BC吗?
推荐作业:
解:
①∵E、F分别是AB,CD的中点( )
又∵AB=CD
∴AE=CF
在△ADE与△CBF中
AE=
=
∴△ADE≌△CBF ( )
∴AE= AB CF= CD( )
1
2
1
2
选做题:
2、如图,已知AB=CD,AD=CB,E、F分别是AB,CD的中点,且DE=BF,说出下列判断成立的理由.
①△ADE≌△CBF
②∠A=∠C
线段中点的定义
CF
AD
AB
CD
SSS
△ADE≌△CBF
全等三角形对应角相等
已知
A
D
B
C
F
E
CB
② ∵
∴ ∠A=∠C ( )
=
再见
