北师大版数学八年级下册6.4.1 多边形的内角和 课件(22张)
文档属性
| 名称 | 北师大版数学八年级下册6.4.1 多边形的内角和 课件(22张) |  | |
| 格式 | pptx | ||
| 文件大小 | 283.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 16:27:03 | ||
图片预览






文档简介
第六章 平行四边形
4 多边形的内角和与外角和
课时1 多边形的内角和
多边形的内角和
正多边形的内角和(重点、难点)
学习目标
新课导入
三角形的内角和是多少?
新课讲解
知识点1 多边形的内角和
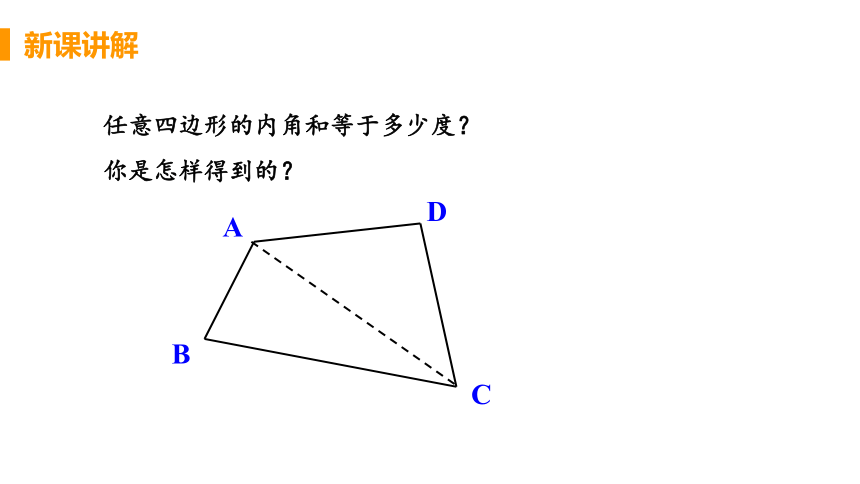
我们知道,三角形的内角和等于180°,正方形、
长方形的内角和都 等于360°.那么,任意一个四边形
的内角和是否也等于360°呢?你能利用 三角形内角
和定理证明四边形的内角和等于360°吗?
新课讲解
任意四边形的内角和等于多少度?
你是怎样得到的?
A
B
D
C
新课讲解
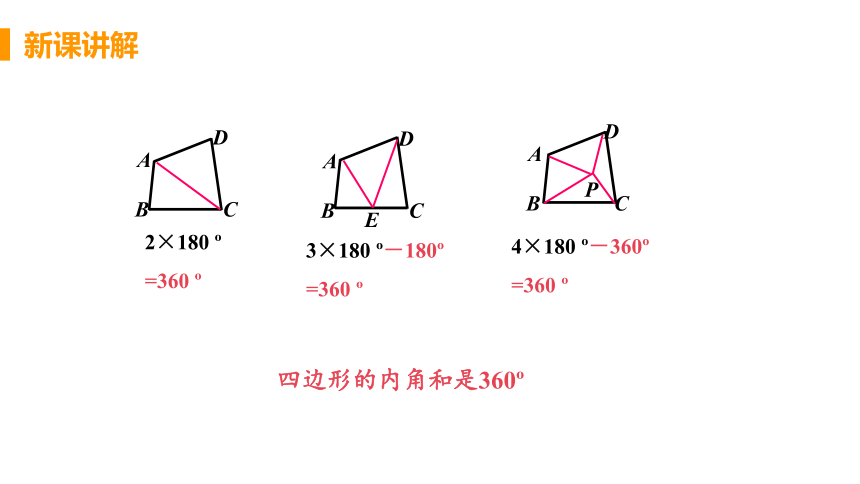
四边形的内角和是360?
A
B
C
D
A
B
C
D
A
B
C
D
E
P
2×180 ?
=360 ?
4×180 ?-360?
=360 ?
3×180 ?-180?
=360 ?
新课讲解
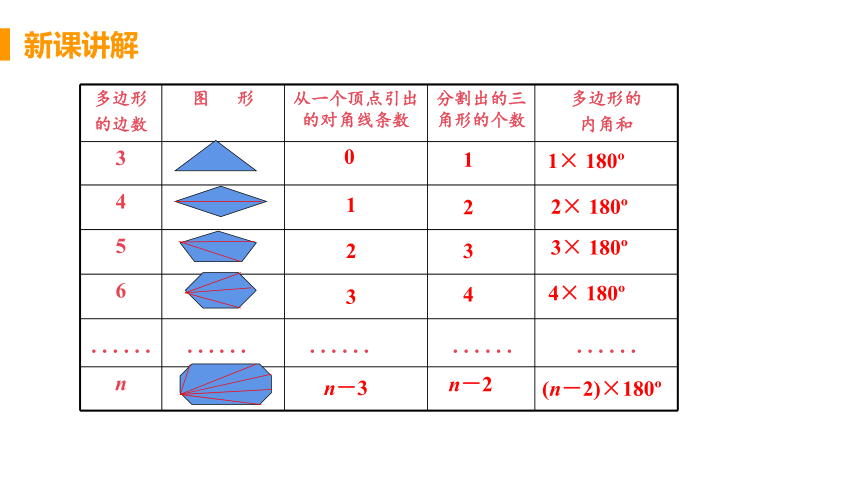
多边形
的边数
图 形
从一个顶点引出的对角线条数
分割出的三角形的个数
多边形的
内角和
3
4
5
6
……
……
……
……
……
n
(n-2)×180?
4× 180?
2× 180?
3× 180?
1× 180?
0
1
1
2
2
3
3
4
n-3
n-2
新课讲解
一般地,从n边形的一个顶点出发,可以作(n - 3)
条对角线,它们将n边形分为(n - 2)个三角形,n边形
的内角和等于180°×(n - 2).
把一个多边形分成几个三角
形,还有其他分法吗?由新
的分法,能得出多边 形内角
和公式吗?
新课讲解
例
典例分析
∵四边形的内角和为(4-2)×180°=360°,
∴∠B=360°-(∠A+∠C+∠D)
=360°-280°
=80°.
分析:
在四边形ABCD中,若∠A+∠C+∠D=280°,则∠B的度数是( )
A.80° B.90° C.170° D.20°
A
新课讲解
例
典例分析
如图,在四边形ABCD中,∠A+∠C=180°.
∠B 与∠D有怎样的关系?
解:
∵ ∠A+∠B+∠C+∠D
=(4-2)×180°=360°,
∴∠B+∠D
=360°-(∠A+∠C)
=360°-180°
=180°.
新课讲解
练一练
内角和为540°的多边形是( )
C
新课讲解
知识点2 正多边形的内角和
正三角形(等边三角形)、正四边形(正方形)、
正五边形、正六边形、正八边形的内角分别是多少度?
剪掉一张长方形纸片的一个角后,纸片还剩几个角?
这个多边形的内角和是多少度?与同伴交流.
新课讲解
正n边形的每个内角的度数为
新课讲解
例
典例分析
若一个多边形的内角和是1 260°,则这个多边形的边数是________.
设这个多边形的边数为n,由题意知,
(n-2)×180°=1 260°,解得n=9.
分析:
9
新课讲解
例
典例分析
如图,求∠A+∠ABC+∠C+∠D+∠E+∠F的度数.
要求不规则图形的各个角的度数和,
就是想办法在不规则图形中找规则
图形,然后把不规则图形的角通过
已学的相关知识(本例中三角形外角
的性质)转移到规则的图形中去,即
把所求的六个角的和转移到四边形
BEFG中去.
分析:
新课讲解
在四边形BEFG中,
∵∠EBG=∠C+∠D,
∠BGF=∠A+∠ABC,
∴∠A+∠ABC+∠C+∠D+∠E+∠F
=∠BGF+∠EBG+∠E+∠F=360°.
解:
新课讲解
练一练
若正多边形的一个内角是150°,则该正多边形的边数是( )
A.6 B.12
C.16 D.18
B
课堂小结
(1)正n边形的每个内角都相等,都等于
(2)n边形的内角和与边数有关,每增加一条边,内角
和就增加180°.
(3)利用公式,已知n边形的边数可求内角和,同样已
知内角和也可求边数.
当堂小练
小彬求出一个正多边形的一个内角为145°. 他的计算正确吗?如果正确,他求的是正几边形
的内角?如果不正确,请说明理由.
不正确.
理由:假设是正n边形,由多边形的内角和定理,得(n-2)×180°=n×145°,
解得n= ,不是整数,所以不正确.
解:
当堂小练
将一个n边形变成(n+1)边形,则内角和将( )
A.减少180° B.增加90°
C.增加180° D.增加360°
C
拓展与延伸
一个多边形除一个内角外其余内角的和为
1 510°,则这个多边形对角线的条数是( )
A.27 B.35
C.44 D.54
C
布置作业
请完成对应习题
4 多边形的内角和与外角和
课时1 多边形的内角和
多边形的内角和
正多边形的内角和(重点、难点)
学习目标
新课导入
三角形的内角和是多少?
新课讲解
知识点1 多边形的内角和
我们知道,三角形的内角和等于180°,正方形、
长方形的内角和都 等于360°.那么,任意一个四边形
的内角和是否也等于360°呢?你能利用 三角形内角
和定理证明四边形的内角和等于360°吗?
新课讲解
任意四边形的内角和等于多少度?
你是怎样得到的?
A
B
D
C
新课讲解
四边形的内角和是360?
A
B
C
D
A
B
C
D
A
B
C
D
E
P
2×180 ?
=360 ?
4×180 ?-360?
=360 ?
3×180 ?-180?
=360 ?
新课讲解
多边形
的边数
图 形
从一个顶点引出的对角线条数
分割出的三角形的个数
多边形的
内角和
3
4
5
6
……
……
……
……
……
n
(n-2)×180?
4× 180?
2× 180?
3× 180?
1× 180?
0
1
1
2
2
3
3
4
n-3
n-2
新课讲解
一般地,从n边形的一个顶点出发,可以作(n - 3)
条对角线,它们将n边形分为(n - 2)个三角形,n边形
的内角和等于180°×(n - 2).
把一个多边形分成几个三角
形,还有其他分法吗?由新
的分法,能得出多边 形内角
和公式吗?
新课讲解
例
典例分析
∵四边形的内角和为(4-2)×180°=360°,
∴∠B=360°-(∠A+∠C+∠D)
=360°-280°
=80°.
分析:
在四边形ABCD中,若∠A+∠C+∠D=280°,则∠B的度数是( )
A.80° B.90° C.170° D.20°
A
新课讲解
例
典例分析
如图,在四边形ABCD中,∠A+∠C=180°.
∠B 与∠D有怎样的关系?
解:
∵ ∠A+∠B+∠C+∠D
=(4-2)×180°=360°,
∴∠B+∠D
=360°-(∠A+∠C)
=360°-180°
=180°.
新课讲解
练一练
内角和为540°的多边形是( )
C
新课讲解
知识点2 正多边形的内角和
正三角形(等边三角形)、正四边形(正方形)、
正五边形、正六边形、正八边形的内角分别是多少度?
剪掉一张长方形纸片的一个角后,纸片还剩几个角?
这个多边形的内角和是多少度?与同伴交流.
新课讲解
正n边形的每个内角的度数为
新课讲解
例
典例分析
若一个多边形的内角和是1 260°,则这个多边形的边数是________.
设这个多边形的边数为n,由题意知,
(n-2)×180°=1 260°,解得n=9.
分析:
9
新课讲解
例
典例分析
如图,求∠A+∠ABC+∠C+∠D+∠E+∠F的度数.
要求不规则图形的各个角的度数和,
就是想办法在不规则图形中找规则
图形,然后把不规则图形的角通过
已学的相关知识(本例中三角形外角
的性质)转移到规则的图形中去,即
把所求的六个角的和转移到四边形
BEFG中去.
分析:
新课讲解
在四边形BEFG中,
∵∠EBG=∠C+∠D,
∠BGF=∠A+∠ABC,
∴∠A+∠ABC+∠C+∠D+∠E+∠F
=∠BGF+∠EBG+∠E+∠F=360°.
解:
新课讲解
练一练
若正多边形的一个内角是150°,则该正多边形的边数是( )
A.6 B.12
C.16 D.18
B
课堂小结
(1)正n边形的每个内角都相等,都等于
(2)n边形的内角和与边数有关,每增加一条边,内角
和就增加180°.
(3)利用公式,已知n边形的边数可求内角和,同样已
知内角和也可求边数.
当堂小练
小彬求出一个正多边形的一个内角为145°. 他的计算正确吗?如果正确,他求的是正几边形
的内角?如果不正确,请说明理由.
不正确.
理由:假设是正n边形,由多边形的内角和定理,得(n-2)×180°=n×145°,
解得n= ,不是整数,所以不正确.
解:
当堂小练
将一个n边形变成(n+1)边形,则内角和将( )
A.减少180° B.增加90°
C.增加180° D.增加360°
C
拓展与延伸
一个多边形除一个内角外其余内角的和为
1 510°,则这个多边形对角线的条数是( )
A.27 B.35
C.44 D.54
C
布置作业
请完成对应习题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
