北师大版数学八年级下册6.4.2 多边形的外角和 课件(18张)
文档属性
| 名称 | 北师大版数学八年级下册6.4.2 多边形的外角和 课件(18张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 282.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 00:00:00 | ||
图片预览






文档简介
第六章 平行四边形
4 多边形的内角和与外角和
课时2 多边形的外角和
多边形的外角和
多边形内角和与外角和的关系(重点、难点)
学习目标
新课导入
三角形的外角和是多少?
新课讲解
知识点1 多边形的外角和
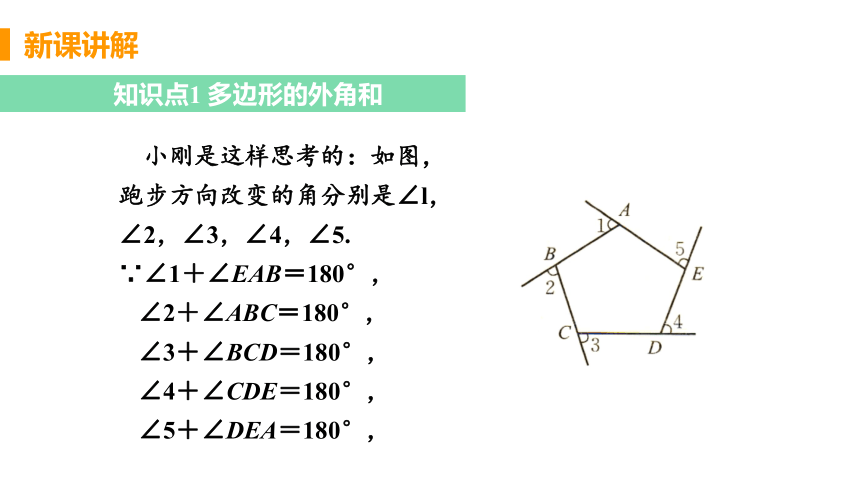
小刚是这样思考的:如图,
跑步方向改变的角分别是∠l,
∠2,∠3,∠4,∠5.
∵∠1+∠EAB=180°,
∠2+∠ABC=180°,
∠3+∠BCD=180°,
∠4+∠CDE=180°,
∠5+∠DEA=180°,
新课讲解
∴∠1+∠EAB+∠2+∠ABC +∠3+∠BCD +∠4+∠CDE +∠5+∠DEA=900°.
∵五边形的内角和为(5-2)×180°=540°,
即 ∠EAB+∠ABC+∠BCD+∠CDE+∠DEA
=540°.
∴∠1+∠2+∠3+∠4+∠5=900°-540°=360°.
你的思路与小刚一样吗?与同伴交流.
新课讲解
如果广场的形状是六边形、八边形,那么结果
会怎样?
新课讲解
1.定义:多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角,在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和.
2.定理:多边形的外角和都等于360°.
新课讲解
例
典例分析
由四边形外角和定理和各外角之间的比例关系可求出各外角.
分析:
已知四边形的四个外角度数比为1∶2∶3∶4,求各外角的度数.
设四边形的最小外角为x°,则其他三个外角分别为2x°,3x°,4x°. 根据四边形外角和等于360°,
得x°+2x°+3x°+4x°=360°.
所以x°=36°,2x°=72°,3x°=108°,4x°=144°.
所以四边形各外角的度数分别为
36°,72°,108°,144°.
解:
新课讲解
练一练
五边形的外角和等于( )
A.180° B.360°
C.540° D.720°
B
新课讲解
知识点2 多边形内角和与外角和的关系
多边形的内(外)角和与边数间的关系:
(1)多边形的内角与边数有关,且随着边数的增加而
增加.
(2)多边形的外角和恒等于360°,与边数的多少无关,
其作用是:
①已知正多边形外角的度数,求正多边形的边数;
②已知正多边形的边数,求各相等外角的度数.
新课讲解
例
典例分析
一个多边形的内角和等于它的外角和的3倍,它是几边形?
设这个多边形是n边形,
则它的内角和是(n-2)·180°,外角和等于 360°.
根据题意,得 (n-2)·180°=3×360°.
解得n=8.
所以,这个多边形是八边形.
解:
新课讲解
例
典例分析
如图,小亮从A点出发,沿直线前进10 m后向左转30°,再沿直线前进10 m,又向左转30°……照这样走下去,小亮第一次回到出发地A点时,他一共走了________.
由题意知,当小亮第一次回
到出发地A点时,所走过的
路线构成一个边长为10 m,
每个外角都是30°的正多边
形.由多边形的外角和定理
知这个多边形的边数是
360°÷30°=12,
所以小亮一共走了120 m.
分析:
120 m
新课讲解
练一练
已知一个多边形的内角和等于它的外角和,则这个多边形的边数为( )
A.3 B.4
C.5 D.6
B
课堂小结
1.多边形的外角和为360°.
2.多边形的内(外)角和与边数间的关系:
(1)多边形的内角与边数有关,且随着边数的增加而增加.
(2)多边形的外角和恒等于360°,与边数的多少无关,其
作用是:
①已知正多边形外角的度数,求正多边形的边数;
②已知正多边形的边数,求各相等外角的度数.
当堂小练
如果正n边形每一个内角等于与它相邻外角的2倍,则n的值是( )
A.4 B.5
C.6 D.7
C
当堂小练
一个多边形的内角和比其外角和的2倍多180°,则该多边形的对角线的条数是( )
A.12 B.13
C.14 D.15
C
拓展与延伸
一个多边形的内角和是外角和的2倍,这个多边形是( )
A.四边形 B.五边形
C.六边形 D.八边形
C
布置作业
请完成对应习题
4 多边形的内角和与外角和
课时2 多边形的外角和
多边形的外角和
多边形内角和与外角和的关系(重点、难点)
学习目标
新课导入
三角形的外角和是多少?
新课讲解
知识点1 多边形的外角和
小刚是这样思考的:如图,
跑步方向改变的角分别是∠l,
∠2,∠3,∠4,∠5.
∵∠1+∠EAB=180°,
∠2+∠ABC=180°,
∠3+∠BCD=180°,
∠4+∠CDE=180°,
∠5+∠DEA=180°,
新课讲解
∴∠1+∠EAB+∠2+∠ABC +∠3+∠BCD +∠4+∠CDE +∠5+∠DEA=900°.
∵五边形的内角和为(5-2)×180°=540°,
即 ∠EAB+∠ABC+∠BCD+∠CDE+∠DEA
=540°.
∴∠1+∠2+∠3+∠4+∠5=900°-540°=360°.
你的思路与小刚一样吗?与同伴交流.
新课讲解
如果广场的形状是六边形、八边形,那么结果
会怎样?
新课讲解
1.定义:多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角,在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和.
2.定理:多边形的外角和都等于360°.
新课讲解
例
典例分析
由四边形外角和定理和各外角之间的比例关系可求出各外角.
分析:
已知四边形的四个外角度数比为1∶2∶3∶4,求各外角的度数.
设四边形的最小外角为x°,则其他三个外角分别为2x°,3x°,4x°. 根据四边形外角和等于360°,
得x°+2x°+3x°+4x°=360°.
所以x°=36°,2x°=72°,3x°=108°,4x°=144°.
所以四边形各外角的度数分别为
36°,72°,108°,144°.
解:
新课讲解
练一练
五边形的外角和等于( )
A.180° B.360°
C.540° D.720°
B
新课讲解
知识点2 多边形内角和与外角和的关系
多边形的内(外)角和与边数间的关系:
(1)多边形的内角与边数有关,且随着边数的增加而
增加.
(2)多边形的外角和恒等于360°,与边数的多少无关,
其作用是:
①已知正多边形外角的度数,求正多边形的边数;
②已知正多边形的边数,求各相等外角的度数.
新课讲解
例
典例分析
一个多边形的内角和等于它的外角和的3倍,它是几边形?
设这个多边形是n边形,
则它的内角和是(n-2)·180°,外角和等于 360°.
根据题意,得 (n-2)·180°=3×360°.
解得n=8.
所以,这个多边形是八边形.
解:
新课讲解
例
典例分析
如图,小亮从A点出发,沿直线前进10 m后向左转30°,再沿直线前进10 m,又向左转30°……照这样走下去,小亮第一次回到出发地A点时,他一共走了________.
由题意知,当小亮第一次回
到出发地A点时,所走过的
路线构成一个边长为10 m,
每个外角都是30°的正多边
形.由多边形的外角和定理
知这个多边形的边数是
360°÷30°=12,
所以小亮一共走了120 m.
分析:
120 m
新课讲解
练一练
已知一个多边形的内角和等于它的外角和,则这个多边形的边数为( )
A.3 B.4
C.5 D.6
B
课堂小结
1.多边形的外角和为360°.
2.多边形的内(外)角和与边数间的关系:
(1)多边形的内角与边数有关,且随着边数的增加而增加.
(2)多边形的外角和恒等于360°,与边数的多少无关,其
作用是:
①已知正多边形外角的度数,求正多边形的边数;
②已知正多边形的边数,求各相等外角的度数.
当堂小练
如果正n边形每一个内角等于与它相邻外角的2倍,则n的值是( )
A.4 B.5
C.6 D.7
C
当堂小练
一个多边形的内角和比其外角和的2倍多180°,则该多边形的对角线的条数是( )
A.12 B.13
C.14 D.15
C
拓展与延伸
一个多边形的内角和是外角和的2倍,这个多边形是( )
A.四边形 B.五边形
C.六边形 D.八边形
C
布置作业
请完成对应习题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
