人教版八年级下册数学 17.2勾股定理的逆定理 同步练习(Word版 含解析)
文档属性
| 名称 | 人教版八年级下册数学 17.2勾股定理的逆定理 同步练习(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 94.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 00:23:22 | ||
图片预览


文档简介
17.2勾股定理的逆定理 同步练习
一.选择题
1.以下列各组数据为三角形三边,能构成直角三角形的是( )
A.4cm,8cm,7cm B.3cm,5cm,2cm
C.2cm,2cm,4cm D.13cm,12cm,5cm
2.满足下列条件的△ABC,不是直角三角形的是( )
A.b2﹣c2=a2 B.a:b:c=5:12:13
C.∠A:∠B:∠C=3:4:5 D.∠C=∠A﹣∠B
3.三角形三边长分别为①3,4,5②5,12,13③17,8,15④1,3,2.其中直角三角形有( )
A.1个 B.2个 C.3个 D.4个
4.如图,是一种饮料的包装盒,长、宽、高分别为4cm、3cm、12cm,现有一长为16cm的吸管插入到盒的底部,则吸管露在盒外的部分h的取值范围为( )
A.3<h<4 B.3≤h≤4 C.2≤h≤4 D.h=4
5.下列结论中,正确的有( )
①△ABC的三边长分别为a,b,c,若b2+c2=a2,则△ABC是直角三角形;
②在Rt△ABC中,已知两边长分别为6和8,则第三边的长为10;
③在△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形;
④若三角形的三边长之比为1:2:,则该三角形是直角三角形.
A.3个 B.2个 C.1个 D.0个
6.下列四组数中,是勾股数的是( )
A.0.3,0.4,0.5 B.32,42,52
C.30,40,50 D.,,
7.如图,在边长为1的正方形方格中,A,B,C,D均为格点,构成图中三条线段AB,BC,CD.现在取出这三条线段AB,BC,CD首尾相连拼三角形.下列判断正确的是( )
A.能拼成一个直角三角形 B.能拼成一个锐角三角形
C.能拼成一个钝角三角形 D.不能拼成三角形
8.如图,原来从A村到B村,需要沿路A→C→B(∠C=90°)绕过村庄间的一座大山.打通A,B间的隧道后,就可直接从A村到B村.已知,AC=12km,BC=16km,那么,打通隧道后从A村到B村比原来减少的路程为( )
A.5km B.8km C.10km D.20km
9.下列三角形中,是直角三角形的是( )
A.三角形的三边a,b,c满足关系a+b>c
B.三角形的三边长分别为32,42,52
C.三角形的一边等于另一边的一半
D.三角形的三边长为20,15,25
10.如图,在△ABC中,AC=8,BC=6,AB=10,P为边AB上一动点,PD⊥AC于D,PE⊥BC于E,则DE的最小值为( )
A.3.6 B.4.8 C.5 D.5.2
二.填空题
11.若一个三角形的三边长为1、2、x,则使此三角形是直角三角形的x的值是 .
12.在△ABC中,给出以下4个条件:
①∠C=90°;
②∠A+∠B=∠C;
③a:b:c=3:4:5;
④∠A:∠B:∠C=3:4:5.
从中任取一个条件,可以判定出△ABC是直角三角形的有 .(填序号)
13.已知三角形的两条较短边的长分别为6和8,当第三边的长为 时,此三角形是直角三角形.
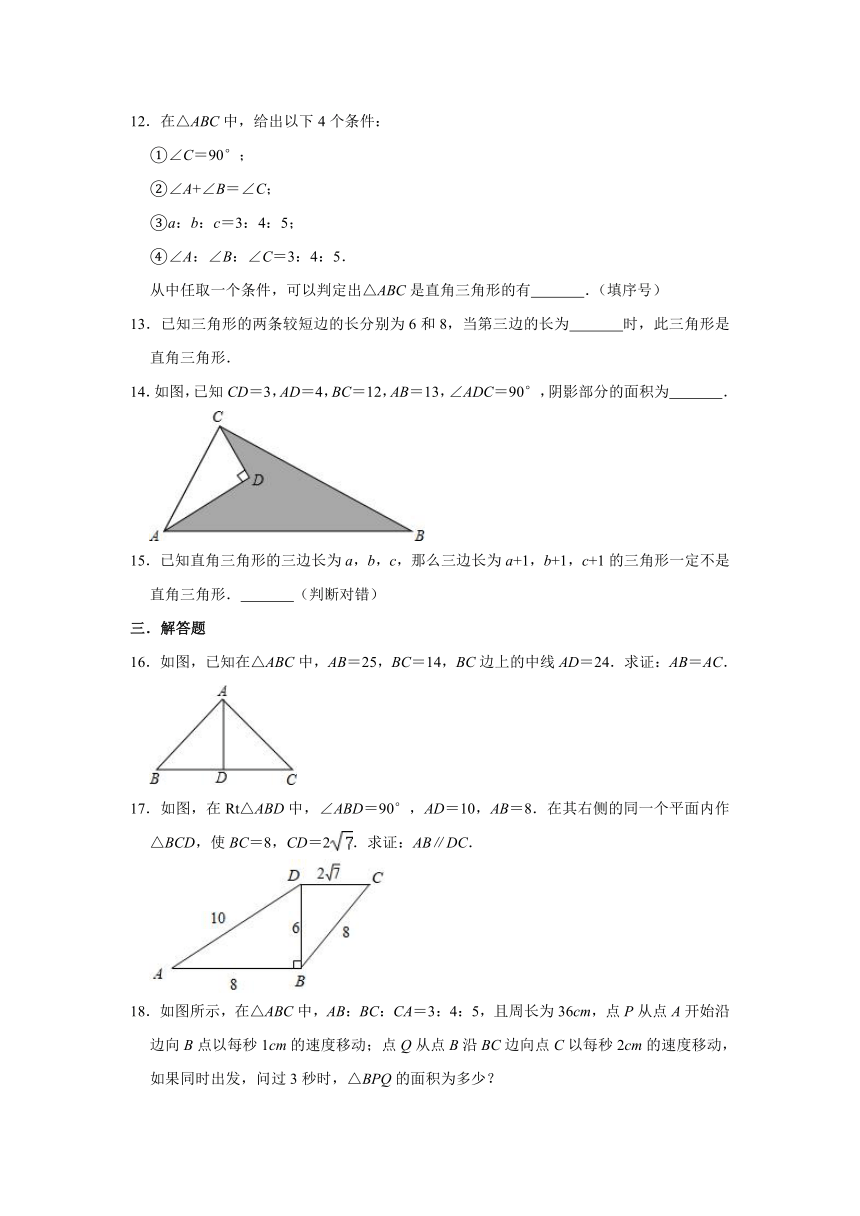
14.如图,已知CD=3,AD=4,BC=12,AB=13,∠ADC=90°,阴影部分的面积为 .
15.已知直角三角形的三边长为a,b,c,那么三边长为a+1,b+1,c+1的三角形一定不是直角三角形. (判断对错)
三.解答题
16.如图,已知在△ABC中,AB=25,BC=14,BC边上的中线AD=24.求证:AB=AC.
17.如图,在Rt△ABD中,∠ABD=90°,AD=10,AB=8.在其右侧的同一个平面内作△BCD,使BC=8,CD=2.求证:AB∥DC.
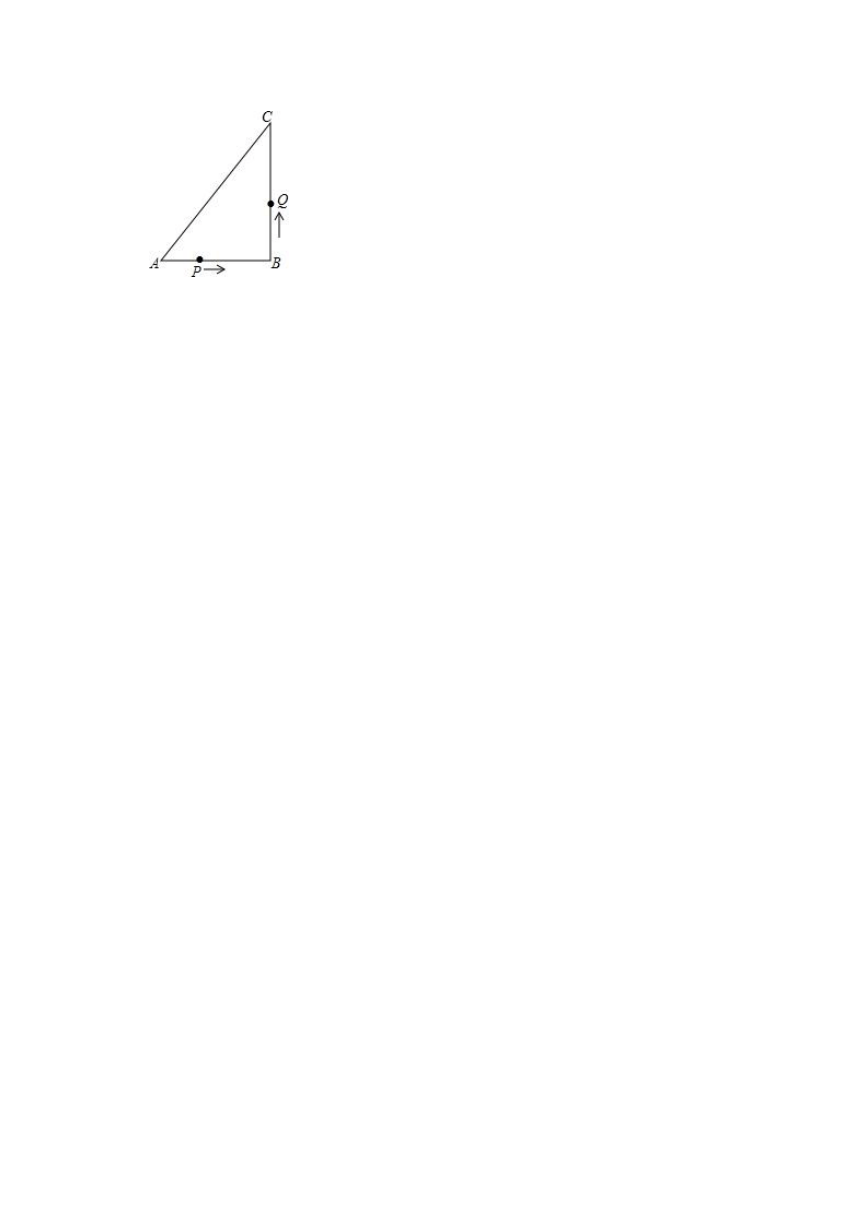
18.如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36cm,点P从点A开始沿边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,问过3秒时,△BPQ的面积为多少?
参考答案
一.选择题
1.解:A、42+72≠82,故不能构成直角三角形;
B、2+3=5,故不能构成三角形,不能构成直角三角形;
C、2+2=4,故不能构成三角形,不能构成直角三角形;
D、52+122=132,故能构成直角三角形;
故选:D.
2.解:A、由b2﹣c2=a2,可得:b2=c2+a2,是直角三角形,故本选项错误;
B、由a:b:c=5:12:13,可得(5x)2+(12x)2=(13x)2,是直角三角形,故本选项错误;
C、由∠A:∠B:∠C=3:4:5,可得:∠C=75°,不是直角三角形,故选项正确;
D、由∠C=∠A﹣∠B,可得∠A=90°,是直角三角形,故本选项错误;
故选:C.
3.解:①32+42=52,符合勾股定理的逆定理,能构成直角三角形;
②52+122=132,符合勾股定理的逆定理,能构成直角三角形;
③82+152=172,符合勾股定理的逆定理,能构成直角三角形;
④12+(2)2=32,符合勾股定理的逆定理,能构成直角三角形.
故选:D.
4.解:①当吸管放进杯里垂直于底面时露在杯口外的长度最长,最长为16﹣12=4(cm);
②露出部分最短时与底面对角线和高正好组成直角三角形,
底面对角线直径为5cm,高为12cm,
由勾股定理可得杯里面管长为=13cm,则露在杯口外的长度最长为16﹣13=3cm;
则可得露在杯口外的长度在3cm和4cm范围变化.
故选:B.
5.解:①△ABC的三边长分别为a,b,c,若b2+c2=a2,则△ABC是直角三角形,选项说法正确;
②在Rt△ABC中,已知两边长分别为6和8,则第三边的长为10或2,选项说法错误;
③在△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形,选项说法正确;
④若三角形的三边长之比为1:2:,则该三角形是直角三角形,选项说法正确;
故选:A.
6.解:A.0.3,0.4,0.5不是整数,不是勾股数;
B.(32)2+(42)2=337≠(52)2,∴32,42,52不是勾股数;
C.∵302+402=2500=502,∴30、40、50是勾股数;
D.2+()2≠()2且,,均不是整数,∴,,不是勾股数;
故选:C.
7.解:由网格图可得:
AB2=22+32=4+9=13,
CB2=22+12=4+1=5,
CD2=22+22=4+4=8,
∴CB2+CD2=5+8=13=AB2,
∴线段AB,BC,CD首尾相连拼成的三角形是直角三角形,
故选:A.
8.解:由题意可得:AB===20(km),
则打通隧道后从A村到B村比原来减少的路程为:12+16﹣20=8(km).
故选:B.
9.解:A、三角形的三边满足关系a+b>c,不符合勾股定理的逆定理,故本选项不符合题意;
B、∵(32)2+(42)2≠(52)2,∴此三角形不是直角三角形,故本选项不符合题意;
C、三角形的一边等于另一边的一半无法判断三角形的形状,故本选项不符合题意;
D、∵152+202=252,∴此三角形是直角三角形,故本选项符合题意.
故选:D.
10.解:∵△ABC中,∠C=90°,AC=8,BC=6,AB=10,82+62=102,
∴△ABC是直角三角形,∠C=90°,
连接CP,
∵PD⊥AC于D,PE⊥CB于E,
∴四边形DPEC是矩形,
∴DE=CP,
当DE最小时,则CP最小,根据垂线段最短可知当CP⊥AB时,则CP最小,
∴DE=CP==4.8,
故选:B.
二.填空题
11.解:设第三边为x,
(1)若2是直角边,则第三边x是斜边,由勾股定理,得:
12+22=x2,所以x=;
(2)若2是斜边,则第三边x为直角边,由勾股定理,得:
12+x2=22,所以x=;
综上所述:x的值为或,
故答案为:或.
12.解:①∠C=90°,△ABC是直角三角形;
②∵∠A+∠B=∠C,∴∠C=90°,△ABC是直角三角形;
③∵a:b:c=3:4:5,∴(3x)2+(4x)2=(5x)2,△ABC是直角三角形;
④∵∠A:∠B:∠C=3:4:5,∴∠C=,△ABC不是直角三角形;
故答案为:①②③.
13.解:∵三角形的两条较短边的长分别为6和8,
∴当第三边的长为=10时,此三角形是直角三角形.
故答案为:10.
14.解:在Rt△ADC中,由勾股定理得:AC===5,
∵AC=5,AB=13,BC=12,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴阴影部分的面积S=S△ACB﹣S△ADC=
=
=24,
故答案为:24.
15.解:设某直角三角形的两直角边分别是a,b,斜边长为c,
∴a2+b2=c2,
∵(a+1)2+(b+1)2=a2+2a+1+b2+2b+1,(c+1)2=c2+2c+1,
∴(a+1)2+(b+1)2﹣(c+1)2=2a+2b﹣2c+1=2(a+b﹣c)+1,
∵a+b>c,
∴a+b﹣c>0,
∴2(a+b﹣c)+1>1,
∴(a+1)2+(b+1)2﹣(c+1)2>1≠0,
∴三边长分别为a+1,b+1,c+1,三角形不是直角三角形,
故答案为:×.
三.解答题
16.证明:∵AD 是BC边上的中线
∴BD=BC=×14=7,
在△ABD中,BD2+AD2=72+242=625=252=AB2,
∴∠ADB=90°,
∴AD 垂直平分BC,
∴AB=AC.
17.证明:∵在Rt△ABD中,∠ABD=90°,AD=10,AB=8,
∴BD===6,
∵BC=8,CD=2,
∴62+(2)2=82,
∴△BDC是直角三角形,
∴∠BDC=90°,
∴∠ABD=∠BDC,
∴AB∥DC.
18.解:设AB为3xcm,BC为4xcm,AC为5xcm,
∵周长为36cm,
AB+BC+AC=36cm,
∴3x+4x+5x=36,
得x=3,
∴AB=9cm,BC=12cm,AC=15cm,
∵AB2+BC2=AC2,
∴△ABC是直角三角形,
过3秒时,BP=9﹣3×1=6(cm),BQ=2×3=6(cm),
∴S△PBQ=BP?BQ=×6×6=18(cm2).
故过3秒时,△BPQ的面积为18cm2.
一.选择题
1.以下列各组数据为三角形三边,能构成直角三角形的是( )
A.4cm,8cm,7cm B.3cm,5cm,2cm
C.2cm,2cm,4cm D.13cm,12cm,5cm
2.满足下列条件的△ABC,不是直角三角形的是( )
A.b2﹣c2=a2 B.a:b:c=5:12:13
C.∠A:∠B:∠C=3:4:5 D.∠C=∠A﹣∠B
3.三角形三边长分别为①3,4,5②5,12,13③17,8,15④1,3,2.其中直角三角形有( )
A.1个 B.2个 C.3个 D.4个
4.如图,是一种饮料的包装盒,长、宽、高分别为4cm、3cm、12cm,现有一长为16cm的吸管插入到盒的底部,则吸管露在盒外的部分h的取值范围为( )
A.3<h<4 B.3≤h≤4 C.2≤h≤4 D.h=4
5.下列结论中,正确的有( )
①△ABC的三边长分别为a,b,c,若b2+c2=a2,则△ABC是直角三角形;
②在Rt△ABC中,已知两边长分别为6和8,则第三边的长为10;
③在△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形;
④若三角形的三边长之比为1:2:,则该三角形是直角三角形.
A.3个 B.2个 C.1个 D.0个
6.下列四组数中,是勾股数的是( )
A.0.3,0.4,0.5 B.32,42,52
C.30,40,50 D.,,
7.如图,在边长为1的正方形方格中,A,B,C,D均为格点,构成图中三条线段AB,BC,CD.现在取出这三条线段AB,BC,CD首尾相连拼三角形.下列判断正确的是( )
A.能拼成一个直角三角形 B.能拼成一个锐角三角形
C.能拼成一个钝角三角形 D.不能拼成三角形
8.如图,原来从A村到B村,需要沿路A→C→B(∠C=90°)绕过村庄间的一座大山.打通A,B间的隧道后,就可直接从A村到B村.已知,AC=12km,BC=16km,那么,打通隧道后从A村到B村比原来减少的路程为( )
A.5km B.8km C.10km D.20km
9.下列三角形中,是直角三角形的是( )
A.三角形的三边a,b,c满足关系a+b>c
B.三角形的三边长分别为32,42,52
C.三角形的一边等于另一边的一半
D.三角形的三边长为20,15,25
10.如图,在△ABC中,AC=8,BC=6,AB=10,P为边AB上一动点,PD⊥AC于D,PE⊥BC于E,则DE的最小值为( )
A.3.6 B.4.8 C.5 D.5.2
二.填空题
11.若一个三角形的三边长为1、2、x,则使此三角形是直角三角形的x的值是 .
12.在△ABC中,给出以下4个条件:
①∠C=90°;
②∠A+∠B=∠C;
③a:b:c=3:4:5;
④∠A:∠B:∠C=3:4:5.
从中任取一个条件,可以判定出△ABC是直角三角形的有 .(填序号)
13.已知三角形的两条较短边的长分别为6和8,当第三边的长为 时,此三角形是直角三角形.
14.如图,已知CD=3,AD=4,BC=12,AB=13,∠ADC=90°,阴影部分的面积为 .
15.已知直角三角形的三边长为a,b,c,那么三边长为a+1,b+1,c+1的三角形一定不是直角三角形. (判断对错)
三.解答题
16.如图,已知在△ABC中,AB=25,BC=14,BC边上的中线AD=24.求证:AB=AC.
17.如图,在Rt△ABD中,∠ABD=90°,AD=10,AB=8.在其右侧的同一个平面内作△BCD,使BC=8,CD=2.求证:AB∥DC.
18.如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36cm,点P从点A开始沿边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,问过3秒时,△BPQ的面积为多少?
参考答案
一.选择题
1.解:A、42+72≠82,故不能构成直角三角形;
B、2+3=5,故不能构成三角形,不能构成直角三角形;
C、2+2=4,故不能构成三角形,不能构成直角三角形;
D、52+122=132,故能构成直角三角形;
故选:D.
2.解:A、由b2﹣c2=a2,可得:b2=c2+a2,是直角三角形,故本选项错误;
B、由a:b:c=5:12:13,可得(5x)2+(12x)2=(13x)2,是直角三角形,故本选项错误;
C、由∠A:∠B:∠C=3:4:5,可得:∠C=75°,不是直角三角形,故选项正确;
D、由∠C=∠A﹣∠B,可得∠A=90°,是直角三角形,故本选项错误;
故选:C.
3.解:①32+42=52,符合勾股定理的逆定理,能构成直角三角形;
②52+122=132,符合勾股定理的逆定理,能构成直角三角形;
③82+152=172,符合勾股定理的逆定理,能构成直角三角形;
④12+(2)2=32,符合勾股定理的逆定理,能构成直角三角形.
故选:D.
4.解:①当吸管放进杯里垂直于底面时露在杯口外的长度最长,最长为16﹣12=4(cm);
②露出部分最短时与底面对角线和高正好组成直角三角形,
底面对角线直径为5cm,高为12cm,
由勾股定理可得杯里面管长为=13cm,则露在杯口外的长度最长为16﹣13=3cm;
则可得露在杯口外的长度在3cm和4cm范围变化.
故选:B.
5.解:①△ABC的三边长分别为a,b,c,若b2+c2=a2,则△ABC是直角三角形,选项说法正确;
②在Rt△ABC中,已知两边长分别为6和8,则第三边的长为10或2,选项说法错误;
③在△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形,选项说法正确;
④若三角形的三边长之比为1:2:,则该三角形是直角三角形,选项说法正确;
故选:A.
6.解:A.0.3,0.4,0.5不是整数,不是勾股数;
B.(32)2+(42)2=337≠(52)2,∴32,42,52不是勾股数;
C.∵302+402=2500=502,∴30、40、50是勾股数;
D.2+()2≠()2且,,均不是整数,∴,,不是勾股数;
故选:C.
7.解:由网格图可得:
AB2=22+32=4+9=13,
CB2=22+12=4+1=5,
CD2=22+22=4+4=8,
∴CB2+CD2=5+8=13=AB2,
∴线段AB,BC,CD首尾相连拼成的三角形是直角三角形,
故选:A.
8.解:由题意可得:AB===20(km),
则打通隧道后从A村到B村比原来减少的路程为:12+16﹣20=8(km).
故选:B.
9.解:A、三角形的三边满足关系a+b>c,不符合勾股定理的逆定理,故本选项不符合题意;
B、∵(32)2+(42)2≠(52)2,∴此三角形不是直角三角形,故本选项不符合题意;
C、三角形的一边等于另一边的一半无法判断三角形的形状,故本选项不符合题意;
D、∵152+202=252,∴此三角形是直角三角形,故本选项符合题意.
故选:D.
10.解:∵△ABC中,∠C=90°,AC=8,BC=6,AB=10,82+62=102,
∴△ABC是直角三角形,∠C=90°,
连接CP,
∵PD⊥AC于D,PE⊥CB于E,
∴四边形DPEC是矩形,
∴DE=CP,
当DE最小时,则CP最小,根据垂线段最短可知当CP⊥AB时,则CP最小,
∴DE=CP==4.8,
故选:B.
二.填空题
11.解:设第三边为x,
(1)若2是直角边,则第三边x是斜边,由勾股定理,得:
12+22=x2,所以x=;
(2)若2是斜边,则第三边x为直角边,由勾股定理,得:
12+x2=22,所以x=;
综上所述:x的值为或,
故答案为:或.
12.解:①∠C=90°,△ABC是直角三角形;
②∵∠A+∠B=∠C,∴∠C=90°,△ABC是直角三角形;
③∵a:b:c=3:4:5,∴(3x)2+(4x)2=(5x)2,△ABC是直角三角形;
④∵∠A:∠B:∠C=3:4:5,∴∠C=,△ABC不是直角三角形;
故答案为:①②③.
13.解:∵三角形的两条较短边的长分别为6和8,
∴当第三边的长为=10时,此三角形是直角三角形.
故答案为:10.
14.解:在Rt△ADC中,由勾股定理得:AC===5,
∵AC=5,AB=13,BC=12,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴阴影部分的面积S=S△ACB﹣S△ADC=
=
=24,
故答案为:24.
15.解:设某直角三角形的两直角边分别是a,b,斜边长为c,
∴a2+b2=c2,
∵(a+1)2+(b+1)2=a2+2a+1+b2+2b+1,(c+1)2=c2+2c+1,
∴(a+1)2+(b+1)2﹣(c+1)2=2a+2b﹣2c+1=2(a+b﹣c)+1,
∵a+b>c,
∴a+b﹣c>0,
∴2(a+b﹣c)+1>1,
∴(a+1)2+(b+1)2﹣(c+1)2>1≠0,
∴三边长分别为a+1,b+1,c+1,三角形不是直角三角形,
故答案为:×.
三.解答题
16.证明:∵AD 是BC边上的中线
∴BD=BC=×14=7,
在△ABD中,BD2+AD2=72+242=625=252=AB2,
∴∠ADB=90°,
∴AD 垂直平分BC,
∴AB=AC.
17.证明:∵在Rt△ABD中,∠ABD=90°,AD=10,AB=8,
∴BD===6,
∵BC=8,CD=2,
∴62+(2)2=82,
∴△BDC是直角三角形,
∴∠BDC=90°,
∴∠ABD=∠BDC,
∴AB∥DC.
18.解:设AB为3xcm,BC为4xcm,AC为5xcm,
∵周长为36cm,
AB+BC+AC=36cm,
∴3x+4x+5x=36,
得x=3,
∴AB=9cm,BC=12cm,AC=15cm,
∵AB2+BC2=AC2,
∴△ABC是直角三角形,
过3秒时,BP=9﹣3×1=6(cm),BQ=2×3=6(cm),
∴S△PBQ=BP?BQ=×6×6=18(cm2).
故过3秒时,△BPQ的面积为18cm2.
