人教版九年级数学下册 第29章 投影与视图 单元测试题(Word版 有答案)
文档属性
| 名称 | 人教版九年级数学下册 第29章 投影与视图 单元测试题(Word版 有答案) |  | |
| 格式 | docx | ||
| 文件大小 | 248.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 00:38:41 | ||
图片预览

文档简介
1049020010693400123190000第29章 投影与视图 单元测试题
(满分100分;时间:90分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 围成圆形的栏杆的影子都在圈外,则影子是在下列哪种光照射下形成的( )
A.太阳光 B.圈里的路灯的灯光
C.手电筒发出的灯光 D.台灯的灯光
?2. 如图,小强用5个相同的小立方体搭成的立体图形研究几何体的三视图的变化情况,若由图1变到图2,不改变的是( )
A.主视图 B.主视图和左视图
C.主视图和俯视图 D.左视图和俯视图
?3. 三棱柱的三视图如图,△EFG中,EF=8cm,EG=12cm,∠EGF=30?,则AB的长( )
A.6 B.8 C.12 D.33
?
4. 用若干个相同的小正方体搭成一个几何体模型,其主视图与左视图如图所示,则该几何体的俯视图不可能是(? ? ? ? )
A. B. C. D.
?
5. 如图是某几何体的三视图,其侧面积为(? ? ? ? )
A.6 B.4π C.6π D.12π
?
6. 如图是空心圆柱体在指定方向上的视图,正确的是( )
A. B. C. D.
?
7. 如图是某几何体的三视图,则该几何体的侧面积是( )
A.210π B.410π C.15π D.413π
?
8. 右图所示的正三棱柱的主视图的是( )
A. B. C. D.
?
9. 如图是一个“中”的几何体,则该几何体的俯视图为( )
A. B. C. D.
?
10. 如图,把一个棱长为3的正方体的每个面等分成9个小正方形,然后沿每个面正中心的一个正方形向里挖空(相当于挖去7个小正方体),所得到的几何体的表面积是( )
A.78 B.72 C.54 D.48
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
11. 如图是两棵小树在同一时刻的影子,那么图①是________投影,图②是________投影.
?
12. 如图是由五个大小相同的正方体搭成的几何体,从________面看所得到的性状图的面积最小. ?
13. 某几何体的三视图如图,那么该几何体是________.
14. 一个几何体的主视图,左视图,俯视图都是同一个图形,那么这个几何体形状可能是________(填写一个即可). ?
15. 同一时刻,同一地区,太阳光下物体的高度与投影长的比是________.
?
16. 已知两个电线杆在太阳光下形成两条不同的线段,那么这两条线段可能________,也可能________.
?
17. 两个物体在同一灯光下得到的影子构成的两个三角形________相似三角形.(填“是”或“不同是)
?
18. 一个正方体边长2cm,这个正方体的表面积为________cm2,体积为________cm3.
?
19. 如图,这个图形从正面看是________,从左面看是________,从上面看是________. ?
20. 长方体的主视图与左视图如图所示(单位:cm),则其俯视图的面积是________.
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
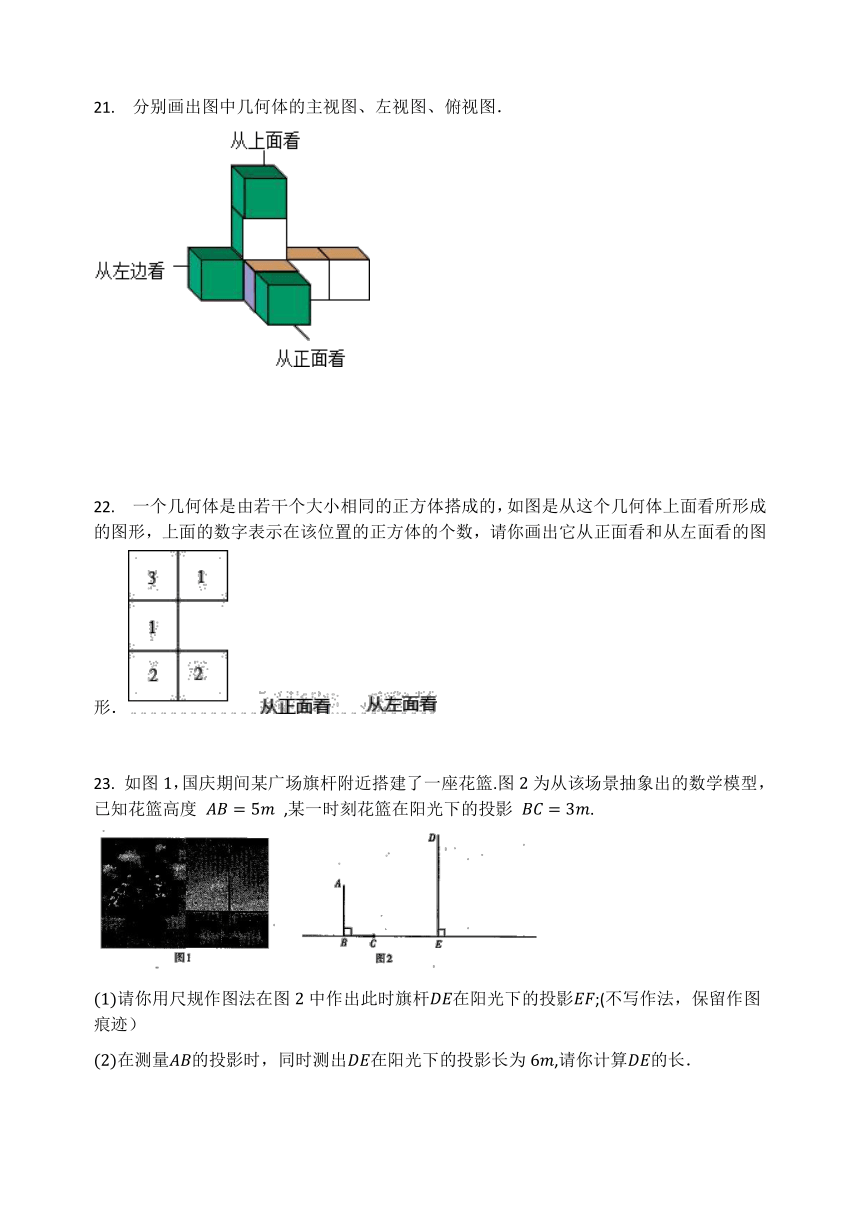
21. 分别画出图中几何体的主视图、左视图、俯视图.
?
22. 一个几何体是由若干个大小相同的正方体搭成的,如图是从这个几何体上面看所形成的图形,上面的数字表示在该位置的正方体的个数,请你画出它从正面看和从左面看的图形.
?
23. 如图1,国庆期间某广场旗杆附近搭建了一座花篮.图2为从该场景抽象出的数学模型,已知花篮高度 AB=5m ,某一时刻花篮在阳光下的投影 BC=3m.
(1)请你用尺规作图法在图2中作出此时旗杆DE在阳光下的投影EF;(不写作法,保留作图痕迹)
(2)在测量AB的投影时,同时测出DE在阳光下的投影长为6m,请你计算DE的长.
?
24. 一个几何体的三视图如图所示,它的俯视图为菱形.请写出该几何体的形状,并根据图中所给的数据求出它的侧面积.
?
25. 如图,窗户的一条边AB在地面上的平行投影为A'B'.将整个窗户的投影补充完整.
?
26. 如图,已知线段AB的长为1,投影面为P.
(1)如图1,当AB平行于投影面P时,它的正投影A'B'的长是多少?
(2)在(1)的基础上,点A不动,线段AB绕着点A在垂直于P的平面内逆时针旋转30?,如图2,这时AB的正投影A'B'将比原来缩短,试求出这时A'B'的长度.
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
B
【解答】
解:因为围成圆形的栏杆的影子都在圈外,所以光源在圈里,即影子是在下圈里的路灯的灯光照射下形成的.故选B.
2.
【答案】
D
【解答】
从上边看得到的图形都是第一层一个小正方形,第二层是三个小正方形,从左边看第一层是两个小正方形,第二层左边一个小正方形,
3.
【答案】
A
【解答】
解:过点E作EQ⊥FG于点Q,
由题意可得出:EQ=AB,
∵ EG=12cm,∠EGF=30?,
∴ EQ=AB=12×12=6(cm).
故选A.
4.
【答案】
D
【解答】
解:根据主视图、左视图,可知A,B,C中的图形均有可能是几何体的俯视图,只有D中的图形不可能是几何体的俯视图.
故选D.
5.
【答案】
C
【解答】
解:观察三视图知:该几何体为圆柱,高为3cm,底面直径为2cm,
∴ 侧面积为:πdh=2π×3=6π.
故选C.
6.
【答案】
C
【解答】
解:圆柱的主视图是矩形,里面有两条用虚线表示的看不到的棱,故选C.
7.
【答案】
B
【解答】
解:由图可得,该几何体为一个圆锥,
根据圆锥的侧面积公式可得πrl=π×2×62+22=410π.
故选B.
8.
【答案】
B
【解答】
解:从正面看三棱柱,是矩形里面一条虚线.故选B.
9.
【答案】
C
【解答】
解:从上边看是由5个矩形组成得,左边矩形的右边是虚线,右边矩形的左边是虚线,
故选:C.
10.
【答案】
B
【解答】
解:如图所示,周边的六个挖空的正方体每个面增加4个正方形,且减少了1个正方形,则每个面的正方形个数为12个,则表面积为12×6×1=72.
故选B.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
平行,中心
【解答】
解:图①是平行投影;
图②是中心投影.
故答案为:平行、中心.
12.
【答案】
左
【解答】
解:从正面看第一层是三个小正方形,第二层左边一个小正方形,共四个小正方形;
从上面看第一层左边一个小正方形,第二层是三个小正方形,共四个小正方形;
从左面看第一层两个小正方形,第二层左边一个小正方形,共三个小正方形,
故答案为:左.
13.
【答案】
圆柱
【解答】
解:∵ 几何体的主视图和俯视图都是宽度相等的长方形,
故该几何体是一个柱体,
又∵ 俯视图是一个圆,
故该几何体是一个圆柱
故答案为:圆柱.
14.
【答案】
正方体或球体(填一个即可)
【解答】
解:依题意,主视图、左视图以及俯视图都相同的几何体是正方体或球体.
15.
【答案】
成正比例的
【解答】
解:同一时刻,同一地区,太阳光下物体的高度与投影长的比是成正比例的.
16.
【答案】
平行,在同一直线上
【解答】
解:当两个电线杆在同一条直线上时,所形成的两条不同的线段在同一直线上,
当两个电线杆不在同一条直线上时,所形成的两条不同的线段平行,
故答案为:平行或在同一直线上.
17.
【答案】
不是
【解答】
解:要使立于地面上的不同的物体与影子构成的三角形相似,必须是平行投影,而灯光是中心投影,所以两个物体在同一灯光下得到的影子构成的两个三角形不是相似三角形.
故答案为:不是.
18.
【答案】
24,8
【解答】
解:2×2×6=24(平方厘米);
2×2×2=8(立方厘米);
答:这个正方体的表面积是24平方厘米,体积是8立方厘米.
故答案为:24,8.
19.
【答案】
梯形,梯形,同心圆环
【解答】
解:该图形从正面看是?梯形,从左面看是梯形,从上面看是同心圆环.
故答案为:梯形,梯形,同心圆环.
20.
【答案】
12(cm2)
【解答】
解:根据题意,正方体的俯视图是矩形,它的长是4cm,宽是3cm,面积=4×3=12(cm2),
故答案为:12(cm2).
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
解:如图所示,
【解答】
解:如图所示,
22.
【答案】
解:如图所示:
.
【解答】
解:如图所示:
.
23.
【答案】
解:(1)如图EF就是DE的投影.
(2)由作图可知AC//DF,
∴ ∠ACB=∠DFE,
∵ ∠ABC=∠DEF=90?,
∴ △ABC?△DEF.
∴ ABBC=DEEF,
即53=DE6,
DE=10.
答:DE的长为10m.
【解答】
解:(1)如图EF就是DE的投影.
(2)由作图可知AC//DF,
∴ ∠ACB=∠DFE,
∵ ∠ABC=∠DEF=90?,
∴ △ABC?△DEF.
∴ ABBC=DEEF,
即53=DE6,
DE=10.
答:DE的长为10m.
24.
【答案】
解:该几何体的形状是直四棱柱,
由三视图知,棱柱底面菱形的对角线长分别为4cm,3cm,
∴ 菱形的边长=(32)2+(42)2=52(cm),
棱柱的侧面积=52×8×4=80(cm2).
【解答】
解:该几何体的形状是直四棱柱,
由三视图知,棱柱底面菱形的对角线长分别为4cm,3cm,
∴ 菱形的边长=(32)2+(42)2=52(cm),
棱柱的侧面积=52×8×4=80(cm2).
25.
【答案】
如图所示,四边形A'B'C'D'即为所求.
【解答】
如图所示,四边形A'B'C'D'即为所求.
26.
【答案】
解:(1)当AB平行于投影面P时,它的正投影A'B'=AB=1;
(2)如图:作AC⊥BB'于点C,
则A'B'=AC=ABcos30?=32.
【解答】
解:(1)当AB平行于投影面P时,它的正投影A'B'=AB=1;
(2)如图:作AC⊥BB'于点C,
则A'B'=AC=ABcos30?=32.
(满分100分;时间:90分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 围成圆形的栏杆的影子都在圈外,则影子是在下列哪种光照射下形成的( )
A.太阳光 B.圈里的路灯的灯光
C.手电筒发出的灯光 D.台灯的灯光
?2. 如图,小强用5个相同的小立方体搭成的立体图形研究几何体的三视图的变化情况,若由图1变到图2,不改变的是( )
A.主视图 B.主视图和左视图
C.主视图和俯视图 D.左视图和俯视图
?3. 三棱柱的三视图如图,△EFG中,EF=8cm,EG=12cm,∠EGF=30?,则AB的长( )
A.6 B.8 C.12 D.33
?
4. 用若干个相同的小正方体搭成一个几何体模型,其主视图与左视图如图所示,则该几何体的俯视图不可能是(? ? ? ? )
A. B. C. D.
?
5. 如图是某几何体的三视图,其侧面积为(? ? ? ? )
A.6 B.4π C.6π D.12π
?
6. 如图是空心圆柱体在指定方向上的视图,正确的是( )
A. B. C. D.
?
7. 如图是某几何体的三视图,则该几何体的侧面积是( )
A.210π B.410π C.15π D.413π
?
8. 右图所示的正三棱柱的主视图的是( )
A. B. C. D.
?
9. 如图是一个“中”的几何体,则该几何体的俯视图为( )
A. B. C. D.
?
10. 如图,把一个棱长为3的正方体的每个面等分成9个小正方形,然后沿每个面正中心的一个正方形向里挖空(相当于挖去7个小正方体),所得到的几何体的表面积是( )
A.78 B.72 C.54 D.48
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
11. 如图是两棵小树在同一时刻的影子,那么图①是________投影,图②是________投影.
?
12. 如图是由五个大小相同的正方体搭成的几何体,从________面看所得到的性状图的面积最小. ?
13. 某几何体的三视图如图,那么该几何体是________.
14. 一个几何体的主视图,左视图,俯视图都是同一个图形,那么这个几何体形状可能是________(填写一个即可). ?
15. 同一时刻,同一地区,太阳光下物体的高度与投影长的比是________.
?
16. 已知两个电线杆在太阳光下形成两条不同的线段,那么这两条线段可能________,也可能________.
?
17. 两个物体在同一灯光下得到的影子构成的两个三角形________相似三角形.(填“是”或“不同是)
?
18. 一个正方体边长2cm,这个正方体的表面积为________cm2,体积为________cm3.
?
19. 如图,这个图形从正面看是________,从左面看是________,从上面看是________. ?
20. 长方体的主视图与左视图如图所示(单位:cm),则其俯视图的面积是________.
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
21. 分别画出图中几何体的主视图、左视图、俯视图.
?
22. 一个几何体是由若干个大小相同的正方体搭成的,如图是从这个几何体上面看所形成的图形,上面的数字表示在该位置的正方体的个数,请你画出它从正面看和从左面看的图形.
?
23. 如图1,国庆期间某广场旗杆附近搭建了一座花篮.图2为从该场景抽象出的数学模型,已知花篮高度 AB=5m ,某一时刻花篮在阳光下的投影 BC=3m.
(1)请你用尺规作图法在图2中作出此时旗杆DE在阳光下的投影EF;(不写作法,保留作图痕迹)
(2)在测量AB的投影时,同时测出DE在阳光下的投影长为6m,请你计算DE的长.
?
24. 一个几何体的三视图如图所示,它的俯视图为菱形.请写出该几何体的形状,并根据图中所给的数据求出它的侧面积.
?
25. 如图,窗户的一条边AB在地面上的平行投影为A'B'.将整个窗户的投影补充完整.
?
26. 如图,已知线段AB的长为1,投影面为P.
(1)如图1,当AB平行于投影面P时,它的正投影A'B'的长是多少?
(2)在(1)的基础上,点A不动,线段AB绕着点A在垂直于P的平面内逆时针旋转30?,如图2,这时AB的正投影A'B'将比原来缩短,试求出这时A'B'的长度.
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
B
【解答】
解:因为围成圆形的栏杆的影子都在圈外,所以光源在圈里,即影子是在下圈里的路灯的灯光照射下形成的.故选B.
2.
【答案】
D
【解答】
从上边看得到的图形都是第一层一个小正方形,第二层是三个小正方形,从左边看第一层是两个小正方形,第二层左边一个小正方形,
3.
【答案】
A
【解答】
解:过点E作EQ⊥FG于点Q,
由题意可得出:EQ=AB,
∵ EG=12cm,∠EGF=30?,
∴ EQ=AB=12×12=6(cm).
故选A.
4.
【答案】
D
【解答】
解:根据主视图、左视图,可知A,B,C中的图形均有可能是几何体的俯视图,只有D中的图形不可能是几何体的俯视图.
故选D.
5.
【答案】
C
【解答】
解:观察三视图知:该几何体为圆柱,高为3cm,底面直径为2cm,
∴ 侧面积为:πdh=2π×3=6π.
故选C.
6.
【答案】
C
【解答】
解:圆柱的主视图是矩形,里面有两条用虚线表示的看不到的棱,故选C.
7.
【答案】
B
【解答】
解:由图可得,该几何体为一个圆锥,
根据圆锥的侧面积公式可得πrl=π×2×62+22=410π.
故选B.
8.
【答案】
B
【解答】
解:从正面看三棱柱,是矩形里面一条虚线.故选B.
9.
【答案】
C
【解答】
解:从上边看是由5个矩形组成得,左边矩形的右边是虚线,右边矩形的左边是虚线,
故选:C.
10.
【答案】
B
【解答】
解:如图所示,周边的六个挖空的正方体每个面增加4个正方形,且减少了1个正方形,则每个面的正方形个数为12个,则表面积为12×6×1=72.
故选B.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
平行,中心
【解答】
解:图①是平行投影;
图②是中心投影.
故答案为:平行、中心.
12.
【答案】
左
【解答】
解:从正面看第一层是三个小正方形,第二层左边一个小正方形,共四个小正方形;
从上面看第一层左边一个小正方形,第二层是三个小正方形,共四个小正方形;
从左面看第一层两个小正方形,第二层左边一个小正方形,共三个小正方形,
故答案为:左.
13.
【答案】
圆柱
【解答】
解:∵ 几何体的主视图和俯视图都是宽度相等的长方形,
故该几何体是一个柱体,
又∵ 俯视图是一个圆,
故该几何体是一个圆柱
故答案为:圆柱.
14.
【答案】
正方体或球体(填一个即可)
【解答】
解:依题意,主视图、左视图以及俯视图都相同的几何体是正方体或球体.
15.
【答案】
成正比例的
【解答】
解:同一时刻,同一地区,太阳光下物体的高度与投影长的比是成正比例的.
16.
【答案】
平行,在同一直线上
【解答】
解:当两个电线杆在同一条直线上时,所形成的两条不同的线段在同一直线上,
当两个电线杆不在同一条直线上时,所形成的两条不同的线段平行,
故答案为:平行或在同一直线上.
17.
【答案】
不是
【解答】
解:要使立于地面上的不同的物体与影子构成的三角形相似,必须是平行投影,而灯光是中心投影,所以两个物体在同一灯光下得到的影子构成的两个三角形不是相似三角形.
故答案为:不是.
18.
【答案】
24,8
【解答】
解:2×2×6=24(平方厘米);
2×2×2=8(立方厘米);
答:这个正方体的表面积是24平方厘米,体积是8立方厘米.
故答案为:24,8.
19.
【答案】
梯形,梯形,同心圆环
【解答】
解:该图形从正面看是?梯形,从左面看是梯形,从上面看是同心圆环.
故答案为:梯形,梯形,同心圆环.
20.
【答案】
12(cm2)
【解答】
解:根据题意,正方体的俯视图是矩形,它的长是4cm,宽是3cm,面积=4×3=12(cm2),
故答案为:12(cm2).
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
解:如图所示,
【解答】
解:如图所示,
22.
【答案】
解:如图所示:
.
【解答】
解:如图所示:
.
23.
【答案】
解:(1)如图EF就是DE的投影.
(2)由作图可知AC//DF,
∴ ∠ACB=∠DFE,
∵ ∠ABC=∠DEF=90?,
∴ △ABC?△DEF.
∴ ABBC=DEEF,
即53=DE6,
DE=10.
答:DE的长为10m.
【解答】
解:(1)如图EF就是DE的投影.
(2)由作图可知AC//DF,
∴ ∠ACB=∠DFE,
∵ ∠ABC=∠DEF=90?,
∴ △ABC?△DEF.
∴ ABBC=DEEF,
即53=DE6,
DE=10.
答:DE的长为10m.
24.
【答案】
解:该几何体的形状是直四棱柱,
由三视图知,棱柱底面菱形的对角线长分别为4cm,3cm,
∴ 菱形的边长=(32)2+(42)2=52(cm),
棱柱的侧面积=52×8×4=80(cm2).
【解答】
解:该几何体的形状是直四棱柱,
由三视图知,棱柱底面菱形的对角线长分别为4cm,3cm,
∴ 菱形的边长=(32)2+(42)2=52(cm),
棱柱的侧面积=52×8×4=80(cm2).
25.
【答案】
如图所示,四边形A'B'C'D'即为所求.
【解答】
如图所示,四边形A'B'C'D'即为所求.
26.
【答案】
解:(1)当AB平行于投影面P时,它的正投影A'B'=AB=1;
(2)如图:作AC⊥BB'于点C,
则A'B'=AC=ABcos30?=32.
【解答】
解:(1)当AB平行于投影面P时,它的正投影A'B'=AB=1;
(2)如图:作AC⊥BB'于点C,
则A'B'=AC=ABcos30?=32.
