人教版数学九年级下册 第28章 28.2解直角三角形及其应用同步测试试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学九年级下册 第28章 28.2解直角三角形及其应用同步测试试题(一)(Word版 含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 487.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 15:05:15 | ||
图片预览

文档简介
解直角三角形及其应用同步测试试题(一)
一.选择题
1.如图,一艘快艇从O港出发,向西北方向行驶到M处,然后向正东行驶到N处,再向西南方向行驶,共经过1.5小时回到O港,已知快艇的速度是每小时50海里,则M,N之间的距离是( )海里
A.75﹣75 B. C.75 D.50
2.如图,小刚家在甲楼,他想利用最近所学知识测量对面的乙楼的高度,小刚在甲楼楼底B点测得乙楼楼顶C点的仰角为45°,当他爬上楼顶,在A点处测得乙楼D点的仰角为30°.若AB=10m,CD=6m,则乙楼的高度CE为( )m.(参考数据:≈1.41,≈1.73,精确到0.1m.)
A.21.8 B.37.6 C.37.8 D.38.2
3.小明同学想要测量如图所示的仙女峰的高度,他利用已学的数学知识设计了一个实践方案,并实施了如下操作:先在水平地面A处测得山顶B的仰角∠BAC为38.7°,再由A沿水平方向前进377米到达山脚C处,测得山坡BC的坡度为1:0.6,那么仙女峰的高度为( )(参考数据:tan38.7°≈0.8)
A.650 米 B.580 米 C.540 米 D.520 米
4.如图所示,河堤横断面迎水坡AB的坡度是1:2,堤高BC=4m,则坡面AB的长度是( )
A.8m B.16m C.4m D.4m
5.如图,河堤横断面迎水坡AB的坡比是1:,堤高BC=2米,则迎水坡宽度AC的长为( )
A.4米 B.2米 C.米 D.2米
6.如图,从A处观测铁塔顶部的仰角是30°,向前走30米到达B处,观测铁塔的顶部的仰角是45°,则铁塔高度是( )米
A.15+1 B. C. D.15+15
7.某同学利用数学知识测量建筑物DEFG的高度.他从点A出发沿着坡度为i=1:2.4的斜坡AB步行26米到达点B处,用测角仪测得建筑物顶端D的仰角为37°,建筑物底端E的俯角为30°.若AF为水平的地面,侧角仪竖直放置,其高度BC=1.6米,则此建筑物的高度DE约为(精确到0.1米,参考数据:≈1.73,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)( )
A.23.0米 B.23.6米 C.26.7米 D.28.9米
8.如图,一个坡角为15°的看台横截面上有旗杆CD,在这横截面上进行测量得到以下数据:在点A和点B处测得旗杆顶端的仰角分别为60°和30°,点A离地面高度为1米,且测得点A到点B的距离为8米,则旗杆的高度为( )
A.23米 B.24米 C.25米 D.26米
9.如图,某停车场入口的栏杆AB,从水平位置绕点O旋转到A′B′的位置,已知AO的长为4米.若栏杆的旋转角∠AOA′=α,则栏杆A端升高的高度为( )
A.米 B.4sinα米 C.米 D.4cosα米
10.2020年3月20日,深圳市民中心及周边楼宇为当日返回深圳的援鄂医疗队员亮灯,欢迎最美逆行者回家.小洪在欢迎英雄回家现场,如图,若他观测到英雄画像电子屏顶端A和底端C的仰角分别为∠α和∠β,小洪所站位置E到电子屏边缘AC垂直地面的B点距离为m米,那么英雄画像电子屏高AC为( )
A.(﹣)米 B.mtan(α﹣β)米
C.m(tanα﹣tanβ)米 D.米
二.填空题
11.已知某斜坡的坡度i=1:3,当铅垂高度为3米时,水平宽度为 米.
12.在△ABC中,sinB=,tanC=,AB=3,则AC的长为 .
13.如图,在△ABD中,点C为BD边中点,连接AC,点E在AC上,连接BE,若AB=AC,tan∠BAC=,∠BAC=2∠EBC,BC=,则AD的长为 .
14.如图,△ABC的顶点都是正方形网格中的格点,则cosA的值为 .
15.如图,某堤坝的坝高为12米,如果迎水坡的坡度为1:0.75,那么该大坝迎水坡AB的长度为 米.
三.解答题
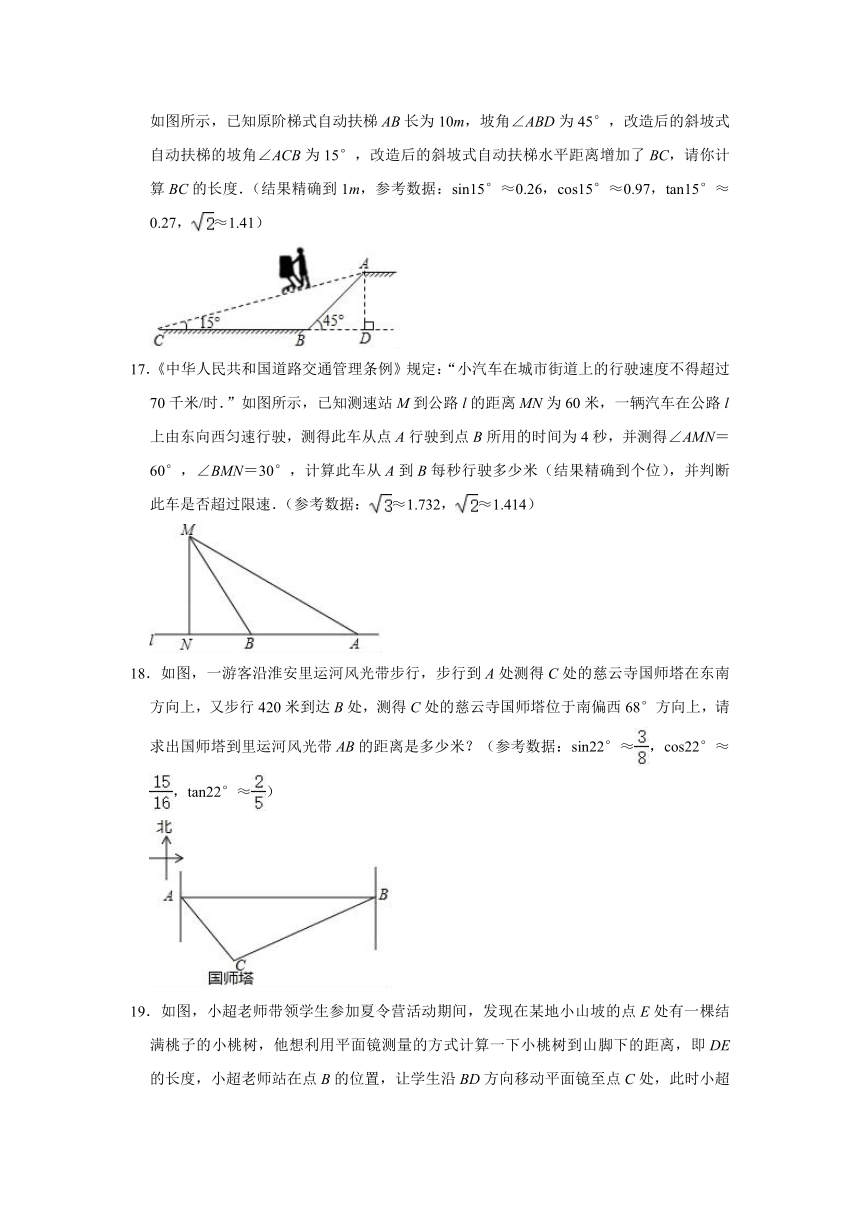
16.淮安华联商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯,如图所示,已知原阶梯式自动扶梯AB长为10m,坡角∠ABD为45°,改造后的斜坡式自动扶梯的坡角∠ACB为15°,改造后的斜坡式自动扶梯水平距离增加了BC,请你计算BC的长度.(结果精确到1m,参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,≈1.41)
17.《中华人民共和国道路交通管理条例》规定:“小汽车在城市街道上的行驶速度不得超过70千米/时.”如图所示,已知测速站M到公路l的距离MN为60米,一辆汽车在公路l上由东向西匀速行驶,测得此车从点A行驶到点B所用的时间为4秒,并测得∠AMN=60°,∠BMN=30°,计算此车从A到B每秒行驶多少米(结果精确到个位),并判断此车是否超过限速.(参考数据:≈1.732,≈1.414)
18.如图,一游客沿淮安里运河风光带步行,步行到A处测得C处的慈云寺国师塔在东南方向上,又步行420米到达B处,测得C处的慈云寺国师塔位于南偏西68°方向上,请求出国师塔到里运河风光带AB的距离是多少米?(参考数据:sin22°≈,cos22°≈,tan22°≈)
19.如图,小超老师带领学生参加夏令营活动期间,发现在某地小山坡的点E处有一棵结满桃子的小桃树,他想利用平面镜测量的方式计算一下小桃树到山脚下的距离,即DE的长度,小超老师站在点B的位置,让学生沿BD方向移动平面镜至点C处,此时小超老师在平面镜内可以看到点E,且BC=2.7米,CD=11.5米,∠CDE=120°,已知小超老师的身高为1.8米,请你利用以上的数据求出DE的长度.(结果精确到1米,≈1.7)
20.无影塔位于河南汝南城南,俗传冬至正午无塔影,故称无影塔;相传为唐代和尚悟颖所建,故又称“悟颖塔”,该塔应建于北宋中、早期,为豫南地区现存最古老砖塔某数学小组为了度量塔高进行了如下操作:用一架无人机在距离塔基(B)某处垂直起飞30米至点C处,测得塔基B处的俯角为75°,将无人机沿水平方向向右飞行8.6米至点D,在此处测得塔顶A的俯角为30°,请依据题中数据计算无影塔的高度.(结果精确到1cm,参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73,≈1.73)
参考答案与试题解析
一.选择题
1.【解答】解:如图所示:
由题意得:∠NOC=45°,∠MOD=45°,
∴∠MON=90°,
∵MN∥x轴,
∴∠MNO=∠NOC=45°,∠NMO=∠MOD=45°,
∴△MON为等腰直角三角形,
∴OM=ON=MN,
∵OM+OM+MN=50×1.5=75(海里),
∴MN+MN+MN=75,
解得:MN=75﹣75(海里),
即M,N之间的距离是(75﹣75)海里;
故选:A.
2.【解答】解:如图,过点A作AF⊥CE于点F,
根据题意可知:
AB⊥BE,CE⊥BE,
∴四边形ABEF是矩形,
∴AF=BE,EF=AB=10,
在Rt△CBE中,∠CBE=45,
∴BE=CE=CD+DF+FE=6+DF+10=16+DF,
在Rt△ADF中,∠DAF=30°,
∴DF=AFtan30°,
∴DF=(16+DF)×,
解得DF=8(+1),
∴CE=16+DF=24+8≈37.8(m).
答:乙楼的高度CE为37.8m.
故选:C.
3.【解答】解:如图,过点B作BD⊥AC于点D,
∵山坡BC的坡度为1:0.6,
∴,
则CD=0.6BD.
∵∠BAC为38.7°,
∴tan38.7°=.
∵AC=377米,tan38.7°≈0.8,
∴≈0.8,
解得BD=580(米).
答:仙女峰的高度约为580米,
故选:B.
4.【解答】解:Rt△ABC中,BC=4m,tanA=1:2;
∴AC==8m,
∴AB===4(m).
故选:C.
5.【解答】解:迎水坡AB的坡比是1:,即tan∠A=,
则,
又∵BC=2米,
∴AC=BC=2(米).
故选:B.
6.【解答】解:设铁塔的高度为x米,
在Rt△BCD中,
∵∠DBC=45°,
∴BC=CD=x,
在Rt△ACD中,
∵∠DAC=30°,
∴=tan30°=,
∴AC=x,
∵AB=30米,
∴x﹣x=30,
解得:x=15(+1)米,
即铁塔的高度为15(+1)米,
故选:D.
7.【解答】解:如图所示:过点B作BN⊥AE,CM⊥DE垂足分别为:N,M,
∵i=1:2.4,AB=26m,
∴设BN=x,则AN=2.4x,
∴AB=2.6x,
则2.6x=26,
解得:x=10,
故BN=10,
∴CN=ME=11.6,
则tan30°===,
解得:CM=11.6,
则tan37°===0.75,
解得:DM≈15.1(m),
故DE=DM+EM=15.1+11.6=26.7(m).
故选:C.
8.【解答】解:过A作AE⊥CD于E,AF⊥BC于F,
∵∠BAC=180°﹣15°﹣60°=105°,∠ABC=45°
∴∠ACB=30°,
∵AB=8,
∴AF=BF=AB=8,
∴AC=2AF=16,
∵∠AEC=90°,∠ACE=30°,
∴CE=AC=24,
∵DE=1,
∴CD=24+1=25(米),
答:旗杆的高度为25米,
故选:C.
9.【解答】解:过点A′作A′C⊥AB于点C,
由题意可知:A′O=AO=4,
∴sinα=,
∴A′C=4sinα,
故选:B.
10.【解答】解:根据题意得,DF=BE=m米,
在Rt△ADF中,∵tanα=,
∴AD=DFtanα=mtanα,
在Rt△CDF中,∵tanβ=,
∴CD=DFtanβ=mtanβ,
∴AC=AD﹣CD=mtanα﹣mtanβ=m(tanα﹣tanβ)(米),
答:英雄画像电子屏高AC为m(tanα﹣tanβ)(米),
故选:C.
二.填空题(共5小题)
11.【解答】解:∵斜坡的坡度i==1:3,铅垂高度=3米
∴水平宽度=3×铅直高度=3×3=9(米),
故答案为:9.
12.【解答】解:过A作AD⊥BC,
在Rt△ABD中,sinB=,AB=3,
∴AD=ABsinB=1,
在Rt△ACD中,tanC=,
∴=,即CD=,
根据勾股定理得:AC===,
故答案为:.
13.【解答】解:作AF⊥BC于点F,
∵AB=AC,
∴AF平分∠BAC,BF=CF,
∴∠CAF=∠BAC,
即2∠CAF=∠BAC,
∵∠BAC=2∠EBC,
∴∠CAF=∠EBC,
∵∠CAF+∠ACF=90°,
∴∠EBC+∠ACF=90°,
∴∠BEC=90°,
∴∠AEB=90°,
∵tan∠BAC=,
∴设BE=3x,则AE=4x,
∴AB==5x,
∴AC=5x,
∴CE=x,
∵BC=,BE=3x,CE=x,
∴10=(3x)2+x2,
解得x1=1,x2=﹣1(舍去),
∴AC=5x=5,
∵∠AFC=90°,BF=BC=,
∴AF==,
∵点C为BD的中点,
∴FD=+=,
∵∠AFD﹣90°,
∴AD==3,
故答案为:3.
14.【解答】解:如图,作CH⊥AB于H,设小正方形的边长为1.则AC==,
在Rt△ACH中,cosA===,
故答案为:.
15.【解答】解:如图,过点B作BC垂直于水平面于点C,
∵BC:AC=1:0.75,
∴12:AC=1:0.75,
∴AC=9(米),
∴AB===15(米),
答:该大坝迎水坡AB的长度为15米.
故答案为:15.
三.解答题(共5小题)
16.【解答】解:在Rt△ABD中,∠ABD=45°,AB=10,
∴AD=BD=ABsin∠ABD=10×=5≈7,
∵∠ACD=15°,tan∠ACD=,
∴CD≈≈≈26,
∴BC=CD﹣BD=26﹣7=19.
故BC的长度约为19米.
17.【解答】解:在Rt△AMN中,AN=MN×tan∠AMN=MN×tan60°=60×=60(米).
在Rt△BMN中,BN=MN×tan∠BMN=MN×tan30°=60×=20(米).
∴AB=AN﹣BN=60﹣20=40(米)
则A到B的平均速度为:=10≈17(米/秒).
∵70千米/时=米/秒≈19米/秒>17米/秒,
∴此车没有超过限速.
18.【解答】解:过点C作CD⊥AB于D,如图所示:
设CD=2x,
由题意得:AB=420,∠CAD=45°,∠CBD=22°,
在Rt△ACD中,tan∠CAD==tan45°=1,
∴AD=CD=2x,
在Rt△BCD中,tan∠CBD==tan22°≈,
∴BD=5x,
∵AD+BD=AB,
∴2x+5x=420,
∴x=60,
∴CD=2x=120(米);
答:国师塔到里运河风光带AB的距离约120米.
19.【解答】解:如图,过点E作EF⊥DN于点F,
根据题意可知:
∠ACB=∠ECD,
∵∠ABC=∠EFC=90°,
∴tan∠ACB=tan∠ECD,
∴=,
∵∠CDE=120°,
∴∠EDF=60°,
设DF=x,则DE=2x,EF=x,
∴CF=CD+DF=11.5+x,
∴=,
解得x=,
∴DE=2x=≈15(米).
答:DE的长度约为15米.
20.【解答】解:过点C作CM⊥BO,垂足为M,设DC与BA的延长线交于点E,如图:
设AB为x米.
∵∠E=∠ABM=∠BMC=90°,
∴四边形EBMC为矩形,
∴MC=BE=30,
∵∠BCE=75°,tan∠BCE==3.73,
∴CE≈≈8.04,
在Rt△AED中,∠ADE=30°,AE=30﹣x,tan∠ADE==,
∴,
∵CD=DE﹣CE,
∴,
解得:x≈20.38,
答:无影塔的高度约为20.38米.
一.选择题
1.如图,一艘快艇从O港出发,向西北方向行驶到M处,然后向正东行驶到N处,再向西南方向行驶,共经过1.5小时回到O港,已知快艇的速度是每小时50海里,则M,N之间的距离是( )海里
A.75﹣75 B. C.75 D.50
2.如图,小刚家在甲楼,他想利用最近所学知识测量对面的乙楼的高度,小刚在甲楼楼底B点测得乙楼楼顶C点的仰角为45°,当他爬上楼顶,在A点处测得乙楼D点的仰角为30°.若AB=10m,CD=6m,则乙楼的高度CE为( )m.(参考数据:≈1.41,≈1.73,精确到0.1m.)
A.21.8 B.37.6 C.37.8 D.38.2
3.小明同学想要测量如图所示的仙女峰的高度,他利用已学的数学知识设计了一个实践方案,并实施了如下操作:先在水平地面A处测得山顶B的仰角∠BAC为38.7°,再由A沿水平方向前进377米到达山脚C处,测得山坡BC的坡度为1:0.6,那么仙女峰的高度为( )(参考数据:tan38.7°≈0.8)
A.650 米 B.580 米 C.540 米 D.520 米
4.如图所示,河堤横断面迎水坡AB的坡度是1:2,堤高BC=4m,则坡面AB的长度是( )
A.8m B.16m C.4m D.4m
5.如图,河堤横断面迎水坡AB的坡比是1:,堤高BC=2米,则迎水坡宽度AC的长为( )
A.4米 B.2米 C.米 D.2米
6.如图,从A处观测铁塔顶部的仰角是30°,向前走30米到达B处,观测铁塔的顶部的仰角是45°,则铁塔高度是( )米
A.15+1 B. C. D.15+15
7.某同学利用数学知识测量建筑物DEFG的高度.他从点A出发沿着坡度为i=1:2.4的斜坡AB步行26米到达点B处,用测角仪测得建筑物顶端D的仰角为37°,建筑物底端E的俯角为30°.若AF为水平的地面,侧角仪竖直放置,其高度BC=1.6米,则此建筑物的高度DE约为(精确到0.1米,参考数据:≈1.73,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)( )
A.23.0米 B.23.6米 C.26.7米 D.28.9米
8.如图,一个坡角为15°的看台横截面上有旗杆CD,在这横截面上进行测量得到以下数据:在点A和点B处测得旗杆顶端的仰角分别为60°和30°,点A离地面高度为1米,且测得点A到点B的距离为8米,则旗杆的高度为( )
A.23米 B.24米 C.25米 D.26米
9.如图,某停车场入口的栏杆AB,从水平位置绕点O旋转到A′B′的位置,已知AO的长为4米.若栏杆的旋转角∠AOA′=α,则栏杆A端升高的高度为( )
A.米 B.4sinα米 C.米 D.4cosα米
10.2020年3月20日,深圳市民中心及周边楼宇为当日返回深圳的援鄂医疗队员亮灯,欢迎最美逆行者回家.小洪在欢迎英雄回家现场,如图,若他观测到英雄画像电子屏顶端A和底端C的仰角分别为∠α和∠β,小洪所站位置E到电子屏边缘AC垂直地面的B点距离为m米,那么英雄画像电子屏高AC为( )
A.(﹣)米 B.mtan(α﹣β)米
C.m(tanα﹣tanβ)米 D.米
二.填空题
11.已知某斜坡的坡度i=1:3,当铅垂高度为3米时,水平宽度为 米.
12.在△ABC中,sinB=,tanC=,AB=3,则AC的长为 .
13.如图,在△ABD中,点C为BD边中点,连接AC,点E在AC上,连接BE,若AB=AC,tan∠BAC=,∠BAC=2∠EBC,BC=,则AD的长为 .
14.如图,△ABC的顶点都是正方形网格中的格点,则cosA的值为 .
15.如图,某堤坝的坝高为12米,如果迎水坡的坡度为1:0.75,那么该大坝迎水坡AB的长度为 米.
三.解答题
16.淮安华联商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯,如图所示,已知原阶梯式自动扶梯AB长为10m,坡角∠ABD为45°,改造后的斜坡式自动扶梯的坡角∠ACB为15°,改造后的斜坡式自动扶梯水平距离增加了BC,请你计算BC的长度.(结果精确到1m,参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,≈1.41)
17.《中华人民共和国道路交通管理条例》规定:“小汽车在城市街道上的行驶速度不得超过70千米/时.”如图所示,已知测速站M到公路l的距离MN为60米,一辆汽车在公路l上由东向西匀速行驶,测得此车从点A行驶到点B所用的时间为4秒,并测得∠AMN=60°,∠BMN=30°,计算此车从A到B每秒行驶多少米(结果精确到个位),并判断此车是否超过限速.(参考数据:≈1.732,≈1.414)
18.如图,一游客沿淮安里运河风光带步行,步行到A处测得C处的慈云寺国师塔在东南方向上,又步行420米到达B处,测得C处的慈云寺国师塔位于南偏西68°方向上,请求出国师塔到里运河风光带AB的距离是多少米?(参考数据:sin22°≈,cos22°≈,tan22°≈)
19.如图,小超老师带领学生参加夏令营活动期间,发现在某地小山坡的点E处有一棵结满桃子的小桃树,他想利用平面镜测量的方式计算一下小桃树到山脚下的距离,即DE的长度,小超老师站在点B的位置,让学生沿BD方向移动平面镜至点C处,此时小超老师在平面镜内可以看到点E,且BC=2.7米,CD=11.5米,∠CDE=120°,已知小超老师的身高为1.8米,请你利用以上的数据求出DE的长度.(结果精确到1米,≈1.7)
20.无影塔位于河南汝南城南,俗传冬至正午无塔影,故称无影塔;相传为唐代和尚悟颖所建,故又称“悟颖塔”,该塔应建于北宋中、早期,为豫南地区现存最古老砖塔某数学小组为了度量塔高进行了如下操作:用一架无人机在距离塔基(B)某处垂直起飞30米至点C处,测得塔基B处的俯角为75°,将无人机沿水平方向向右飞行8.6米至点D,在此处测得塔顶A的俯角为30°,请依据题中数据计算无影塔的高度.(结果精确到1cm,参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73,≈1.73)
参考答案与试题解析
一.选择题
1.【解答】解:如图所示:
由题意得:∠NOC=45°,∠MOD=45°,
∴∠MON=90°,
∵MN∥x轴,
∴∠MNO=∠NOC=45°,∠NMO=∠MOD=45°,
∴△MON为等腰直角三角形,
∴OM=ON=MN,
∵OM+OM+MN=50×1.5=75(海里),
∴MN+MN+MN=75,
解得:MN=75﹣75(海里),
即M,N之间的距离是(75﹣75)海里;
故选:A.
2.【解答】解:如图,过点A作AF⊥CE于点F,
根据题意可知:
AB⊥BE,CE⊥BE,
∴四边形ABEF是矩形,
∴AF=BE,EF=AB=10,
在Rt△CBE中,∠CBE=45,
∴BE=CE=CD+DF+FE=6+DF+10=16+DF,
在Rt△ADF中,∠DAF=30°,
∴DF=AFtan30°,
∴DF=(16+DF)×,
解得DF=8(+1),
∴CE=16+DF=24+8≈37.8(m).
答:乙楼的高度CE为37.8m.
故选:C.
3.【解答】解:如图,过点B作BD⊥AC于点D,
∵山坡BC的坡度为1:0.6,
∴,
则CD=0.6BD.
∵∠BAC为38.7°,
∴tan38.7°=.
∵AC=377米,tan38.7°≈0.8,
∴≈0.8,
解得BD=580(米).
答:仙女峰的高度约为580米,
故选:B.
4.【解答】解:Rt△ABC中,BC=4m,tanA=1:2;
∴AC==8m,
∴AB===4(m).
故选:C.
5.【解答】解:迎水坡AB的坡比是1:,即tan∠A=,
则,
又∵BC=2米,
∴AC=BC=2(米).
故选:B.
6.【解答】解:设铁塔的高度为x米,
在Rt△BCD中,
∵∠DBC=45°,
∴BC=CD=x,
在Rt△ACD中,
∵∠DAC=30°,
∴=tan30°=,
∴AC=x,
∵AB=30米,
∴x﹣x=30,
解得:x=15(+1)米,
即铁塔的高度为15(+1)米,
故选:D.
7.【解答】解:如图所示:过点B作BN⊥AE,CM⊥DE垂足分别为:N,M,
∵i=1:2.4,AB=26m,
∴设BN=x,则AN=2.4x,
∴AB=2.6x,
则2.6x=26,
解得:x=10,
故BN=10,
∴CN=ME=11.6,
则tan30°===,
解得:CM=11.6,
则tan37°===0.75,
解得:DM≈15.1(m),
故DE=DM+EM=15.1+11.6=26.7(m).
故选:C.
8.【解答】解:过A作AE⊥CD于E,AF⊥BC于F,
∵∠BAC=180°﹣15°﹣60°=105°,∠ABC=45°
∴∠ACB=30°,
∵AB=8,
∴AF=BF=AB=8,
∴AC=2AF=16,
∵∠AEC=90°,∠ACE=30°,
∴CE=AC=24,
∵DE=1,
∴CD=24+1=25(米),
答:旗杆的高度为25米,
故选:C.
9.【解答】解:过点A′作A′C⊥AB于点C,
由题意可知:A′O=AO=4,
∴sinα=,
∴A′C=4sinα,
故选:B.
10.【解答】解:根据题意得,DF=BE=m米,
在Rt△ADF中,∵tanα=,
∴AD=DFtanα=mtanα,
在Rt△CDF中,∵tanβ=,
∴CD=DFtanβ=mtanβ,
∴AC=AD﹣CD=mtanα﹣mtanβ=m(tanα﹣tanβ)(米),
答:英雄画像电子屏高AC为m(tanα﹣tanβ)(米),
故选:C.
二.填空题(共5小题)
11.【解答】解:∵斜坡的坡度i==1:3,铅垂高度=3米
∴水平宽度=3×铅直高度=3×3=9(米),
故答案为:9.
12.【解答】解:过A作AD⊥BC,
在Rt△ABD中,sinB=,AB=3,
∴AD=ABsinB=1,
在Rt△ACD中,tanC=,
∴=,即CD=,
根据勾股定理得:AC===,
故答案为:.
13.【解答】解:作AF⊥BC于点F,
∵AB=AC,
∴AF平分∠BAC,BF=CF,
∴∠CAF=∠BAC,
即2∠CAF=∠BAC,
∵∠BAC=2∠EBC,
∴∠CAF=∠EBC,
∵∠CAF+∠ACF=90°,
∴∠EBC+∠ACF=90°,
∴∠BEC=90°,
∴∠AEB=90°,
∵tan∠BAC=,
∴设BE=3x,则AE=4x,
∴AB==5x,
∴AC=5x,
∴CE=x,
∵BC=,BE=3x,CE=x,
∴10=(3x)2+x2,
解得x1=1,x2=﹣1(舍去),
∴AC=5x=5,
∵∠AFC=90°,BF=BC=,
∴AF==,
∵点C为BD的中点,
∴FD=+=,
∵∠AFD﹣90°,
∴AD==3,
故答案为:3.
14.【解答】解:如图,作CH⊥AB于H,设小正方形的边长为1.则AC==,
在Rt△ACH中,cosA===,
故答案为:.
15.【解答】解:如图,过点B作BC垂直于水平面于点C,
∵BC:AC=1:0.75,
∴12:AC=1:0.75,
∴AC=9(米),
∴AB===15(米),
答:该大坝迎水坡AB的长度为15米.
故答案为:15.
三.解答题(共5小题)
16.【解答】解:在Rt△ABD中,∠ABD=45°,AB=10,
∴AD=BD=ABsin∠ABD=10×=5≈7,
∵∠ACD=15°,tan∠ACD=,
∴CD≈≈≈26,
∴BC=CD﹣BD=26﹣7=19.
故BC的长度约为19米.
17.【解答】解:在Rt△AMN中,AN=MN×tan∠AMN=MN×tan60°=60×=60(米).
在Rt△BMN中,BN=MN×tan∠BMN=MN×tan30°=60×=20(米).
∴AB=AN﹣BN=60﹣20=40(米)
则A到B的平均速度为:=10≈17(米/秒).
∵70千米/时=米/秒≈19米/秒>17米/秒,
∴此车没有超过限速.
18.【解答】解:过点C作CD⊥AB于D,如图所示:
设CD=2x,
由题意得:AB=420,∠CAD=45°,∠CBD=22°,
在Rt△ACD中,tan∠CAD==tan45°=1,
∴AD=CD=2x,
在Rt△BCD中,tan∠CBD==tan22°≈,
∴BD=5x,
∵AD+BD=AB,
∴2x+5x=420,
∴x=60,
∴CD=2x=120(米);
答:国师塔到里运河风光带AB的距离约120米.
19.【解答】解:如图,过点E作EF⊥DN于点F,
根据题意可知:
∠ACB=∠ECD,
∵∠ABC=∠EFC=90°,
∴tan∠ACB=tan∠ECD,
∴=,
∵∠CDE=120°,
∴∠EDF=60°,
设DF=x,则DE=2x,EF=x,
∴CF=CD+DF=11.5+x,
∴=,
解得x=,
∴DE=2x=≈15(米).
答:DE的长度约为15米.
20.【解答】解:过点C作CM⊥BO,垂足为M,设DC与BA的延长线交于点E,如图:
设AB为x米.
∵∠E=∠ABM=∠BMC=90°,
∴四边形EBMC为矩形,
∴MC=BE=30,
∵∠BCE=75°,tan∠BCE==3.73,
∴CE≈≈8.04,
在Rt△AED中,∠ADE=30°,AE=30﹣x,tan∠ADE==,
∴,
∵CD=DE﹣CE,
∴,
解得:x≈20.38,
答:无影塔的高度约为20.38米.
