人教版数学九年级下册 第29章 投影与视图单元测试试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学九年级下册 第29章 投影与视图单元测试试题(一)(Word版 含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 226.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 00:00:00 | ||
图片预览

文档简介
投影与视图单元测试试题(一)
一.选择题
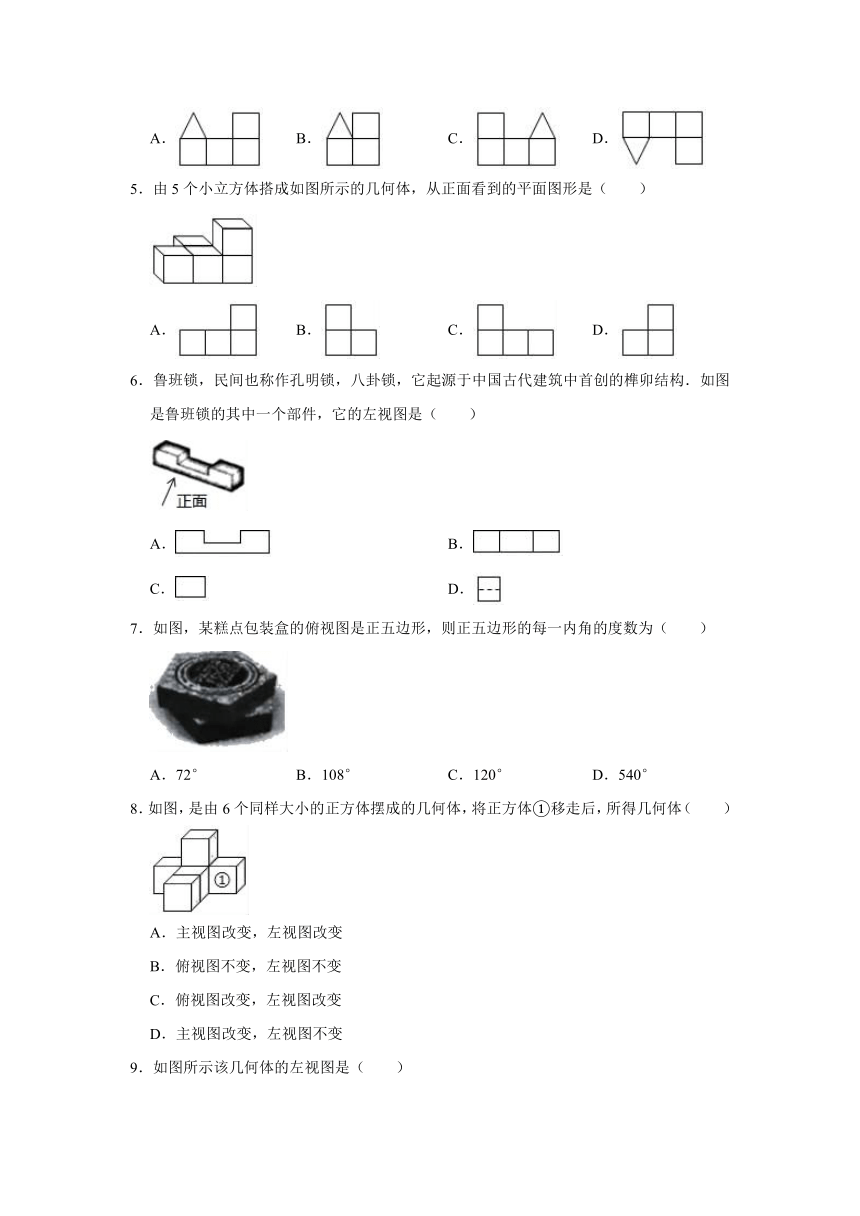
1.下列四个立体图形中,从正面和左面看到的形状图有可能不同的是( )
A. B.
C. D.
2.如图所示,由7个相同的小正方体组合成一个立体图形,从它上面看到的平面图形是( )
A. B. C. D.
3.如图是一个机器的零件,则下列说法正确的是( )
A.主视图与左视图相同
B.主视图与俯视图相同
C.左视图与俯视图相同
D.主视图、左视图与俯视图均不相同
4.如图是一个由5个小正方体和1个圆锥组成的立体图形,这个立体图形的主视图是( )
A. B. C. D.
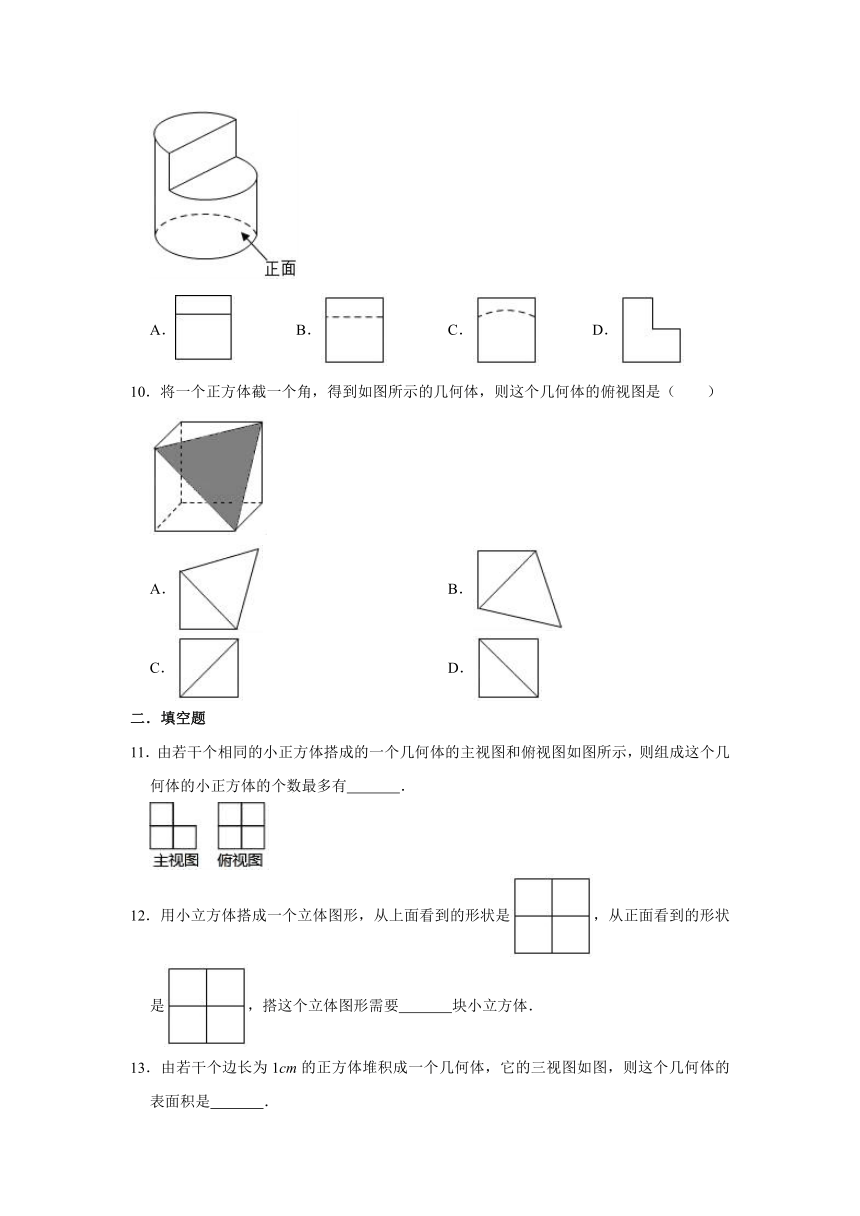
5.由5个小立方体搭成如图所示的几何体,从正面看到的平面图形是( )
A. B. C. D.
6.鲁班锁,民间也称作孔明锁,八卦锁,它起源于中国古代建筑中首创的榫卯结构.如图是鲁班锁的其中一个部件,它的左视图是( )
A. B.
C. D.
7.如图,某糕点包装盒的俯视图是正五边形,则正五边形的每一内角的度数为( )
A.72° B.108° C.120° D.540°
8.如图,是由6个同样大小的正方体摆成的几何体,将正方体①移走后,所得几何体( )
A.主视图改变,左视图改变
B.俯视图不变,左视图不变
C.俯视图改变,左视图改变
D.主视图改变,左视图不变
9.如图所示该几何体的左视图是( )
A. B. C. D.
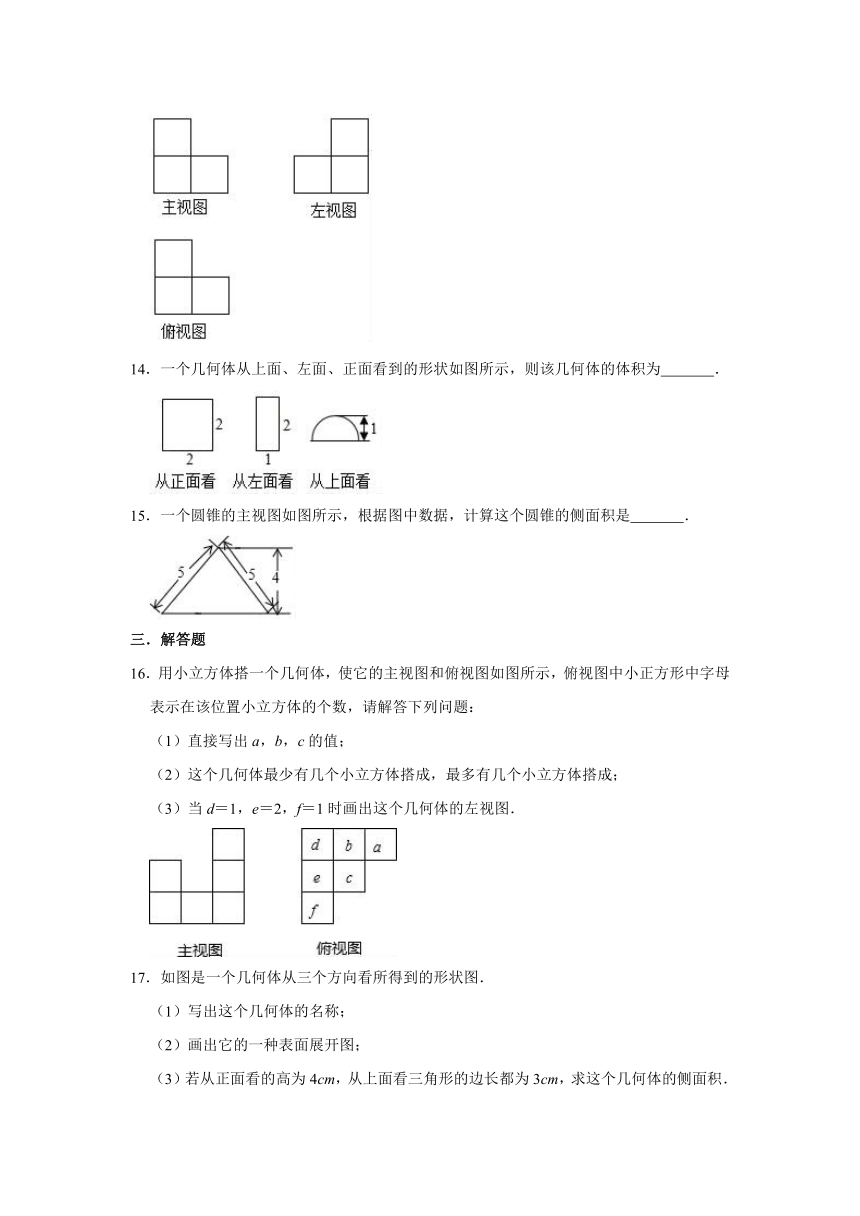
10.将一个正方体截一个角,得到如图所示的几何体,则这个几何体的俯视图是( )
A. B.
C. D.
二.填空题
11.由若干个相同的小正方体搭成的一个几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数最多有 .
12.用小立方体搭成一个立体图形,从上面看到的形状是,从正面看到的形状是,搭这个立体图形需要 块小立方体.
13.由若干个边长为1cm的正方体堆积成一个几何体,它的三视图如图,则这个几何体的表面积是 .
14.一个几何体从上面、左面、正面看到的形状如图所示,则该几何体的体积为 .
15.一个圆锥的主视图如图所示,根据图中数据,计算这个圆锥的侧面积是 .
三.解答题
16.用小立方体搭一个几何体,使它的主视图和俯视图如图所示,俯视图中小正方形中字母表示在该位置小立方体的个数,请解答下列问题:
(1)直接写出a,b,c的值;
(2)这个几何体最少有几个小立方体搭成,最多有几个小立方体搭成;
(3)当d=1,e=2,f=1时画出这个几何体的左视图.
17.如图是一个几何体从三个方向看所得到的形状图.
(1)写出这个几何体的名称;
(2)画出它的一种表面展开图;
(3)若从正面看的高为4cm,从上面看三角形的边长都为3cm,求这个几何体的侧面积.
18.用5个棱长为1的正方体,组成如图所示的几何体.
(1)该几何体的体积是 立方单位;
(2)请在所给的方格纸中,用实线画出它的三个视图.
19.双十一购物狂欢节,天猫“某玩具旗舰店”对乐高积木系列玩具将推出买一送一活动.根据积木数量的不同,厂家会订制不同型号的外包装盒.所有外包装盒均为双层上盖的长方体纸箱(上盖纸板面积刚好等于底面面积的2倍,如图1).长方体纸箱的长为a厘米,宽为b厘米,高为c厘米.
(1)请用含有a,b,c的代数式表示制作长方体纸箱需要 平方厘米纸板;
(2)如图2为若干包装好的同一型号玩具堆成几何体的三视图,则组成这个几何体的玩具个数最少为 个;
(3)由于旗舰店在双十一期间推出买一送一的活动,现要将两个同一型号的乐高积木包装在同一个大长方体的外包装盒内(如图1),已知单个乐高积木的长方体纸盒长和高相等,且宽小于长.如图3所示,现有甲,乙两种摆放方式,请分别计算甲,乙两种摆放方式所需外包装盒的纸板面积(包装盒上盖朝上),并比较哪一种方式所需纸板面积更少,说明理由.
参考答案与试题解析
一.选择题
1.【解答】解:A、从正面看到的是矩形,从左面看到的是正方形,故本选项符合题意;
B、从正面看到的是三角形,从左面看到的是三角形,故本选项不合题意;
C、从正面看到的是圆,从左面看到的是圆,故本选项不合题意;
D、从正面看到的是矩形,从左面看到的是矩形,故本选项不合题意;
故选:A.
2.【解答】解:从上面看:共分3列,从左往右分别有2,2,1个小正方形.
故选:A.
3.【解答】解:该几何体的主视图与左视图相同,底层是一个矩形,上层的中间是一个矩形;俯视图是两个同心圆.
故选:A.
4.【解答】解:从正面看易得第一层有3个正方形,第二层最左边有一个正方形,右边是一个三角形.
故选:C.
5.【解答】解:从正面看,底层是三个小正方形,上层的右边是一个小正方形.
故选:A.
6.【解答】解:从左边看,是一个矩形,矩形的中间有一条横向的虚线.
故选:D.
7.【解答】解:∵正多边形的内角和公式为:(n﹣2)×180°,
∴正五边形的内角和是:(5﹣2)×180°=540°,
则每个内角是:540°÷5=108°.
故选:B.
8.【解答】解:将正方体①移走前的主视图正方形的个数为1,2,1;正方体①移走后的主视图正方形的个数为1,2;主视图发生改变.
将正方体①移走前的左视图正方形的个数为2,1,1;正方体①移走后的左视图正方形的个数为2,1,1;左视图没有发生改变.
将正方体①移走前的俯视图正方形的个数为1,3,1;正方体①移走后的俯视图正方形的个数,1,3;俯视图发生改变.
故选:D.
9.【解答】解:从左边看的图形为:
故选:D.
10.【解答】解:从上面看可得到一个正方形,正方形里面有一条撇向的实线.
故选:C.
二.填空题(共5小题)
11.【解答】解:由俯视图易得最底层有4个小正方体,第二层最多有2个小正方体,那么搭成这个几何体的小正方体最多为4+2=6个.
故答案为:6
12.【解答】解:最下面一层有4块,
上面一层最少有2块,最多有4块,
故搭这个立体图形需要6或7或8块小立方体.
故答案为:6或7或8.
13.【解答】解:综合三视图,我们可以得出,这个几何模型的底层有2+1=3个小正方体,第二层应该有1个小正方体,
因此搭成这个几何体模型所用的小正方体的个数是3+1=4个.
所以表面积为3×6=18cm2.
故答案为:18cm2.
14.【解答】解:观察三视图可知,这个立体图形想底面为半圆的半个圆柱(如图所示).
V=π12×2=π,
故答案为π.
15.【解答】解:由勾股定理可得:底面圆的半径==3,则底面周长=6π,
由图得,母线长=5,
侧面面积=×6π×5=15π.
故选:15π.
三.解答题(共4小题)
16.【解答】解:(1)由主视图可得,俯视图中最右边一正方形处有3个小立方体,中间一列两个正方形处各有1个小立方体,
则a=3,b=1,c=1;
(2)若d,e,f处,有一处为2个小立方体,其余两处各有1个小立方体,则该几何体最少有9个小立方体搭成;
若d,e,f处,各有2个小立方体,则该几何体最多有11个小立方体搭成;
(3)当d=1,e=2,f=1时,几何体的左视图为:
.
17.【解答】解:(1)几何体的名称是三棱柱;
(2)表面展开图为:
(3)3×4×3=36cm2,
∴这个几何体的侧面积为36 cm2.
18.【解答】解:(1)几何体的体积:1×1×1×5=5(立方单位).
故该几何体的体积是5立方单位;
(2)如图所示:
故答案为:5.
19.【解答】解:(1)制作长方体纸箱需要(2ac+2bc+3ab)平方厘米纸板;
故答案为:(2ac+2bc+3ab);
(2)根据三视图知,则组成这个几何体的玩具个数最少的分布情况如下图所示:
所以组成这个几何体的玩具个数最少为9个,
故答案为:9;
(3)如图3,由题意得:a=c,a>b,
甲:2(ac+2bc+2ab)+2ab,
乙:2(2ab+2ac+bc)+2ab,
∵a>b,
∴ac>bc,
∴ac﹣bc>0,
∵甲所需纸板面积﹣乙所需纸板面积=2(ac+2bc﹣2ac﹣bc)=2(bc﹣ac)<0,
∴甲种摆放方式所需外包装盒的纸板面积更少.
一.选择题
1.下列四个立体图形中,从正面和左面看到的形状图有可能不同的是( )
A. B.
C. D.
2.如图所示,由7个相同的小正方体组合成一个立体图形,从它上面看到的平面图形是( )
A. B. C. D.
3.如图是一个机器的零件,则下列说法正确的是( )
A.主视图与左视图相同
B.主视图与俯视图相同
C.左视图与俯视图相同
D.主视图、左视图与俯视图均不相同
4.如图是一个由5个小正方体和1个圆锥组成的立体图形,这个立体图形的主视图是( )
A. B. C. D.
5.由5个小立方体搭成如图所示的几何体,从正面看到的平面图形是( )
A. B. C. D.
6.鲁班锁,民间也称作孔明锁,八卦锁,它起源于中国古代建筑中首创的榫卯结构.如图是鲁班锁的其中一个部件,它的左视图是( )
A. B.
C. D.
7.如图,某糕点包装盒的俯视图是正五边形,则正五边形的每一内角的度数为( )
A.72° B.108° C.120° D.540°
8.如图,是由6个同样大小的正方体摆成的几何体,将正方体①移走后,所得几何体( )
A.主视图改变,左视图改变
B.俯视图不变,左视图不变
C.俯视图改变,左视图改变
D.主视图改变,左视图不变
9.如图所示该几何体的左视图是( )
A. B. C. D.
10.将一个正方体截一个角,得到如图所示的几何体,则这个几何体的俯视图是( )
A. B.
C. D.
二.填空题
11.由若干个相同的小正方体搭成的一个几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数最多有 .
12.用小立方体搭成一个立体图形,从上面看到的形状是,从正面看到的形状是,搭这个立体图形需要 块小立方体.
13.由若干个边长为1cm的正方体堆积成一个几何体,它的三视图如图,则这个几何体的表面积是 .
14.一个几何体从上面、左面、正面看到的形状如图所示,则该几何体的体积为 .
15.一个圆锥的主视图如图所示,根据图中数据,计算这个圆锥的侧面积是 .
三.解答题
16.用小立方体搭一个几何体,使它的主视图和俯视图如图所示,俯视图中小正方形中字母表示在该位置小立方体的个数,请解答下列问题:
(1)直接写出a,b,c的值;
(2)这个几何体最少有几个小立方体搭成,最多有几个小立方体搭成;
(3)当d=1,e=2,f=1时画出这个几何体的左视图.
17.如图是一个几何体从三个方向看所得到的形状图.
(1)写出这个几何体的名称;
(2)画出它的一种表面展开图;
(3)若从正面看的高为4cm,从上面看三角形的边长都为3cm,求这个几何体的侧面积.
18.用5个棱长为1的正方体,组成如图所示的几何体.
(1)该几何体的体积是 立方单位;
(2)请在所给的方格纸中,用实线画出它的三个视图.
19.双十一购物狂欢节,天猫“某玩具旗舰店”对乐高积木系列玩具将推出买一送一活动.根据积木数量的不同,厂家会订制不同型号的外包装盒.所有外包装盒均为双层上盖的长方体纸箱(上盖纸板面积刚好等于底面面积的2倍,如图1).长方体纸箱的长为a厘米,宽为b厘米,高为c厘米.
(1)请用含有a,b,c的代数式表示制作长方体纸箱需要 平方厘米纸板;
(2)如图2为若干包装好的同一型号玩具堆成几何体的三视图,则组成这个几何体的玩具个数最少为 个;
(3)由于旗舰店在双十一期间推出买一送一的活动,现要将两个同一型号的乐高积木包装在同一个大长方体的外包装盒内(如图1),已知单个乐高积木的长方体纸盒长和高相等,且宽小于长.如图3所示,现有甲,乙两种摆放方式,请分别计算甲,乙两种摆放方式所需外包装盒的纸板面积(包装盒上盖朝上),并比较哪一种方式所需纸板面积更少,说明理由.
参考答案与试题解析
一.选择题
1.【解答】解:A、从正面看到的是矩形,从左面看到的是正方形,故本选项符合题意;
B、从正面看到的是三角形,从左面看到的是三角形,故本选项不合题意;
C、从正面看到的是圆,从左面看到的是圆,故本选项不合题意;
D、从正面看到的是矩形,从左面看到的是矩形,故本选项不合题意;
故选:A.
2.【解答】解:从上面看:共分3列,从左往右分别有2,2,1个小正方形.
故选:A.
3.【解答】解:该几何体的主视图与左视图相同,底层是一个矩形,上层的中间是一个矩形;俯视图是两个同心圆.
故选:A.
4.【解答】解:从正面看易得第一层有3个正方形,第二层最左边有一个正方形,右边是一个三角形.
故选:C.
5.【解答】解:从正面看,底层是三个小正方形,上层的右边是一个小正方形.
故选:A.
6.【解答】解:从左边看,是一个矩形,矩形的中间有一条横向的虚线.
故选:D.
7.【解答】解:∵正多边形的内角和公式为:(n﹣2)×180°,
∴正五边形的内角和是:(5﹣2)×180°=540°,
则每个内角是:540°÷5=108°.
故选:B.
8.【解答】解:将正方体①移走前的主视图正方形的个数为1,2,1;正方体①移走后的主视图正方形的个数为1,2;主视图发生改变.
将正方体①移走前的左视图正方形的个数为2,1,1;正方体①移走后的左视图正方形的个数为2,1,1;左视图没有发生改变.
将正方体①移走前的俯视图正方形的个数为1,3,1;正方体①移走后的俯视图正方形的个数,1,3;俯视图发生改变.
故选:D.
9.【解答】解:从左边看的图形为:
故选:D.
10.【解答】解:从上面看可得到一个正方形,正方形里面有一条撇向的实线.
故选:C.
二.填空题(共5小题)
11.【解答】解:由俯视图易得最底层有4个小正方体,第二层最多有2个小正方体,那么搭成这个几何体的小正方体最多为4+2=6个.
故答案为:6
12.【解答】解:最下面一层有4块,
上面一层最少有2块,最多有4块,
故搭这个立体图形需要6或7或8块小立方体.
故答案为:6或7或8.
13.【解答】解:综合三视图,我们可以得出,这个几何模型的底层有2+1=3个小正方体,第二层应该有1个小正方体,
因此搭成这个几何体模型所用的小正方体的个数是3+1=4个.
所以表面积为3×6=18cm2.
故答案为:18cm2.
14.【解答】解:观察三视图可知,这个立体图形想底面为半圆的半个圆柱(如图所示).
V=π12×2=π,
故答案为π.
15.【解答】解:由勾股定理可得:底面圆的半径==3,则底面周长=6π,
由图得,母线长=5,
侧面面积=×6π×5=15π.
故选:15π.
三.解答题(共4小题)
16.【解答】解:(1)由主视图可得,俯视图中最右边一正方形处有3个小立方体,中间一列两个正方形处各有1个小立方体,
则a=3,b=1,c=1;
(2)若d,e,f处,有一处为2个小立方体,其余两处各有1个小立方体,则该几何体最少有9个小立方体搭成;
若d,e,f处,各有2个小立方体,则该几何体最多有11个小立方体搭成;
(3)当d=1,e=2,f=1时,几何体的左视图为:
.
17.【解答】解:(1)几何体的名称是三棱柱;
(2)表面展开图为:
(3)3×4×3=36cm2,
∴这个几何体的侧面积为36 cm2.
18.【解答】解:(1)几何体的体积:1×1×1×5=5(立方单位).
故该几何体的体积是5立方单位;
(2)如图所示:
故答案为:5.
19.【解答】解:(1)制作长方体纸箱需要(2ac+2bc+3ab)平方厘米纸板;
故答案为:(2ac+2bc+3ab);
(2)根据三视图知,则组成这个几何体的玩具个数最少的分布情况如下图所示:
所以组成这个几何体的玩具个数最少为9个,
故答案为:9;
(3)如图3,由题意得:a=c,a>b,
甲:2(ac+2bc+2ab)+2ab,
乙:2(2ab+2ac+bc)+2ab,
∵a>b,
∴ac>bc,
∴ac﹣bc>0,
∵甲所需纸板面积﹣乙所需纸板面积=2(ac+2bc﹣2ac﹣bc)=2(bc﹣ac)<0,
∴甲种摆放方式所需外包装盒的纸板面积更少.
