人教版数学九年级下册第二十七章《相似》全章基础拔高质量检测卷(Word版 含解析)
文档属性
| 名称 | 人教版数学九年级下册第二十七章《相似》全章基础拔高质量检测卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 15:05:40 | ||
图片预览


文档简介
九年级下册人教版数学第二十七章《相似》全章基础拔高质量检测卷
一、单选题
1.若=,则的值为( )
A. B. C. D.
2.如图,直线,,,则的长为( )
A. B. C. D.
3.下列命题中,说法正确的是( )
A.四条边对应成比例的两个四边形相似
B.四个内角对应相等的两个四边形相似
C.两边对应成比例且有一个角相等的两个三角形相似
D.斜边与一条直角边对应成比例的两个直角三角形相似
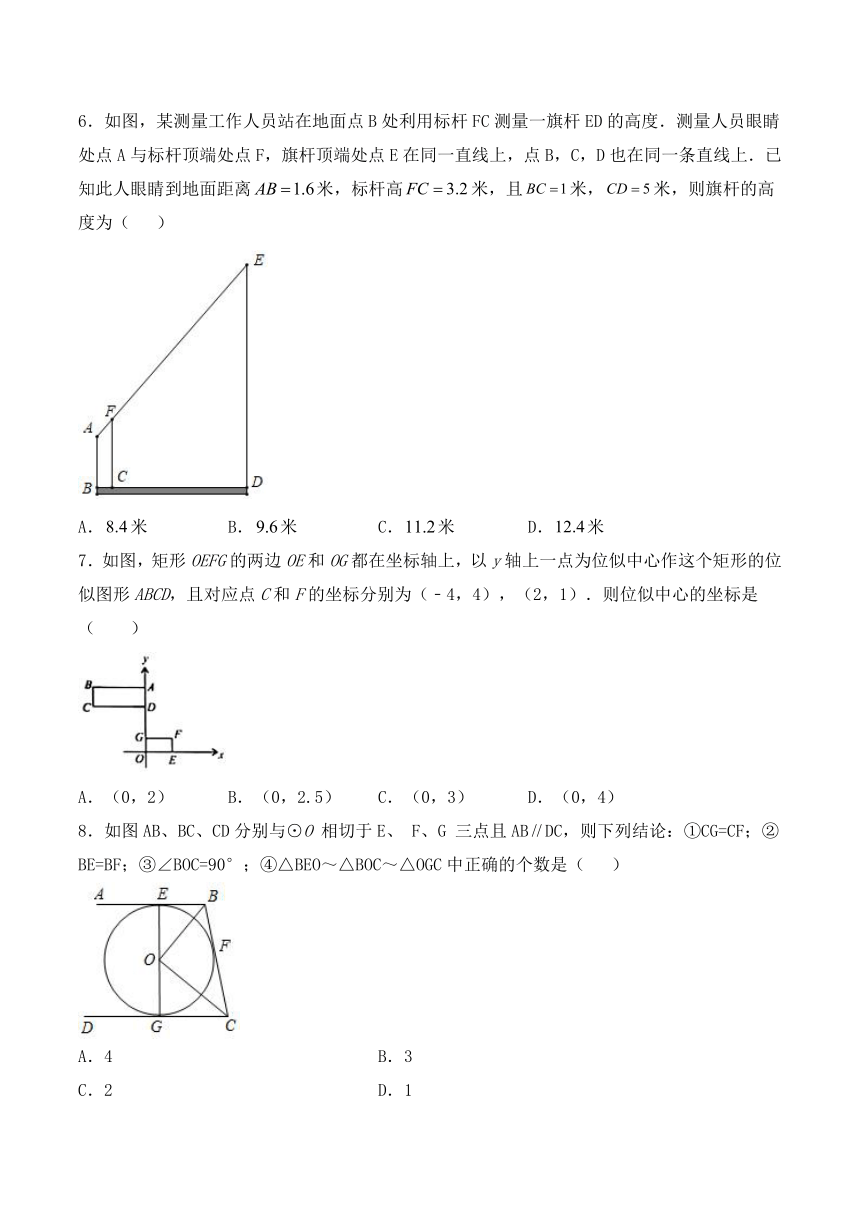
4.如图,中,、两点分别在、上,且平分,若,与相交于点.则图中相似三角形的对数是( )
A.1 B.2 C.3 D.4
5.如图,在△ABC中,DE∥BC,且S△ADE:S△CDE=1:3,则S△ADE:S△DBC等于( )
A.1:5 B.1:12 C.1:8 D.1:9
6.如图,某测量工作人员站在地面点B处利用标杆FC测量一旗杆ED的高度.测量人员眼睛处点A与标杆顶端处点F,旗杆顶端处点E在同一直线上,点B,C,D也在同一条直线上.已知此人眼睛到地面距离米,标杆高米,且米,米,则旗杆的高度为( )
A.米 B.米 C.米 D.米
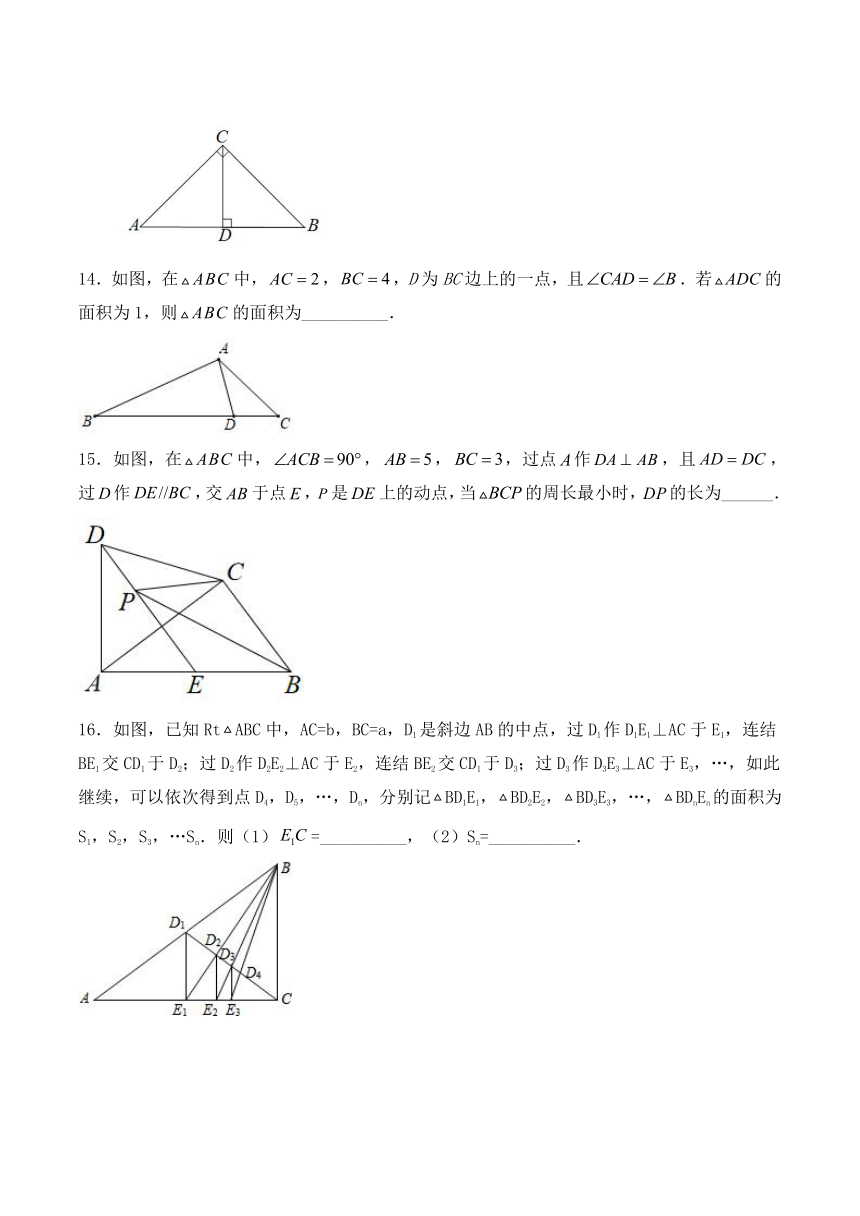
7.如图,矩形OEFG的两边OE和OG都在坐标轴上,以y轴上一点为位似中心作这个矩形的位似图形ABCD,且对应点C和F的坐标分别为(﹣4,4),(2,1).则位似中心的坐标是( )
A.(0,2) B.(0,2.5) C.(0,3) D.(0,4)
8.如图AB、BC、CD分别与⊙O 相切于E、 F、G 三点且ABDC,则下列结论:①CG=CF;②BE=BF;③∠BOC=90°;④△BEO~△BOC~△OGC中正确的个数是( )
A.4 B.3
C.2 D.1
9.如图,平行四边形中,点为边中点,连接、交于点,若的面积为关于的一元二次方程的解,则的面积为( ).
A.4 B.5 C.6 D.7
10.如图,在中,,,,点P为平面内一点,且,过C作交PB的延长线于点Q,则CQ的最大值为( )
A. B. C. D.
二、填空题
11.如图,若点B是线段AC的黄金分割点,,则________.
12.如图,在△ABC中,,且AD:AF:AB=1:2:4,则S△ADE:S四边形DFGE:S四边形FBCG等于______
13.如图,在中,,于点D,如果,,那么__________.
14.如图,在中,,,D为BC边上的一点,且.若的面积为1,则的面积为__________.
15.如图,在中,,,,过点作,且,过作,交于点,是上的动点,当的周长最小时,的长为______.
16.如图,已知RtABC中,AC=b,BC=a,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连结BE1交CD1于D2;过D2作D2E2⊥AC于E2,连结BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点D4,D5,…,Dn,分别记BD1E1,BD2E2,BD3E3,…,BDnEn的面积为S1,S2,S3,…Sn.则(1)=__________,(2)Sn=__________.
三、解答题
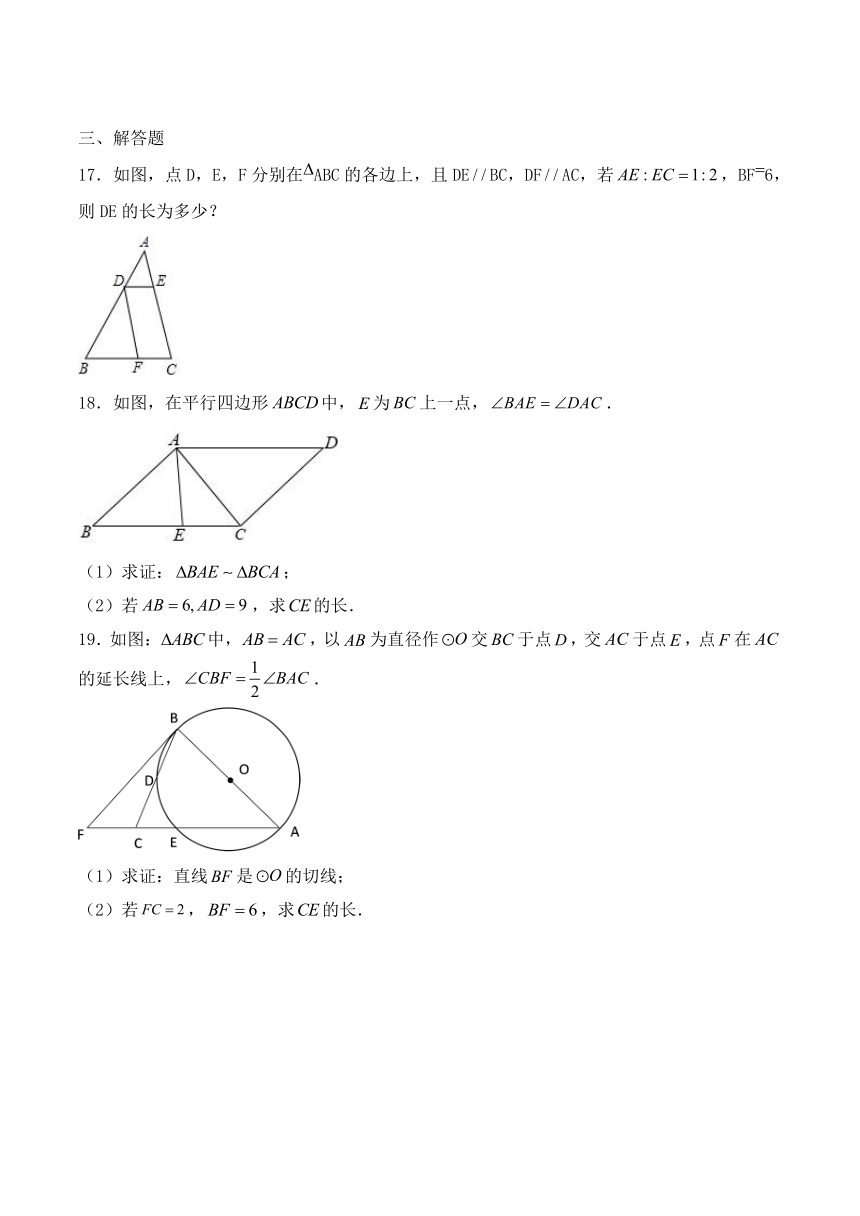
17.如图,点D,E,F分别在ABC的各边上,且DEBC,DFAC,若,BF6,则DE的长为多少?
18.如图,在平行四边形中,为上一点,.
(1)求证:;
(2)若,求的长.
19.如图:中,,以为直径作交于点,交于点,点在的延长线上,.
(1)求证:直线是的切线;
(2)若,,求的长.
20.如图,在平行四边形中,,点、是对角线上的两点,且,的延长线交于点,的延长线交于点.
(1)求的长;
(2)设的面积为,求四边形的面积.(用含的代数式表示)
21.在平面直角坐标系中,直线与函数,的图象交于点.
(1)求,的值;
(2)点是函数,的图象上任意一点(不与点重合),点,在直线上,点横坐标为.若,求点横坐标的取值范围.
22.如图,在?ABC中,AB=BC=10,AC=12,动点D从点B开始在线段BA上以每秒1个单位长度的速度向点A移动,同时动点E从点A开始在线段AE上以每秒2个单位长度的速度向点C移动,当其中一个点到达终点时,另一个点也随之停止,设点D、E移动的时间为t.
(1)用含t的代数式表示:AD= ,AE= ;
(2)当DE//BC时,求t的值;
(3)当t为何值时,?ADE为直角三角形.
参考答案与解析
1.A
=,
,
;
2.B
由题意可知,
又∵BC=BE-CE=16-CE,
∴,
∴.
3.D
A、四个角对应相等,四条边对应成比例的两个四边形相似,原命题是假命题;
B、四个内角对应相等,四条边对应成比例的两个四边形相似,原命题是假命题;
C、两边对应成比例且其夹角相等的两个三角形相似,原命题是假命题;
D、斜边与一条直角边对应成比例的两个直角三角形相似,是真命题;
4.C
解:如图,设∠BAD=∠1,∠CAD=∠2,则
①在△ABE与△ACB中,∠ABE=∠C,∠BAE=∠CAB,
∴△ABE~△ACB;
②∵AD平分∠BAC,∴∠1=∠2.
∵∠1=∠2,∠ABF=∠C,
∴△ABF∽△ACD;
③∵ABE~△ACB,
∴∠BEA=∠ABD,
又∵∠1=∠2,
∴△AEF∽△ABD,
综合①②③知,共有3对相似三角形,
5.B
解:∵△ADE的边AE上的高和△CDE的边CE上的高相等,
∵S△ADE:S△CDE=1:3,
∴,
∵DE∥BC,
∴,
∴ ,
∵DE∥BC,
∴△ADE∽△ABC,
∴,
设S△ADE=k,则S△CDE=3k,S△ABC=16k,
∴S△BCD=S△ABC-S△ADE-S△CDE=12k,
∴S△ADE:S△DBC=1:12.
6.C
解:作交FC于点G,如图所示:
,,交FC于点G,
,
,,,,
∴四边形ABDH、ABCG是矩形,
,,
,,,,
,,
,
,
解得:,
答:旗杆的高ED是米,
7.A
解:如图,连接CF交y轴于P,
∵四边形ABCD和四边形EFGO是矩形,点C,F的坐标分别为(-4,4),(2,1),
∴点D的坐标为(0,4),点G的坐标为(0,1),
∴DG=3,
∵CD∥GF,
∴,
∴GP=1,PD=2,
∴点P的坐标为(0,2),
8.A
连结OF,
∵AB、BC、CD分别与⊙O 相切于E、 F、G,
又因为CG与CF为切线长,BE与BF也为切线长,
∴CG=CF,BE=BF,
∴①CG=CF,②BE=BF正确;
∵AB、BC、CD分别与⊙O 相切于E、 F、G,
∴OE⊥AB,OF⊥BC,OG⊥CD,
∴∠OEB=∠OFB=∠OFC=∠OGC=90?,
∴OB平分∠EBF,OC平分∠FCG,
∴∠EBO=∠FBO,∠FCO=∠GCO,
∴△BEO≌△BFO(AAS),△FCO≌△GCO(AAS),
∴∠EOB=∠FOB,∠FOC=∠GOC,
∵∠EOB+∠FOB+∠FOC+∠GOC=180?,
∴2∠FOB+2∠FOC=180?,
∴∠FOB+∠FOC=90?,
∴∠BOC=∠FOB+∠FOC=90?,
∴③∠BOC=90°正确;;
由△OBC、△BEO、△CGO都是直角三角形,
∵∠EOB+∠EBO=90?,∠EOB+∠EBO=90?,
∴∠GOC=∠EBO=∠OBC,
△BEO∽△BOC∽△OGC,
∴④△BEO~△BOC~△OGC正确,
①CG=CF;②BE=BF;③∠BOC=90°;④△BEO~△BOC~△OGC中正确的个数有4个,
故选择:A.
9.A
解:,
(x+2)(x?1)=0,
解得x1=?2(舍去),x2=1.
则△AEF的面积为1.
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∴△AFE∽△CFB.
∵点E为AD边中点,
∴AE=AD=BC,则.
∴,即.
解得S△FBC=4.
10.B
解:∵在中,,,,
∴A、B、C、P四点共圆,AB为圆的直径,AB=
∵
∴
∴△ABC∽△PQC
∴, ,即
∴当PC取得最大值时,CQ即为最大值
∴当PC=AB=5时,CQ取得最大值为
11.
解:因为点B是线段AC的黄金分割点(AB>BC),
∴AB2=BC?AC,∴,
∴AB=AC,
∴=,
故答案为:.
12.1:3:12
解:∵DE∥FG∥BC,
∴△ADE∽△AFG∽△ABC,
∵AD:AF:AB=1:2:4,
∴S△ADE:S△AFG:S△ABC=1:4:16,
设△ADE的面积是a,则△AFG和△ABC的面积分别是4a,16a,
则S四边形DFGE和S四边形FBCG分别是3a,12a,
∴S△ADE:S四边形DFGE:S四边形FBCG=1:3:12.
故答案为:1:3:12.
13.9
解:∵CD⊥AB,
∴∠CDA=∠CDB=90°,
∴∠ACD+∠A=90°,
又∵∠ACB=90°,
∴∠ACD+∠DCB=90°,
∴∠DCB=∠A
在△ACD和△CBD中,
∴△ACD∽△CBD
∴
∵AC=6,AD=3,
∴由勾股定理得,CD==3,
∴
∴BD=9
14.4
∵∠CAD=∠B,∠ACD=∠BCA,
∴△ACD∽△BCA,
∴,
∵AC=2,BC=4,△ACD的面积为1,
∴,
∴S△ABC=4.
15.
解:如图,连接.
∵,,
∴.
又∵,
∴DE是线段AC的垂直平分线,
∴点在线段的垂直平分线上.
∴,,
∴要使的周长最小,只要最小即可.
∵,
∴当与重合时,最小.
∵,,
∴,.
∵,
∴,
∴.
∴,
即.
故答案为:.
16.b
解:∵D1E1⊥AC,BC⊥AC,
∴D1E1∥BC,
∴,
∵D1是斜边AB的中点,
∴AD1=BD1,
∴,
∵AC=b,
∴AE1=E1C=b,
∵D1E1∥BC,
∴BD1E1与CD1E1同底同高,面积相等,以此类推;
根据直角三角形的性质以及相似三角形的性质可知:D1E1=BC,CE1=AC,S1=S△ABC;
∴在ACB中,D2为其重心,
∴D2E1=BE1,
∴D2E2=BC,CE2=AC,S2=S△ABC,
∵D2E2:D1E1=2:3,D1E1:BC=1:2,
∴BC:D2E2=2D1E1:D1E1=3,
∴CD3:CD2=D3E3:D2E2=CE3:CE2=3:4,
∴D3E3=D2E2=×BC=BC,CE3=CE2=×AC=AC,S3=S△ABC…;
∴Sn=S△ABC=×ab=.
故答案为:b,.
17.3
解:∵DE//BC,DF//AC,
∴四边形DECF为平行四边形,
∴DE=CF,
∵DE//BC,
∴,
∵AE:EC=1:2,
∴AE:AC=1:3,
∴,
∴DE=3.
18.
解:(1)证明:∵四边形是平行四边形,
∴,
∴,
∵,
∴
又∵,
∴;
(2)∵四边形是平行四边形
∴,
由(1)知:,
∴,
∴,
∴,
∴
19.
(1)证明:连接,
∵是的直径,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,即,
∵是的半径,
∴是的切线.
(2)设,则,
在中,
∵,
∴,解得,
∴,,
连接,
∵是的直径,
∴,
∴,
又∵,
∴,
∴,
∴
∴.
20.
解:(1)∵四边形是平行四边形,
∴AD//BC,AD=BC=8,
∴△ADE∽△GBE,
∴.
∵,
∴BG=AD=4.
∵AD//BC,
∴△HDF∽△GBF,
∴.
∵,
∴HD=BG=2;
(2)∵△ADE∽△GBE, ,
∴S△ADE=4S△BGE=4a.
∵△HDF∽△GBF,
∴S△DHF=S△BGF.
∵,
∴S△BGF=2S△BGE,
∴S△DHF=S△BGE=a,
∴.
21.
解:(1) 点在直线上,
,
函数,的图象经过点,
.
(2) 设点到直线的距离为.
,,
,
.
,点横坐标为,
如图,当点在射线上时,;过A作AD⊥x轴,交过P、Q分别与x轴平行的直线与C、D,由QC∥PD,
∴△AQC∽△APD,
即,
,
如图,当点在线段延长线上时,过P作PF∥x轴,与过A、Q作y轴的平行线交于E,F,
∵AE∥QF,
∴△PAE∽△PQF,
∴即,
∴即
.
综上所述:点横坐标的取值范围或.
22.
解:(1)由题意得:AD=AB-BD,
∴AD= 10-t,AE=2t;
(2)当DE//BC时,,
∴,解得
∴当DE//BC时,s.
(3)如图,过点B作BH⊥AC于点H,
∵AB=BC,
∴,
∵∠A=∠A,
∴当时,?ADE∽?ABH,?ADE为直角三角形,
∴,解得,
当时,?ADE∽?AHB,?ADE为直角三角形,
∴,解得.
综上所述,当s或s时,?ADE为直角三角形.
一、单选题
1.若=,则的值为( )
A. B. C. D.
2.如图,直线,,,则的长为( )
A. B. C. D.
3.下列命题中,说法正确的是( )
A.四条边对应成比例的两个四边形相似
B.四个内角对应相等的两个四边形相似
C.两边对应成比例且有一个角相等的两个三角形相似
D.斜边与一条直角边对应成比例的两个直角三角形相似
4.如图,中,、两点分别在、上,且平分,若,与相交于点.则图中相似三角形的对数是( )
A.1 B.2 C.3 D.4
5.如图,在△ABC中,DE∥BC,且S△ADE:S△CDE=1:3,则S△ADE:S△DBC等于( )
A.1:5 B.1:12 C.1:8 D.1:9
6.如图,某测量工作人员站在地面点B处利用标杆FC测量一旗杆ED的高度.测量人员眼睛处点A与标杆顶端处点F,旗杆顶端处点E在同一直线上,点B,C,D也在同一条直线上.已知此人眼睛到地面距离米,标杆高米,且米,米,则旗杆的高度为( )
A.米 B.米 C.米 D.米
7.如图,矩形OEFG的两边OE和OG都在坐标轴上,以y轴上一点为位似中心作这个矩形的位似图形ABCD,且对应点C和F的坐标分别为(﹣4,4),(2,1).则位似中心的坐标是( )
A.(0,2) B.(0,2.5) C.(0,3) D.(0,4)
8.如图AB、BC、CD分别与⊙O 相切于E、 F、G 三点且ABDC,则下列结论:①CG=CF;②BE=BF;③∠BOC=90°;④△BEO~△BOC~△OGC中正确的个数是( )
A.4 B.3
C.2 D.1
9.如图,平行四边形中,点为边中点,连接、交于点,若的面积为关于的一元二次方程的解,则的面积为( ).
A.4 B.5 C.6 D.7
10.如图,在中,,,,点P为平面内一点,且,过C作交PB的延长线于点Q,则CQ的最大值为( )
A. B. C. D.
二、填空题
11.如图,若点B是线段AC的黄金分割点,,则________.
12.如图,在△ABC中,,且AD:AF:AB=1:2:4,则S△ADE:S四边形DFGE:S四边形FBCG等于______
13.如图,在中,,于点D,如果,,那么__________.
14.如图,在中,,,D为BC边上的一点,且.若的面积为1,则的面积为__________.
15.如图,在中,,,,过点作,且,过作,交于点,是上的动点,当的周长最小时,的长为______.
16.如图,已知RtABC中,AC=b,BC=a,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连结BE1交CD1于D2;过D2作D2E2⊥AC于E2,连结BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点D4,D5,…,Dn,分别记BD1E1,BD2E2,BD3E3,…,BDnEn的面积为S1,S2,S3,…Sn.则(1)=__________,(2)Sn=__________.
三、解答题
17.如图,点D,E,F分别在ABC的各边上,且DEBC,DFAC,若,BF6,则DE的长为多少?
18.如图,在平行四边形中,为上一点,.
(1)求证:;
(2)若,求的长.
19.如图:中,,以为直径作交于点,交于点,点在的延长线上,.
(1)求证:直线是的切线;
(2)若,,求的长.
20.如图,在平行四边形中,,点、是对角线上的两点,且,的延长线交于点,的延长线交于点.
(1)求的长;
(2)设的面积为,求四边形的面积.(用含的代数式表示)
21.在平面直角坐标系中,直线与函数,的图象交于点.
(1)求,的值;
(2)点是函数,的图象上任意一点(不与点重合),点,在直线上,点横坐标为.若,求点横坐标的取值范围.
22.如图,在?ABC中,AB=BC=10,AC=12,动点D从点B开始在线段BA上以每秒1个单位长度的速度向点A移动,同时动点E从点A开始在线段AE上以每秒2个单位长度的速度向点C移动,当其中一个点到达终点时,另一个点也随之停止,设点D、E移动的时间为t.
(1)用含t的代数式表示:AD= ,AE= ;
(2)当DE//BC时,求t的值;
(3)当t为何值时,?ADE为直角三角形.
参考答案与解析
1.A
=,
,
;
2.B
由题意可知,
又∵BC=BE-CE=16-CE,
∴,
∴.
3.D
A、四个角对应相等,四条边对应成比例的两个四边形相似,原命题是假命题;
B、四个内角对应相等,四条边对应成比例的两个四边形相似,原命题是假命题;
C、两边对应成比例且其夹角相等的两个三角形相似,原命题是假命题;
D、斜边与一条直角边对应成比例的两个直角三角形相似,是真命题;
4.C
解:如图,设∠BAD=∠1,∠CAD=∠2,则
①在△ABE与△ACB中,∠ABE=∠C,∠BAE=∠CAB,
∴△ABE~△ACB;
②∵AD平分∠BAC,∴∠1=∠2.
∵∠1=∠2,∠ABF=∠C,
∴△ABF∽△ACD;
③∵ABE~△ACB,
∴∠BEA=∠ABD,
又∵∠1=∠2,
∴△AEF∽△ABD,
综合①②③知,共有3对相似三角形,
5.B
解:∵△ADE的边AE上的高和△CDE的边CE上的高相等,
∵S△ADE:S△CDE=1:3,
∴,
∵DE∥BC,
∴,
∴ ,
∵DE∥BC,
∴△ADE∽△ABC,
∴,
设S△ADE=k,则S△CDE=3k,S△ABC=16k,
∴S△BCD=S△ABC-S△ADE-S△CDE=12k,
∴S△ADE:S△DBC=1:12.
6.C
解:作交FC于点G,如图所示:
,,交FC于点G,
,
,,,,
∴四边形ABDH、ABCG是矩形,
,,
,,,,
,,
,
,
解得:,
答:旗杆的高ED是米,
7.A
解:如图,连接CF交y轴于P,
∵四边形ABCD和四边形EFGO是矩形,点C,F的坐标分别为(-4,4),(2,1),
∴点D的坐标为(0,4),点G的坐标为(0,1),
∴DG=3,
∵CD∥GF,
∴,
∴GP=1,PD=2,
∴点P的坐标为(0,2),
8.A
连结OF,
∵AB、BC、CD分别与⊙O 相切于E、 F、G,
又因为CG与CF为切线长,BE与BF也为切线长,
∴CG=CF,BE=BF,
∴①CG=CF,②BE=BF正确;
∵AB、BC、CD分别与⊙O 相切于E、 F、G,
∴OE⊥AB,OF⊥BC,OG⊥CD,
∴∠OEB=∠OFB=∠OFC=∠OGC=90?,
∴OB平分∠EBF,OC平分∠FCG,
∴∠EBO=∠FBO,∠FCO=∠GCO,
∴△BEO≌△BFO(AAS),△FCO≌△GCO(AAS),
∴∠EOB=∠FOB,∠FOC=∠GOC,
∵∠EOB+∠FOB+∠FOC+∠GOC=180?,
∴2∠FOB+2∠FOC=180?,
∴∠FOB+∠FOC=90?,
∴∠BOC=∠FOB+∠FOC=90?,
∴③∠BOC=90°正确;;
由△OBC、△BEO、△CGO都是直角三角形,
∵∠EOB+∠EBO=90?,∠EOB+∠EBO=90?,
∴∠GOC=∠EBO=∠OBC,
△BEO∽△BOC∽△OGC,
∴④△BEO~△BOC~△OGC正确,
①CG=CF;②BE=BF;③∠BOC=90°;④△BEO~△BOC~△OGC中正确的个数有4个,
故选择:A.
9.A
解:,
(x+2)(x?1)=0,
解得x1=?2(舍去),x2=1.
则△AEF的面积为1.
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∴△AFE∽△CFB.
∵点E为AD边中点,
∴AE=AD=BC,则.
∴,即.
解得S△FBC=4.
10.B
解:∵在中,,,,
∴A、B、C、P四点共圆,AB为圆的直径,AB=
∵
∴
∴△ABC∽△PQC
∴, ,即
∴当PC取得最大值时,CQ即为最大值
∴当PC=AB=5时,CQ取得最大值为
11.
解:因为点B是线段AC的黄金分割点(AB>BC),
∴AB2=BC?AC,∴,
∴AB=AC,
∴=,
故答案为:.
12.1:3:12
解:∵DE∥FG∥BC,
∴△ADE∽△AFG∽△ABC,
∵AD:AF:AB=1:2:4,
∴S△ADE:S△AFG:S△ABC=1:4:16,
设△ADE的面积是a,则△AFG和△ABC的面积分别是4a,16a,
则S四边形DFGE和S四边形FBCG分别是3a,12a,
∴S△ADE:S四边形DFGE:S四边形FBCG=1:3:12.
故答案为:1:3:12.
13.9
解:∵CD⊥AB,
∴∠CDA=∠CDB=90°,
∴∠ACD+∠A=90°,
又∵∠ACB=90°,
∴∠ACD+∠DCB=90°,
∴∠DCB=∠A
在△ACD和△CBD中,
∴△ACD∽△CBD
∴
∵AC=6,AD=3,
∴由勾股定理得,CD==3,
∴
∴BD=9
14.4
∵∠CAD=∠B,∠ACD=∠BCA,
∴△ACD∽△BCA,
∴,
∵AC=2,BC=4,△ACD的面积为1,
∴,
∴S△ABC=4.
15.
解:如图,连接.
∵,,
∴.
又∵,
∴DE是线段AC的垂直平分线,
∴点在线段的垂直平分线上.
∴,,
∴要使的周长最小,只要最小即可.
∵,
∴当与重合时,最小.
∵,,
∴,.
∵,
∴,
∴.
∴,
即.
故答案为:.
16.b
解:∵D1E1⊥AC,BC⊥AC,
∴D1E1∥BC,
∴,
∵D1是斜边AB的中点,
∴AD1=BD1,
∴,
∵AC=b,
∴AE1=E1C=b,
∵D1E1∥BC,
∴BD1E1与CD1E1同底同高,面积相等,以此类推;
根据直角三角形的性质以及相似三角形的性质可知:D1E1=BC,CE1=AC,S1=S△ABC;
∴在ACB中,D2为其重心,
∴D2E1=BE1,
∴D2E2=BC,CE2=AC,S2=S△ABC,
∵D2E2:D1E1=2:3,D1E1:BC=1:2,
∴BC:D2E2=2D1E1:D1E1=3,
∴CD3:CD2=D3E3:D2E2=CE3:CE2=3:4,
∴D3E3=D2E2=×BC=BC,CE3=CE2=×AC=AC,S3=S△ABC…;
∴Sn=S△ABC=×ab=.
故答案为:b,.
17.3
解:∵DE//BC,DF//AC,
∴四边形DECF为平行四边形,
∴DE=CF,
∵DE//BC,
∴,
∵AE:EC=1:2,
∴AE:AC=1:3,
∴,
∴DE=3.
18.
解:(1)证明:∵四边形是平行四边形,
∴,
∴,
∵,
∴
又∵,
∴;
(2)∵四边形是平行四边形
∴,
由(1)知:,
∴,
∴,
∴,
∴
19.
(1)证明:连接,
∵是的直径,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,即,
∵是的半径,
∴是的切线.
(2)设,则,
在中,
∵,
∴,解得,
∴,,
连接,
∵是的直径,
∴,
∴,
又∵,
∴,
∴,
∴
∴.
20.
解:(1)∵四边形是平行四边形,
∴AD//BC,AD=BC=8,
∴△ADE∽△GBE,
∴.
∵,
∴BG=AD=4.
∵AD//BC,
∴△HDF∽△GBF,
∴.
∵,
∴HD=BG=2;
(2)∵△ADE∽△GBE, ,
∴S△ADE=4S△BGE=4a.
∵△HDF∽△GBF,
∴S△DHF=S△BGF.
∵,
∴S△BGF=2S△BGE,
∴S△DHF=S△BGE=a,
∴.
21.
解:(1) 点在直线上,
,
函数,的图象经过点,
.
(2) 设点到直线的距离为.
,,
,
.
,点横坐标为,
如图,当点在射线上时,;过A作AD⊥x轴,交过P、Q分别与x轴平行的直线与C、D,由QC∥PD,
∴△AQC∽△APD,
即,
,
如图,当点在线段延长线上时,过P作PF∥x轴,与过A、Q作y轴的平行线交于E,F,
∵AE∥QF,
∴△PAE∽△PQF,
∴即,
∴即
.
综上所述:点横坐标的取值范围或.
22.
解:(1)由题意得:AD=AB-BD,
∴AD= 10-t,AE=2t;
(2)当DE//BC时,,
∴,解得
∴当DE//BC时,s.
(3)如图,过点B作BH⊥AC于点H,
∵AB=BC,
∴,
∵∠A=∠A,
∴当时,?ADE∽?ABH,?ADE为直角三角形,
∴,解得,
当时,?ADE∽?AHB,?ADE为直角三角形,
∴,解得.
综上所述,当s或s时,?ADE为直角三角形.
