北师大版九年级数学下册 第3章 圆 单元测试题(Word版 含答案)
文档属性
| 名称 | 北师大版九年级数学下册 第3章 圆 单元测试题(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 251.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 15:16:30 | ||
图片预览

文档简介
1148080012026900123190000第3章 圆 单元测试题
(满分100分;时间:90分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 下列命题中,正确的个数是( )
(1)直径是弦,但弦不一定是直径;(2)半圆是弧,但弧不一定是半圆;
(3)半径相等的两个圆是等圆;(4)一条弦把圆分成的两段弧中,至少有一段是优弧.
A.1个 B.2个 C.3个 D.4个
?
2. 已知⊙O的半径为5,直线EF经过⊙O上一点P(点E,F在点P的两旁),下列条件能判定直线EF与⊙O相切的是( )
A.OP=5 B.OE=OF
C.O到直线EF的距离是4 D.OP⊥EF
?3. 如图,PA,PB为⊙O的切线,A,B分别为切点,∠APB=60?,点P到圆心O的距离OP=2,则⊙O的半径为(? ? ? ? )
A.12 B.1 C.32 D.2
?
4. 《九章算术》中“今有勾七步,股有二十四步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为7步,股(长直角边)长为24步,问该直角三角形的容圆(内切圆)直径是多少?”( )
A.4步 B.5步 C.6步 D.8步
?5. ⊙O的半径为2,△ABC是⊙O的内接三角形,连接OB,OC.若∠BAC与∠BOC互补,则弦BC的长为(? ? ? ? )
A.43 B.33 C.23 D.3
?
6. 如图,PA,PB分别切⊙O于点A和点B,C是AB上任一点,过C的切线分别交PA,PB于D,E.若⊙O的半径为6,PO=10,则△PDE的周长是( )
A.16 B.14 C.12 D.10
?
7. 如图,PT切⊙O于点T,经过圆心O的割线PAB交⊙O于点A、B,已知PT=4,PA=2,则⊙O的直径AB等于( )
A.3 B.4 C.6 D.8
?
8. 如图,已知点E是圆O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46?,则∠AED的度数为( )
A.138? B.46? C.69? D.92?
?9. 如图,已知AB是⊙O的直径,AD切⊙O于点A,EC=CB.则下列结论中不一定正确的是(? ? ? ? )
A.BA⊥DA B.OC?//?AE
C.∠COE=2∠CAE D.OD⊥AC
?10. 如图,一条公路的转弯处是一段圆弧(AB),点O是这段弧所在圆的圆心,∠AOB=60?,点C是AB的中点,且CD=5m,则这段弯路所在圆的半径为( )
A.(20-103)m B.20m C.30m D.(20+103)m
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
11. 如图,AB是⊙O的直径,点C、D是圆上位于AB两侧的点,若∠BAC=58?,则∠D=________??.
?
12. 已知扇形的圆心角为120?,弧长等于一个半径为5cm的圆的周长,则扇形的面积为________.
?
13. 如图,四边形ABCD内接于⊙O,∠C=110?,连接OB、OD,则∠BOD=________.
?
14. 如图,在Rt△ABC中,∠B=90?,AB=6,BC=8,⊙O为△ABC的内切圆,M、N分别在边AC、BC上,且MN?//?AB,MN切⊙O于D点,则MO=________.
?
15. 已知:如图,在⊙O中,弦AB、CD相交于点P,PA=2,PB=6,PC=3,则CD=________.
?
16. 如图,直角△ABC的直角顶点C,另一顶点A及斜边AB的中点D都在⊙O上,已知:AC=6,BC=8,则⊙O的半径为________.
?
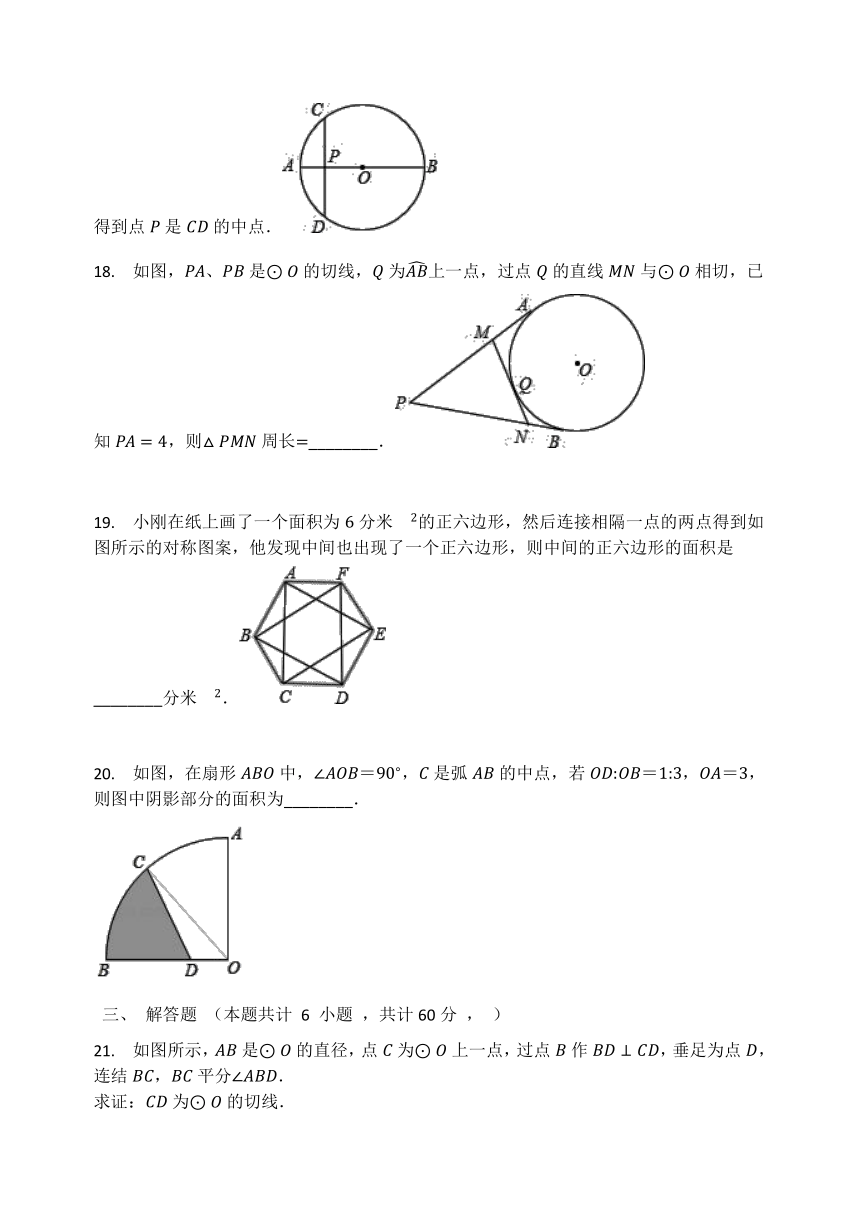
17. 如图,⊙O的直径AB与弦CD交于点P,添加条件________(写出一个即可),就可得到点P是CD的中点. ?
18. 如图,PA、PB是⊙O的切线,Q为AB上一点,过点Q的直线MN与⊙O相切,已知PA=4,则△PMN周长=________.
?
19. 小刚在纸上画了一个面积为6分米?2的正六边形,然后连接相隔一点的两点得到如图所示的对称图案,他发现中间也出现了一个正六边形,则中间的正六边形的面积是________分米?2.
?
20. 如图,在扇形ABO中,∠AOB=90?,C是弧AB的中点,若OD:OB=1:3,OA=3,则图中阴影部分的面积为________.
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
21. 如图所示,AB是⊙O的直径,点C为⊙O上一点,过点B作BD⊥CD,垂足为点D,连结BC,BC平分∠ABD.
求证:CD为⊙O的切线.
?
22. 已知:如图,△ABC内接于⊙O,过A点作直线DE,当∠BAE=∠C时,试确定直线DE与⊙O的位置关系,并证明你的结论.
?
23. 如图,已知AB是⊙O的直径,P为AB延长线上的一点,PC是⊙O的切线,C为切点,∠A=35?,求∠P的度数.
?
24. 如图,在△ABC中,∠A=72?,点I是△ABC内的一点.
(1)若点I是△ABC的内心,求∠BIC的度数;
(2)若点I是△ABC的外心,求∠BIC的度数.
?
25. 如图,在⊙O中,点C为AB的中点,∠ACB=120?,OC的延长线与AD交于点D,且∠D=∠B.
(1)求证:AD与⊙O相切;
(2)若CE=4,求弦AB的长.
?
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
【解答】
解:当弦为直径时,不会把圆分成一段优弧一段劣弧,
∴ (4)为假命题
而(1)、(2)、(3)均正确
故选C.
2.
【答案】
D
【解答】
∵ 点P在⊙O上,
∴ 只需要OP⊥EF即可,
3.
【答案】
B
【解答】
解:如图,连接OA,OB,
∵ PA,PB为⊙O的切线交于点P,
∴ PA⊥OA,PB⊥OB,OA=OB.
由角平分线定义可知:∠APO=12∠APB=30?,
∴ OA=OP×sin∠APO=2×12=1,
∴ ⊙O的半径为1.
故选B.
4.
【答案】
C
【解答】
设三角形为△ABC,∠C=90?,AC=7,BC=24,
∴ AB=AC2+BC2=72+242=25,
设内切圆的半径为r,则S△ABC=12(AB+BC+CA)?r,
∴ 12AC?BC=12(AB+BC+CA)?r,即12×7×24=12×(7+24+25)?r,
解得r=3,
∴ 内切圆的直径是6步,
5.
【答案】
C
【解答】
解:∵ ∠BAC与∠BOC互补,
∴ ∠BAC+∠BOC=180?.
∵ ∠BAC=12∠BOC,
∴ ∠BOC=120?.
过O作OD⊥BC,垂足为D,
∴ BD=CD.
∵ OB=OC,
∴ OD平分∠BOC,
∴ ∠DOC=12∠BOC=60?,
∴ ∠OCD=90?-60?=30?.
在Rt△DOC中,OC=2,
∴ OD=1,
∴ DC=3,
∴ BC=2DC=23.
故选C.
6.
【答案】
A
【解答】
解:连接OA,
∵ PA切⊙O于A,
∴ ∠OAP=90?,
∴ 在Rt△OAP中,OP=10,OA=6,由勾股定理得:PA=8,
∵ PA,PB分别切⊙O于点A和点B,DE切⊙O于C,
∴ PA=PB=8,DA=DC,EB=EC,
∴ △PDE的周长是:
PD+DE+PE
=PD+DC+CE+PE
=PD+DA+EB+PE
=PA+PB
=8+8
=16,
故选A.
7.
【答案】
C
【解答】
解:∵ PT2=PA?PB,PT=4,PA=2,
∴ PB=8,
∴ AB=6,
故选C.
8.
【答案】
C
【解答】
解:∵ B、C分别是劣弧AD的三等分点,∠BOC=46?,
∴ ∠AOD=3×46?=138?,
∴ ∠AED=12∠AOD=138?÷2=69?(同弧所对的圆周角是所对的圆心角的一半).
故选C.
9.
【答案】
D
【解答】
解:∵ AB是⊙O的直径,AD切⊙O于点A,
∴ BA⊥DA,故A正确;
∵ EC=CB,
∴ ∠EAC=∠CAB,
∵ OA=OC,
∴ ∠CAB=∠ACO,
∴ ∠EAC=∠ACO,
∴ OC?//?AE,故B正确;
∵ ∠COE是CE所对的圆心角,∠CAE是CE所对的圆周角,
∴ ∠COE=2∠CAE,故C正确;
只有当AE=CE时OD⊥AC,故D错误.
故选D.
10.
【答案】
D
【解答】
∵ 点O是这段弧所在圆的圆心,
∴ OA=OB,
∵ ∠AOB=60?,
∴ △AOB是等边三角形,
∴ AB=OA=OB,
设AB=OB=OA=r,
∵ 点C是AB的中点,
∴ OC⊥AB,
∴ C,D,O三点共线,
∴ AD=DB=12rm,
在Rt△AOD中,
∴ OD=32r,
∵ OD+CD=OC,
∴ 32r+5=r,
解得:r=(20+103)m,
∴ 这段弯路的半径为(20+103)m
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
32
【解答】
∵ AB是⊙O的直径,
∴ ∠ACB=90?,
∴ ∠B=90?-∠BAC=90?-58?=32?,
∴ ∠D=∠B=32?.
12.
【答案】
75πcm2
【解答】
解:∵ 半径为5cm的圆的周长=10π,
∴ 10π=120πR180,解得R=15cm
∴ 扇形的面积=120π×152360=75πcm2.
故答案为:75πcm2.
13.
【答案】
140?
【解答】
解:∵ 四边形ABCD内接于⊙O,
∴ ∠C+∠A=180?,
∵ ∠C=110?,
∴ ∠A=70?,
∵ ∠BOD=2∠A,
∴ ∠BOD=140?.
故答案为:140?.
14.
【答案】
5
【解答】
解:
连接DO,且延长交AB于F,连接OE(E是切点),
∵ 在Rt△ABC中,∠B=90?,AB=6,BC=8,⊙O为△ABC的内切圆,
∴ 四边形OEBF、OEND是正方形,四边形BFDN是矩形,
∴ BE=BF=AB+AC-AB2=2,
∴ BN=4,
∴ N为BC的中点,
∵ MN?//?AB,
∴ M为AC的中点,
∴ MN=12AB=3,
∴ DM=3-2=1,
在Rt△ODM中,由勾股定理得:OM=22+12=5,
故答案为:5.
15.
【答案】
7
【解答】
解:∵ 弦AB、CD相交于点P,PA=2,PB=6,PC=3,
∴ PD=PA?PBPC=4.
∴ CD=7.
故答案为:7.
16.
【答案】
258
【解答】
解:如图连接CD、OD、OC,延长DO交AC于E,设半径为R.
在RT△ABC中,∵ ∠ACB=90?,BC=8,AC=6,
∴ AB=AC2+BC2=62+82=10,
∵ BD=AD=5,
∴ CD=AD=5,
∵ DC=DA,
CD=AD,
∴ DO⊥AC,EC=AE=3,
∴ ED?//?BC,∵ BD=AD,
∴ EC=EA,
∴ DE=12BC=4,
在RT△COE中,∵ ∠OEC=90?,
∴ CO2=OE2+CE2,
∴ R2=(4-R)2+32,
∴ R=258.
17.
【答案】
P是CD的中点
【解答】
解:根据垂径定理只要加上条件:P是CD的中点.(答案不唯一).
故答案是:P是CD的中点.
18.
【答案】
8
【解答】
解:∵ 直线PA、PB、MN分别与⊙O相切于点A、B、Q,
∴ MA=MQ,NQ=NB,
∴ △PMN的周长=PM+PN+MQ+NQ=PM+MA+PN+NM=PA+PB=4+4=8.
故答案为:8.
19.
【答案】
2
【解答】
解:设O是原正六边形的中心,连接AO,FO,MO,设FO与AE交于点Q,AO与BE交于P,
∵ 一个面积为6分米?2的正六边形,连接相隔一点的两顶点得到如图所示的对称图案,
∴ ∠AOF=16×360?=60?,S△AOF=16×6=1(分米?2),
∴ △OAF是等边三角形,
∵ AB=AF,
∴ OA⊥BF,
∴ AP=OP,
∴ AM=OM,
同理:OF⊥AE,OQ=FQ,
∴ OM=FM,
∴ 点M是△AOF的外心,
∴ S△OAM=13S△AOF=13(分米?2),
∴ S△OPM=12S△OAM=16(分米?2),
∴ 中间的正六边形的面积是:12×S△OPM=2(分米?2).
故答案为:2.
20.
【答案】
98π-324
【解答】
连接OC,过C作CE⊥OB于E,
∵ ∠AOB=90?,C是弧AB的中点,
∴ ∠AOC=∠BOC=45?,
∴ △OCE是等腰直角三角形,
∵ OD:OB=1:3,OA=3,
∴ CE=22×3=322,OD=1,
∴ 图中阴影部分的面积=S扇形COB-S△COD=45?π×32360-12×1×322=98π-324,
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
证明:∵ BC平分∠ABD,
∴ ∠OBC=∠DBC,
∵ 点C在圆上,OC为半径,
∴ OB=OC,
∴ ∠OBC=∠OCB,
∴ ∠OCB=∠DBC,
∴ OC?//?BD,
∵ BD⊥CD,
∴ OC⊥CD,
∴ CD为⊙O的切线.
【解答】
证明:∵ BC平分∠ABD,
∴ ∠OBC=∠DBC,
∵ 点C在圆上,OC为半径,
∴ OB=OC,
∴ ∠OBC=∠OCB,
∴ ∠OCB=∠DBC,
∴ OC?//?BD,
∵ BD⊥CD,
∴ OC⊥CD,
∴ CD为⊙O的切线.
22.
【答案】
解:直线DE与⊙O相切.理由如下:
过点O作AF交圆O于F点,连接BF.
∵ ∠F,∠C是同弧AB所对的角,
∴ ∠C=∠AFB,
∵ ∠BAE=∠C,
∴ ∠BAE=∠F,
∵ AF为直径,
∴ ∠ABF=90?,
∴ 在三角形ABF中,∠AFB+∠BAF=90?,
∵ ∠AFB=∠BAE,
∴ ∠BAE+∠BAF=90?,
∴ FA⊥DE,
∴ 直线DE与⊙O相切.
【解答】
解:直线DE与⊙O相切.理由如下:
过点O作AF交圆O于F点,连接BF.
∵ ∠F,∠C是同弧AB所对的角,
∴ ∠C=∠AFB,
∵ ∠BAE=∠C,
∴ ∠BAE=∠F,
∵ AF为直径,
∴ ∠ABF=90?,
∴ 在三角形ABF中,∠AFB+∠BAF=90?,
∵ ∠AFB=∠BAE,
∴ ∠BAE+∠BAF=90?,
∴ FA⊥DE,
∴ 直线DE与⊙O相切.
23.
【答案】
解:∵ ∠A=35?,
∴ ∠BOC=2∠A=70?,
∵ PC是⊙O的切线,
∴ OC⊥PC,
∴ ∠P=90?-∠BOC=20?.
【解答】
解:∵ ∠A=35?,
∴ ∠BOC=2∠A=70?,
∵ PC是⊙O的切线,
∴ OC⊥PC,
∴ ∠P=90?-∠BOC=20?.
24.
【答案】
解:(1)∵ △ABC中,∠ABC+∠ACB=180?-∠A=180?-72?=108?,
又∵ I是△ABC的内心,即∠IBC=12∠ABC,∠ICB=12∠ACB,
∴ ∠IBC+∠ICB=12×108?=54?,
∴ ∠BIC=180?-(∠IBC+∠ICB)=180?-54?=126?;
(2)∵ 点I是△ABC的外心,
∴ ∠BIC=2∠A=2×72?=144?.
【解答】
解:(1)∵ △ABC中,∠ABC+∠ACB=180?-∠A=180?-72?=108?,
又∵ I是△ABC的内心,即∠IBC=12∠ABC,∠ICB=12∠ACB,
∴ ∠IBC+∠ICB=12×108?=54?,
∴ ∠BIC=180?-(∠IBC+∠ICB)=180?-54?=126?;
(2)∵ 点I是△ABC的外心,
∴ ∠BIC=2∠A=2×72?=144?.
25.
【答案】
证明:如图,连接OA,
∵ CA=CB,
∴ CA=CB,
又∵ ∠ACB=120?,
∴ ∠B=30?,
∴ ∠O=2∠B=60?,
∵ ∠D=∠B=30?,
∴ ∠OAD=180?-(∠O+∠D)=90?,
∴ AD与⊙O相切;
∵ ∠O=60?,OA=OC,
∴ △OAC是等边三角形,
∴ ∠ACO=60?,
∵ ∠ACB=120?,
∴ ∠ACB=2∠ACO,AC=BC,
∴ OC⊥AB,AB=2BE,
∵ CE=4,∠B=30?,
∴ BC=2CE=8,
∴ BE=BC2-CE2=82-42=43,
∴ AB=2BE=83,
∴ 弦AB的长为83.
【解答】
证明:如图,连接OA,
∵ CA=CB,
∴ CA=CB,
又∵ ∠ACB=120?,
∴ ∠B=30?,
∴ ∠O=2∠B=60?,
∵ ∠D=∠B=30?,
∴ ∠OAD=180?-(∠O+∠D)=90?,
∴ AD与⊙O相切;
∵ ∠O=60?,OA=OC,
∴ △OAC是等边三角形,
∴ ∠ACO=60?,
∵ ∠ACB=120?,
∴ ∠ACB=2∠ACO,AC=BC,
∴ OC⊥AB,AB=2BE,
∵ CE=4,∠B=30?,
∴ BC=2CE=8,
∴ BE=BC2-CE2=82-42=43,
∴ AB=2BE=83,
∴ 弦AB的长为83.
(满分100分;时间:90分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 下列命题中,正确的个数是( )
(1)直径是弦,但弦不一定是直径;(2)半圆是弧,但弧不一定是半圆;
(3)半径相等的两个圆是等圆;(4)一条弦把圆分成的两段弧中,至少有一段是优弧.
A.1个 B.2个 C.3个 D.4个
?
2. 已知⊙O的半径为5,直线EF经过⊙O上一点P(点E,F在点P的两旁),下列条件能判定直线EF与⊙O相切的是( )
A.OP=5 B.OE=OF
C.O到直线EF的距离是4 D.OP⊥EF
?3. 如图,PA,PB为⊙O的切线,A,B分别为切点,∠APB=60?,点P到圆心O的距离OP=2,则⊙O的半径为(? ? ? ? )
A.12 B.1 C.32 D.2
?
4. 《九章算术》中“今有勾七步,股有二十四步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为7步,股(长直角边)长为24步,问该直角三角形的容圆(内切圆)直径是多少?”( )
A.4步 B.5步 C.6步 D.8步
?5. ⊙O的半径为2,△ABC是⊙O的内接三角形,连接OB,OC.若∠BAC与∠BOC互补,则弦BC的长为(? ? ? ? )
A.43 B.33 C.23 D.3
?
6. 如图,PA,PB分别切⊙O于点A和点B,C是AB上任一点,过C的切线分别交PA,PB于D,E.若⊙O的半径为6,PO=10,则△PDE的周长是( )
A.16 B.14 C.12 D.10
?
7. 如图,PT切⊙O于点T,经过圆心O的割线PAB交⊙O于点A、B,已知PT=4,PA=2,则⊙O的直径AB等于( )
A.3 B.4 C.6 D.8
?
8. 如图,已知点E是圆O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46?,则∠AED的度数为( )
A.138? B.46? C.69? D.92?
?9. 如图,已知AB是⊙O的直径,AD切⊙O于点A,EC=CB.则下列结论中不一定正确的是(? ? ? ? )
A.BA⊥DA B.OC?//?AE
C.∠COE=2∠CAE D.OD⊥AC
?10. 如图,一条公路的转弯处是一段圆弧(AB),点O是这段弧所在圆的圆心,∠AOB=60?,点C是AB的中点,且CD=5m,则这段弯路所在圆的半径为( )
A.(20-103)m B.20m C.30m D.(20+103)m
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
11. 如图,AB是⊙O的直径,点C、D是圆上位于AB两侧的点,若∠BAC=58?,则∠D=________??.
?
12. 已知扇形的圆心角为120?,弧长等于一个半径为5cm的圆的周长,则扇形的面积为________.
?
13. 如图,四边形ABCD内接于⊙O,∠C=110?,连接OB、OD,则∠BOD=________.
?
14. 如图,在Rt△ABC中,∠B=90?,AB=6,BC=8,⊙O为△ABC的内切圆,M、N分别在边AC、BC上,且MN?//?AB,MN切⊙O于D点,则MO=________.
?
15. 已知:如图,在⊙O中,弦AB、CD相交于点P,PA=2,PB=6,PC=3,则CD=________.
?
16. 如图,直角△ABC的直角顶点C,另一顶点A及斜边AB的中点D都在⊙O上,已知:AC=6,BC=8,则⊙O的半径为________.
?
17. 如图,⊙O的直径AB与弦CD交于点P,添加条件________(写出一个即可),就可得到点P是CD的中点. ?
18. 如图,PA、PB是⊙O的切线,Q为AB上一点,过点Q的直线MN与⊙O相切,已知PA=4,则△PMN周长=________.
?
19. 小刚在纸上画了一个面积为6分米?2的正六边形,然后连接相隔一点的两点得到如图所示的对称图案,他发现中间也出现了一个正六边形,则中间的正六边形的面积是________分米?2.
?
20. 如图,在扇形ABO中,∠AOB=90?,C是弧AB的中点,若OD:OB=1:3,OA=3,则图中阴影部分的面积为________.
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
21. 如图所示,AB是⊙O的直径,点C为⊙O上一点,过点B作BD⊥CD,垂足为点D,连结BC,BC平分∠ABD.
求证:CD为⊙O的切线.
?
22. 已知:如图,△ABC内接于⊙O,过A点作直线DE,当∠BAE=∠C时,试确定直线DE与⊙O的位置关系,并证明你的结论.
?
23. 如图,已知AB是⊙O的直径,P为AB延长线上的一点,PC是⊙O的切线,C为切点,∠A=35?,求∠P的度数.
?
24. 如图,在△ABC中,∠A=72?,点I是△ABC内的一点.
(1)若点I是△ABC的内心,求∠BIC的度数;
(2)若点I是△ABC的外心,求∠BIC的度数.
?
25. 如图,在⊙O中,点C为AB的中点,∠ACB=120?,OC的延长线与AD交于点D,且∠D=∠B.
(1)求证:AD与⊙O相切;
(2)若CE=4,求弦AB的长.
?
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
【解答】
解:当弦为直径时,不会把圆分成一段优弧一段劣弧,
∴ (4)为假命题
而(1)、(2)、(3)均正确
故选C.
2.
【答案】
D
【解答】
∵ 点P在⊙O上,
∴ 只需要OP⊥EF即可,
3.
【答案】
B
【解答】
解:如图,连接OA,OB,
∵ PA,PB为⊙O的切线交于点P,
∴ PA⊥OA,PB⊥OB,OA=OB.
由角平分线定义可知:∠APO=12∠APB=30?,
∴ OA=OP×sin∠APO=2×12=1,
∴ ⊙O的半径为1.
故选B.
4.
【答案】
C
【解答】
设三角形为△ABC,∠C=90?,AC=7,BC=24,
∴ AB=AC2+BC2=72+242=25,
设内切圆的半径为r,则S△ABC=12(AB+BC+CA)?r,
∴ 12AC?BC=12(AB+BC+CA)?r,即12×7×24=12×(7+24+25)?r,
解得r=3,
∴ 内切圆的直径是6步,
5.
【答案】
C
【解答】
解:∵ ∠BAC与∠BOC互补,
∴ ∠BAC+∠BOC=180?.
∵ ∠BAC=12∠BOC,
∴ ∠BOC=120?.
过O作OD⊥BC,垂足为D,
∴ BD=CD.
∵ OB=OC,
∴ OD平分∠BOC,
∴ ∠DOC=12∠BOC=60?,
∴ ∠OCD=90?-60?=30?.
在Rt△DOC中,OC=2,
∴ OD=1,
∴ DC=3,
∴ BC=2DC=23.
故选C.
6.
【答案】
A
【解答】
解:连接OA,
∵ PA切⊙O于A,
∴ ∠OAP=90?,
∴ 在Rt△OAP中,OP=10,OA=6,由勾股定理得:PA=8,
∵ PA,PB分别切⊙O于点A和点B,DE切⊙O于C,
∴ PA=PB=8,DA=DC,EB=EC,
∴ △PDE的周长是:
PD+DE+PE
=PD+DC+CE+PE
=PD+DA+EB+PE
=PA+PB
=8+8
=16,
故选A.
7.
【答案】
C
【解答】
解:∵ PT2=PA?PB,PT=4,PA=2,
∴ PB=8,
∴ AB=6,
故选C.
8.
【答案】
C
【解答】
解:∵ B、C分别是劣弧AD的三等分点,∠BOC=46?,
∴ ∠AOD=3×46?=138?,
∴ ∠AED=12∠AOD=138?÷2=69?(同弧所对的圆周角是所对的圆心角的一半).
故选C.
9.
【答案】
D
【解答】
解:∵ AB是⊙O的直径,AD切⊙O于点A,
∴ BA⊥DA,故A正确;
∵ EC=CB,
∴ ∠EAC=∠CAB,
∵ OA=OC,
∴ ∠CAB=∠ACO,
∴ ∠EAC=∠ACO,
∴ OC?//?AE,故B正确;
∵ ∠COE是CE所对的圆心角,∠CAE是CE所对的圆周角,
∴ ∠COE=2∠CAE,故C正确;
只有当AE=CE时OD⊥AC,故D错误.
故选D.
10.
【答案】
D
【解答】
∵ 点O是这段弧所在圆的圆心,
∴ OA=OB,
∵ ∠AOB=60?,
∴ △AOB是等边三角形,
∴ AB=OA=OB,
设AB=OB=OA=r,
∵ 点C是AB的中点,
∴ OC⊥AB,
∴ C,D,O三点共线,
∴ AD=DB=12rm,
在Rt△AOD中,
∴ OD=32r,
∵ OD+CD=OC,
∴ 32r+5=r,
解得:r=(20+103)m,
∴ 这段弯路的半径为(20+103)m
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
32
【解答】
∵ AB是⊙O的直径,
∴ ∠ACB=90?,
∴ ∠B=90?-∠BAC=90?-58?=32?,
∴ ∠D=∠B=32?.
12.
【答案】
75πcm2
【解答】
解:∵ 半径为5cm的圆的周长=10π,
∴ 10π=120πR180,解得R=15cm
∴ 扇形的面积=120π×152360=75πcm2.
故答案为:75πcm2.
13.
【答案】
140?
【解答】
解:∵ 四边形ABCD内接于⊙O,
∴ ∠C+∠A=180?,
∵ ∠C=110?,
∴ ∠A=70?,
∵ ∠BOD=2∠A,
∴ ∠BOD=140?.
故答案为:140?.
14.
【答案】
5
【解答】
解:
连接DO,且延长交AB于F,连接OE(E是切点),
∵ 在Rt△ABC中,∠B=90?,AB=6,BC=8,⊙O为△ABC的内切圆,
∴ 四边形OEBF、OEND是正方形,四边形BFDN是矩形,
∴ BE=BF=AB+AC-AB2=2,
∴ BN=4,
∴ N为BC的中点,
∵ MN?//?AB,
∴ M为AC的中点,
∴ MN=12AB=3,
∴ DM=3-2=1,
在Rt△ODM中,由勾股定理得:OM=22+12=5,
故答案为:5.
15.
【答案】
7
【解答】
解:∵ 弦AB、CD相交于点P,PA=2,PB=6,PC=3,
∴ PD=PA?PBPC=4.
∴ CD=7.
故答案为:7.
16.
【答案】
258
【解答】
解:如图连接CD、OD、OC,延长DO交AC于E,设半径为R.
在RT△ABC中,∵ ∠ACB=90?,BC=8,AC=6,
∴ AB=AC2+BC2=62+82=10,
∵ BD=AD=5,
∴ CD=AD=5,
∵ DC=DA,
CD=AD,
∴ DO⊥AC,EC=AE=3,
∴ ED?//?BC,∵ BD=AD,
∴ EC=EA,
∴ DE=12BC=4,
在RT△COE中,∵ ∠OEC=90?,
∴ CO2=OE2+CE2,
∴ R2=(4-R)2+32,
∴ R=258.
17.
【答案】
P是CD的中点
【解答】
解:根据垂径定理只要加上条件:P是CD的中点.(答案不唯一).
故答案是:P是CD的中点.
18.
【答案】
8
【解答】
解:∵ 直线PA、PB、MN分别与⊙O相切于点A、B、Q,
∴ MA=MQ,NQ=NB,
∴ △PMN的周长=PM+PN+MQ+NQ=PM+MA+PN+NM=PA+PB=4+4=8.
故答案为:8.
19.
【答案】
2
【解答】
解:设O是原正六边形的中心,连接AO,FO,MO,设FO与AE交于点Q,AO与BE交于P,
∵ 一个面积为6分米?2的正六边形,连接相隔一点的两顶点得到如图所示的对称图案,
∴ ∠AOF=16×360?=60?,S△AOF=16×6=1(分米?2),
∴ △OAF是等边三角形,
∵ AB=AF,
∴ OA⊥BF,
∴ AP=OP,
∴ AM=OM,
同理:OF⊥AE,OQ=FQ,
∴ OM=FM,
∴ 点M是△AOF的外心,
∴ S△OAM=13S△AOF=13(分米?2),
∴ S△OPM=12S△OAM=16(分米?2),
∴ 中间的正六边形的面积是:12×S△OPM=2(分米?2).
故答案为:2.
20.
【答案】
98π-324
【解答】
连接OC,过C作CE⊥OB于E,
∵ ∠AOB=90?,C是弧AB的中点,
∴ ∠AOC=∠BOC=45?,
∴ △OCE是等腰直角三角形,
∵ OD:OB=1:3,OA=3,
∴ CE=22×3=322,OD=1,
∴ 图中阴影部分的面积=S扇形COB-S△COD=45?π×32360-12×1×322=98π-324,
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
证明:∵ BC平分∠ABD,
∴ ∠OBC=∠DBC,
∵ 点C在圆上,OC为半径,
∴ OB=OC,
∴ ∠OBC=∠OCB,
∴ ∠OCB=∠DBC,
∴ OC?//?BD,
∵ BD⊥CD,
∴ OC⊥CD,
∴ CD为⊙O的切线.
【解答】
证明:∵ BC平分∠ABD,
∴ ∠OBC=∠DBC,
∵ 点C在圆上,OC为半径,
∴ OB=OC,
∴ ∠OBC=∠OCB,
∴ ∠OCB=∠DBC,
∴ OC?//?BD,
∵ BD⊥CD,
∴ OC⊥CD,
∴ CD为⊙O的切线.
22.
【答案】
解:直线DE与⊙O相切.理由如下:
过点O作AF交圆O于F点,连接BF.
∵ ∠F,∠C是同弧AB所对的角,
∴ ∠C=∠AFB,
∵ ∠BAE=∠C,
∴ ∠BAE=∠F,
∵ AF为直径,
∴ ∠ABF=90?,
∴ 在三角形ABF中,∠AFB+∠BAF=90?,
∵ ∠AFB=∠BAE,
∴ ∠BAE+∠BAF=90?,
∴ FA⊥DE,
∴ 直线DE与⊙O相切.
【解答】
解:直线DE与⊙O相切.理由如下:
过点O作AF交圆O于F点,连接BF.
∵ ∠F,∠C是同弧AB所对的角,
∴ ∠C=∠AFB,
∵ ∠BAE=∠C,
∴ ∠BAE=∠F,
∵ AF为直径,
∴ ∠ABF=90?,
∴ 在三角形ABF中,∠AFB+∠BAF=90?,
∵ ∠AFB=∠BAE,
∴ ∠BAE+∠BAF=90?,
∴ FA⊥DE,
∴ 直线DE与⊙O相切.
23.
【答案】
解:∵ ∠A=35?,
∴ ∠BOC=2∠A=70?,
∵ PC是⊙O的切线,
∴ OC⊥PC,
∴ ∠P=90?-∠BOC=20?.
【解答】
解:∵ ∠A=35?,
∴ ∠BOC=2∠A=70?,
∵ PC是⊙O的切线,
∴ OC⊥PC,
∴ ∠P=90?-∠BOC=20?.
24.
【答案】
解:(1)∵ △ABC中,∠ABC+∠ACB=180?-∠A=180?-72?=108?,
又∵ I是△ABC的内心,即∠IBC=12∠ABC,∠ICB=12∠ACB,
∴ ∠IBC+∠ICB=12×108?=54?,
∴ ∠BIC=180?-(∠IBC+∠ICB)=180?-54?=126?;
(2)∵ 点I是△ABC的外心,
∴ ∠BIC=2∠A=2×72?=144?.
【解答】
解:(1)∵ △ABC中,∠ABC+∠ACB=180?-∠A=180?-72?=108?,
又∵ I是△ABC的内心,即∠IBC=12∠ABC,∠ICB=12∠ACB,
∴ ∠IBC+∠ICB=12×108?=54?,
∴ ∠BIC=180?-(∠IBC+∠ICB)=180?-54?=126?;
(2)∵ 点I是△ABC的外心,
∴ ∠BIC=2∠A=2×72?=144?.
25.
【答案】
证明:如图,连接OA,
∵ CA=CB,
∴ CA=CB,
又∵ ∠ACB=120?,
∴ ∠B=30?,
∴ ∠O=2∠B=60?,
∵ ∠D=∠B=30?,
∴ ∠OAD=180?-(∠O+∠D)=90?,
∴ AD与⊙O相切;
∵ ∠O=60?,OA=OC,
∴ △OAC是等边三角形,
∴ ∠ACO=60?,
∵ ∠ACB=120?,
∴ ∠ACB=2∠ACO,AC=BC,
∴ OC⊥AB,AB=2BE,
∵ CE=4,∠B=30?,
∴ BC=2CE=8,
∴ BE=BC2-CE2=82-42=43,
∴ AB=2BE=83,
∴ 弦AB的长为83.
【解答】
证明:如图,连接OA,
∵ CA=CB,
∴ CA=CB,
又∵ ∠ACB=120?,
∴ ∠B=30?,
∴ ∠O=2∠B=60?,
∵ ∠D=∠B=30?,
∴ ∠OAD=180?-(∠O+∠D)=90?,
∴ AD与⊙O相切;
∵ ∠O=60?,OA=OC,
∴ △OAC是等边三角形,
∴ ∠ACO=60?,
∵ ∠ACB=120?,
∴ ∠ACB=2∠ACO,AC=BC,
∴ OC⊥AB,AB=2BE,
∵ CE=4,∠B=30?,
∴ BC=2CE=8,
∴ BE=BC2-CE2=82-42=43,
∴ AB=2BE=83,
∴ 弦AB的长为83.
