27.2.1第3课相似三角形的判定(2) 课件(共26张PPT)
文档属性
| 名称 | 27.2.1第3课相似三角形的判定(2) 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 00:00:00 | ||
图片预览



文档简介
27.2.1 相似三角形的判定
第3课时 相似三角形的判定(2)
人教版数学九年级下册
第二十七章 相似
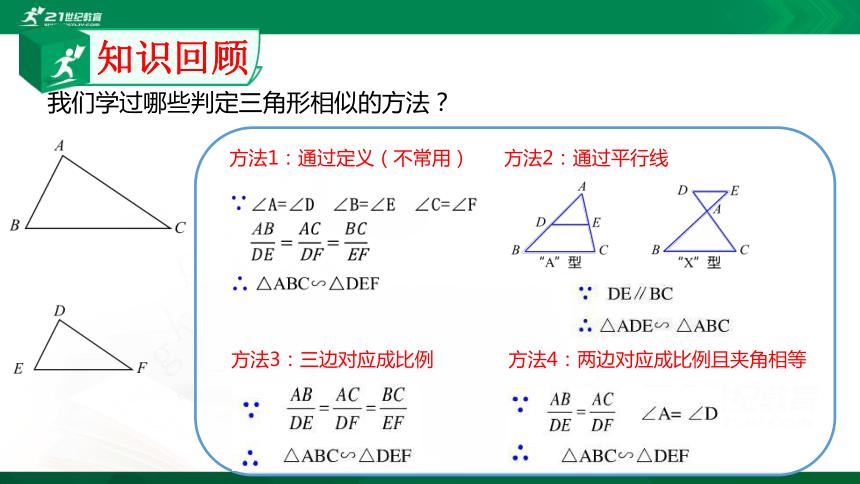
我们学过哪些判定三角形相似的方法?
方法1:通过定义(不常用)
方法2:通过平行线
方法3:三边对应成比例
方法4:两边对应成比例且夹角相等
知识回顾
1
探索两角分别相等的两个三角形相似的判定定理.
2
掌握利用两角来判定两个三角形相似的方法,并能进行相关计算. (重点、难点)
3
掌握判定两个直角三角形相似的方法,并能进行相关计算.
学习目标
A
B
C
C'
B'
A'
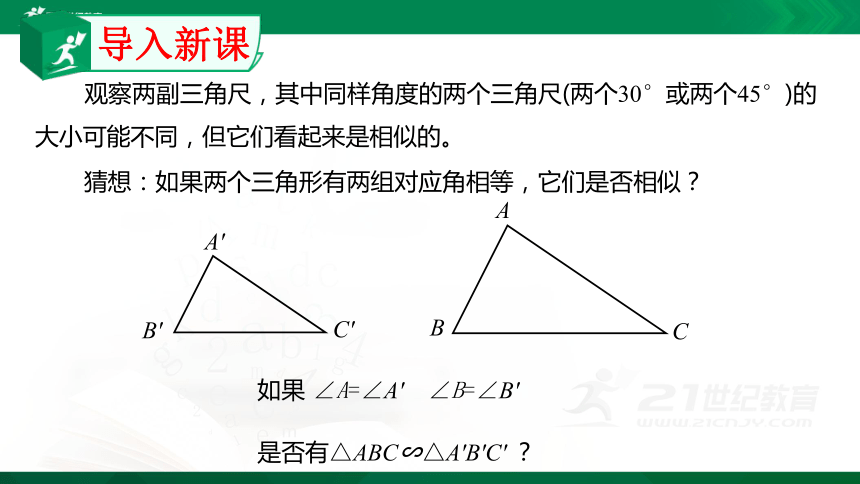
是否有△ABC∽△A'B'C' ?
如果 ∠A=∠A' ∠B=∠B'
观察两副三角尺,其中同样角度的两个三角尺(两个30°或两个45°)的大小可能不同,但它们看起来是相似的。
猜想:如果两个三角形有两组对应角相等,它们是否相似?
导入新课
一、相似三角形的判定(AA)
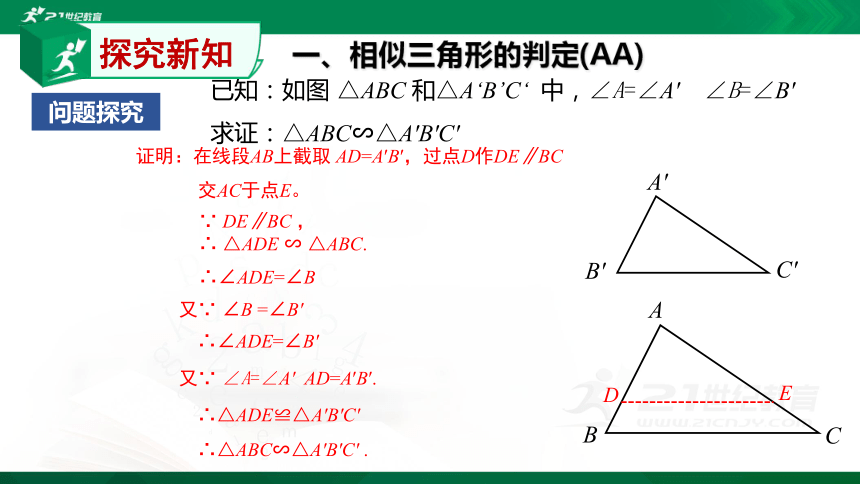
已知:如图 △ABC 和△A‘B’C‘ 中,∠A=∠A' ∠B=∠B'
求证:△ABC∽△A'B'C'
问题探究
A
B
C
C'
B'
A'
D
E
∴∠ADE=∠B
证明:在线段AB上截取 AD=A′B′,过点D作DE∥BC
交AC于点E。
∵ DE∥BC ,
∴ △ADE ∽ △ABC.
又∵ ∠A=∠A' AD=A′B′.
∴△ADE≌△A′B′C′
∴△ABC∽△A′B′C′ .
又∵ ∠B =∠B'
∴∠ADE=∠B'
探究新知
一、相似三角形的判定(AA)
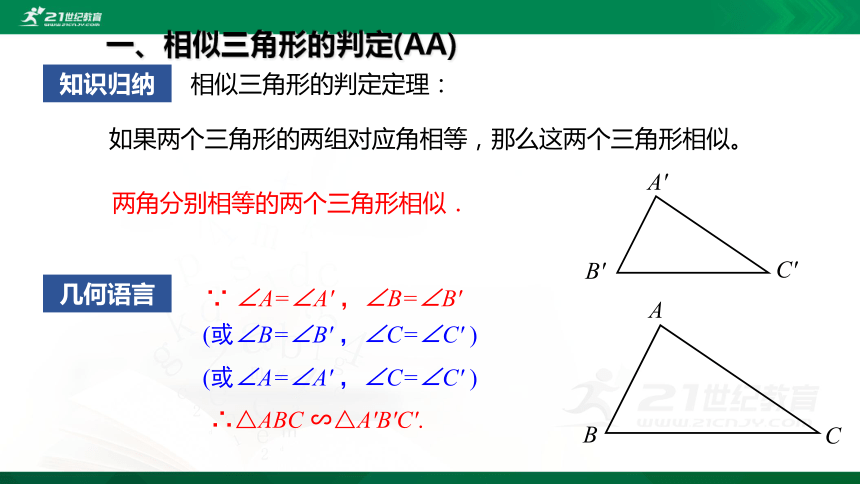
相似三角形的判定定理:
知识归纳
几何语言
如果两个三角形的两组对应角相等,那么这两个三角形相似。
两角分别相等的两个三角形相似.
A
B
C
C'
B'
A'
∴△ABC ∽△A′B′C′.
∵ ∠A=∠A′ ,∠B=∠B′
(或∠B=∠B′ ,∠C=∠C′ )
(或∠A=∠A′ ,∠C=∠C′ )
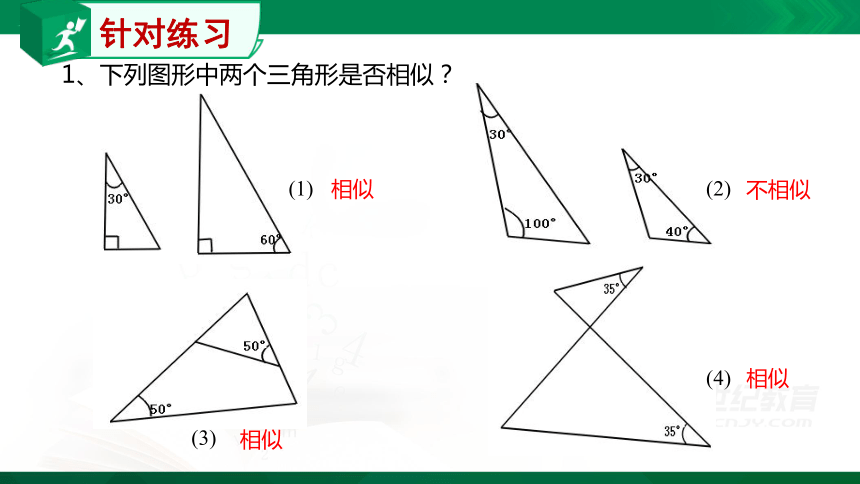
1、下列图形中两个三角形是否相似?
(1)
(2)
(3)
(4)
相似
不相似
相似
相似
针对练习
2、根据下列条件,判断 △ABC 和 △A’B’C’ 是否相似,并说明理由:
(1) ∠A=35°, AB=12cm, AC=15cm,
∠A'=35°, A'B'=36cm, A'C'=45cm,
(2) AB=12cm, BC=15cm, AC=24cm,
A'B'=20cm, B'C'=25cm, A'C'=40cm.
(3) ∠A=105°, ∠B=15°;
∠A'=105°, ∠B'=15°
∠B'=60°
相似,(SAS)
相似,(SSS)
相似,(AA)
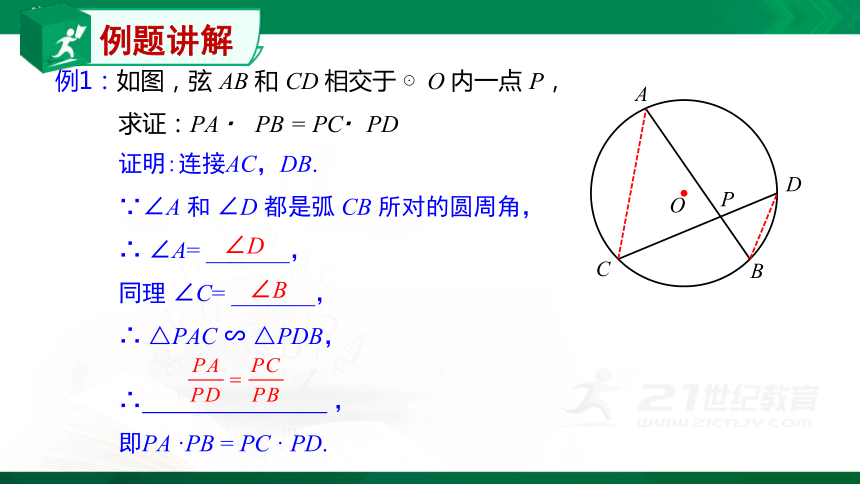
例1:如图,弦 AB 和 CD 相交于 ⊙O 内一点 P,
求证:PA ? PB = PC?PD
A
B
C
D
P
O
证明:连接AC,DB.
∵∠A 和 ∠D 都是弧 CB 所对的圆周角,
∴ ∠A= _______,
同理 ∠C= _______,
∴ △PAC ∽ △PDB,
∴ ,
即PA ·PB = PC · PD.
∠D
∠B
例题讲解
1. 如果弦 AB 和 CD 相交于 ⊙O 外一点 P,那么PA ? PB = PC?PD吗?
A
B
C
D
P
O
2. 如果上题中A、B两点重合,又会有什么结论?
A
(B)
C
D
P
O
PA2= PC?PD
分析:连接AC,DB.
证 △PAC ∽ △PDB
针对练习
∴
解:∵ ED⊥AB,∴∠EDA=90 ° .
又∵ ∠C=90 °,∠A=∠A,
∴ △AED ∽△ABC.
例2: 如图,在 Rt△ABC 中,∠C = 90°,AB = 10,AC = 8. E 是 AC 上一点,AE = 5,ED⊥AB,垂足为 D. 求 AD 的长.
D
A
B
C
E
∴
有一个锐角相等的两个直角三角形相似.
归纳
例题讲解
二、直角三角形相似的判定(HL)
是否有Rt△ABC∽ Rt △A'B'C' ?
如果∠C=∠C′ =90°,
类比判定直角三角形全等的“HL”方法,
我们能不能通过斜边和一组直角边成比例来判定两个直角三角形相似呢?
A
B
C
C′
B′
A′
二、直角三角形相似的判定(HL)
已知:如图 Rt △ABC 和Rt △A'B'C' 中
∠C=∠C′ =90°,
求证: Rt △ABC∽ Rt △A'B'C'
问题探究
D
E
A
B
C
C′
B′
A′
证明:在线段AB上截取 AD=A′B′,过点D作DE∥BC交AC于点E。
∵ DE∥BC ,
∴ △ADE ∽ △ABC,∠AED =∠C =90°
∴ AE = A′C′.
∴ Rt△ADE ≌ Rt△A′B′C′
∴ Rt△ABC ∽ Rt△A′B′C′ .
∴ ,∠AED =∠C ′ =90°
?
又∵ ,且AD = A′B′,
?
二、直角三角形相似的判定(HL)
直角三角形相似的判定定理:
知识归纳
几何语言
如果两个直角三角形的斜边和一组直角边的比相等,那么这两个直角三角形相似。
斜边和一直角边成比例的两个直角三角形相似.
∴Rt△ABC ∽ Rt△A′B′C′.
∵∠C=∠C′ =90°,
?
A
B
C
C′
B′
A′
在 Rt△ABC 和 Rt△A′B′C′ 中,∠C=∠C′=90°,依据下列各组条
件判定这两个三角形是否相似.
(1) ∠A=35°,∠B′=55°;
(2) AC=3,BC=4,A′C′=6,B′C′=8;
(3) AB=10,AC=8,A′B′=25,B′C′=15。
相似
相似
相似
针对练习
例3:如图,已知:∠ACB =∠ADC = 90°,AD = 2,CD = ,
当 AB 的长为 时,△ACB 与△ADC 相似.
C
A
B
D
3 或
解析:∵∠ADC = 90°,AD = 2,CD = ,
∴
(1) 当 Rt△ABC ∽ Rt△ACD 时,
有 AC : AD=AB : AC,
即 ,
解得 AB=3;
?
(2) 当 Rt△ABC ∽ Rt△ADC 时,
有 AC : CD=AB : AC,
即 ,
解得 AB= ;
?
?
∴ 当 AB 的长为 3 或 时,这两个直角三角形相似.
?
例题讲解
例4:求证:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。
已知:在Rt△ABC中,CD 是斜边AB 上的高。
此结论可以称为“母子相似定理”,或“射影定理”
求证: △ABC∽△ACD∽△CBD
结论: △ACD∽ △CBD CD2=AD · DB
△ACD∽ △ABC AC2=AD · AB
△BCD∽ △ABC BC2=BD · AB
A
D
B
C
例题讲解
定义法
判定定理
相似三角形的判定
平行法
比较复杂,烦琐.
有局限性,只能在特定的图形里面使用.
两边成比例且夹角相等的两个三角形相似.
两角分别相等的两个三角形相似.
三边成比例的两个三角形相似.
斜边和一直角边成比例的两个直角三角形相似.
课堂小结
1. 如图,△ABC中,AE 交 BC 于点 D,∠C=∠E,AD : DE=3 : 5,AE=8,BD=4,则DC 的长等于 ( )
A.
B.
C.
D.
A
C
A
B
D
E
课堂练习
2. 如图,在Rt△ABC 中,∠ABC=90°, BD⊥AC 于 D ,若 AB = 6,
AD = 2,则AC = ,BD = ,BC = 。
18
A
D
B
C
?
?
证明: ∵ △ABC 的高AD、BE交于点F,
∴ ∠FEA=∠FDB=90°,
∠AFE =∠BFD (对顶角相等).
∴ △FEA ∽ △ FDB,
∴
3. 如图,△ABC 的高 AD、BE 交于点 F.
求证:
D
C
A
B
E
F
证明:
∵∠BAC =∠1+∠DAC,
∠DAE =∠3+∠DAC,∠1=∠3,
∴∠BAC =∠DAE.
∵∠C =180°-∠2-∠DOC ,
∠E =180°-∠3-∠AOE,
∠DOC =∠AOE(对顶角相等),
∴∠C = ∠E.
∴ △ABC∽△ADE.
4. 如图,∠1=∠2=∠3,求证:△ABC ∽△ADE.
A
B
C
D
E
1
3
2
O
5. 如图,直线 BE、DC 交于A , AD·AC = AE·BA,
求证:∠E=∠C
E
D
B
C
A
A
B
C
E
D
如何证明∠AED=∠C?
A
B
C
D
解: ∵ ∠ A= ∠ A ∠ABD=∠C
∴ △ABD ∽ △ACB
∴ AB : AC=AD : AB
∴ AB2 = AD · AC
∵ AD=2 AC=8
∴ AB =4
6. 已知如图,∠ABD=∠C ,AD=2 ,AC=8,求AB
A
B
C
D
第3课时 相似三角形的判定(2)
人教版数学九年级下册
第二十七章 相似
我们学过哪些判定三角形相似的方法?
方法1:通过定义(不常用)
方法2:通过平行线
方法3:三边对应成比例
方法4:两边对应成比例且夹角相等
知识回顾
1
探索两角分别相等的两个三角形相似的判定定理.
2
掌握利用两角来判定两个三角形相似的方法,并能进行相关计算. (重点、难点)
3
掌握判定两个直角三角形相似的方法,并能进行相关计算.
学习目标
A
B
C
C'
B'
A'
是否有△ABC∽△A'B'C' ?
如果 ∠A=∠A' ∠B=∠B'
观察两副三角尺,其中同样角度的两个三角尺(两个30°或两个45°)的大小可能不同,但它们看起来是相似的。
猜想:如果两个三角形有两组对应角相等,它们是否相似?
导入新课
一、相似三角形的判定(AA)
已知:如图 △ABC 和△A‘B’C‘ 中,∠A=∠A' ∠B=∠B'
求证:△ABC∽△A'B'C'
问题探究
A
B
C
C'
B'
A'
D
E
∴∠ADE=∠B
证明:在线段AB上截取 AD=A′B′,过点D作DE∥BC
交AC于点E。
∵ DE∥BC ,
∴ △ADE ∽ △ABC.
又∵ ∠A=∠A' AD=A′B′.
∴△ADE≌△A′B′C′
∴△ABC∽△A′B′C′ .
又∵ ∠B =∠B'
∴∠ADE=∠B'
探究新知
一、相似三角形的判定(AA)
相似三角形的判定定理:
知识归纳
几何语言
如果两个三角形的两组对应角相等,那么这两个三角形相似。
两角分别相等的两个三角形相似.
A
B
C
C'
B'
A'
∴△ABC ∽△A′B′C′.
∵ ∠A=∠A′ ,∠B=∠B′
(或∠B=∠B′ ,∠C=∠C′ )
(或∠A=∠A′ ,∠C=∠C′ )
1、下列图形中两个三角形是否相似?
(1)
(2)
(3)
(4)
相似
不相似
相似
相似
针对练习
2、根据下列条件,判断 △ABC 和 △A’B’C’ 是否相似,并说明理由:
(1) ∠A=35°, AB=12cm, AC=15cm,
∠A'=35°, A'B'=36cm, A'C'=45cm,
(2) AB=12cm, BC=15cm, AC=24cm,
A'B'=20cm, B'C'=25cm, A'C'=40cm.
(3) ∠A=105°, ∠B=15°;
∠A'=105°, ∠B'=15°
∠B'=60°
相似,(SAS)
相似,(SSS)
相似,(AA)
例1:如图,弦 AB 和 CD 相交于 ⊙O 内一点 P,
求证:PA ? PB = PC?PD
A
B
C
D
P
O
证明:连接AC,DB.
∵∠A 和 ∠D 都是弧 CB 所对的圆周角,
∴ ∠A= _______,
同理 ∠C= _______,
∴ △PAC ∽ △PDB,
∴ ,
即PA ·PB = PC · PD.
∠D
∠B
例题讲解
1. 如果弦 AB 和 CD 相交于 ⊙O 外一点 P,那么PA ? PB = PC?PD吗?
A
B
C
D
P
O
2. 如果上题中A、B两点重合,又会有什么结论?
A
(B)
C
D
P
O
PA2= PC?PD
分析:连接AC,DB.
证 △PAC ∽ △PDB
针对练习
∴
解:∵ ED⊥AB,∴∠EDA=90 ° .
又∵ ∠C=90 °,∠A=∠A,
∴ △AED ∽△ABC.
例2: 如图,在 Rt△ABC 中,∠C = 90°,AB = 10,AC = 8. E 是 AC 上一点,AE = 5,ED⊥AB,垂足为 D. 求 AD 的长.
D
A
B
C
E
∴
有一个锐角相等的两个直角三角形相似.
归纳
例题讲解
二、直角三角形相似的判定(HL)
是否有Rt△ABC∽ Rt △A'B'C' ?
如果∠C=∠C′ =90°,
类比判定直角三角形全等的“HL”方法,
我们能不能通过斜边和一组直角边成比例来判定两个直角三角形相似呢?
A
B
C
C′
B′
A′
二、直角三角形相似的判定(HL)
已知:如图 Rt △ABC 和Rt △A'B'C' 中
∠C=∠C′ =90°,
求证: Rt △ABC∽ Rt △A'B'C'
问题探究
D
E
A
B
C
C′
B′
A′
证明:在线段AB上截取 AD=A′B′,过点D作DE∥BC交AC于点E。
∵ DE∥BC ,
∴ △ADE ∽ △ABC,∠AED =∠C =90°
∴ AE = A′C′.
∴ Rt△ADE ≌ Rt△A′B′C′
∴ Rt△ABC ∽ Rt△A′B′C′ .
∴ ,∠AED =∠C ′ =90°
?
又∵ ,且AD = A′B′,
?
二、直角三角形相似的判定(HL)
直角三角形相似的判定定理:
知识归纳
几何语言
如果两个直角三角形的斜边和一组直角边的比相等,那么这两个直角三角形相似。
斜边和一直角边成比例的两个直角三角形相似.
∴Rt△ABC ∽ Rt△A′B′C′.
∵∠C=∠C′ =90°,
?
A
B
C
C′
B′
A′
在 Rt△ABC 和 Rt△A′B′C′ 中,∠C=∠C′=90°,依据下列各组条
件判定这两个三角形是否相似.
(1) ∠A=35°,∠B′=55°;
(2) AC=3,BC=4,A′C′=6,B′C′=8;
(3) AB=10,AC=8,A′B′=25,B′C′=15。
相似
相似
相似
针对练习
例3:如图,已知:∠ACB =∠ADC = 90°,AD = 2,CD = ,
当 AB 的长为 时,△ACB 与△ADC 相似.
C
A
B
D
3 或
解析:∵∠ADC = 90°,AD = 2,CD = ,
∴
(1) 当 Rt△ABC ∽ Rt△ACD 时,
有 AC : AD=AB : AC,
即 ,
解得 AB=3;
?
(2) 当 Rt△ABC ∽ Rt△ADC 时,
有 AC : CD=AB : AC,
即 ,
解得 AB= ;
?
?
∴ 当 AB 的长为 3 或 时,这两个直角三角形相似.
?
例题讲解
例4:求证:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。
已知:在Rt△ABC中,CD 是斜边AB 上的高。
此结论可以称为“母子相似定理”,或“射影定理”
求证: △ABC∽△ACD∽△CBD
结论: △ACD∽ △CBD CD2=AD · DB
△ACD∽ △ABC AC2=AD · AB
△BCD∽ △ABC BC2=BD · AB
A
D
B
C
例题讲解
定义法
判定定理
相似三角形的判定
平行法
比较复杂,烦琐.
有局限性,只能在特定的图形里面使用.
两边成比例且夹角相等的两个三角形相似.
两角分别相等的两个三角形相似.
三边成比例的两个三角形相似.
斜边和一直角边成比例的两个直角三角形相似.
课堂小结
1. 如图,△ABC中,AE 交 BC 于点 D,∠C=∠E,AD : DE=3 : 5,AE=8,BD=4,则DC 的长等于 ( )
A.
B.
C.
D.
A
C
A
B
D
E
课堂练习
2. 如图,在Rt△ABC 中,∠ABC=90°, BD⊥AC 于 D ,若 AB = 6,
AD = 2,则AC = ,BD = ,BC = 。
18
A
D
B
C
?
?
证明: ∵ △ABC 的高AD、BE交于点F,
∴ ∠FEA=∠FDB=90°,
∠AFE =∠BFD (对顶角相等).
∴ △FEA ∽ △ FDB,
∴
3. 如图,△ABC 的高 AD、BE 交于点 F.
求证:
D
C
A
B
E
F
证明:
∵∠BAC =∠1+∠DAC,
∠DAE =∠3+∠DAC,∠1=∠3,
∴∠BAC =∠DAE.
∵∠C =180°-∠2-∠DOC ,
∠E =180°-∠3-∠AOE,
∠DOC =∠AOE(对顶角相等),
∴∠C = ∠E.
∴ △ABC∽△ADE.
4. 如图,∠1=∠2=∠3,求证:△ABC ∽△ADE.
A
B
C
D
E
1
3
2
O
5. 如图,直线 BE、DC 交于A , AD·AC = AE·BA,
求证:∠E=∠C
E
D
B
C
A
A
B
C
E
D
如何证明∠AED=∠C?
A
B
C
D
解: ∵ ∠ A= ∠ A ∠ABD=∠C
∴ △ABD ∽ △ACB
∴ AB : AC=AD : AB
∴ AB2 = AD · AC
∵ AD=2 AC=8
∴ AB =4
6. 已知如图,∠ABD=∠C ,AD=2 ,AC=8,求AB
A
B
C
D
