七年级数学一元一次方程的应用--行程问题
文档属性
| 名称 | 七年级数学一元一次方程的应用--行程问题 |

|
|
| 格式 | rar | ||
| 文件大小 | 268.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-07 00:00:00 | ||
图片预览


文档简介
(共9张PPT)
一元一次方程的应用
之
“行程问题”
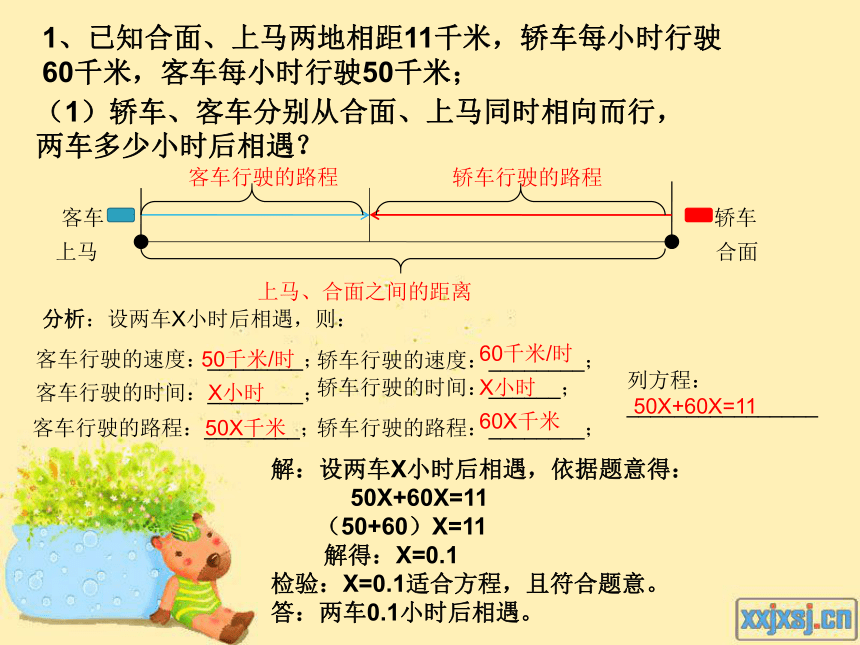
1、已知合面、上马两地相距11千米,轿车每小时行驶60千米,客车每小时行驶50千米;
(1)轿车、客车分别从合面、上马同时相向而行,两车多少小时后相遇?
合面
上马
解:设两车X小时后相遇,依据题意得:
50X+60X=11
(50+60)X=11
解得:X=0.1
检验:X=0.1适合方程,且符合题意。
答:两车0.1小时后相遇。
客车行驶的速度:________;
列方程:________________
客车行驶的路程
客车行驶的时间:________;
客车行驶的路程:________;
轿车行驶的速度:________;
轿车行驶的时间:______;
轿车行驶的路程:________;
轿车行驶的路程
上马、合面之间的距离
50千米/时
X小时
50X千米
60千米/时
X小时
60X千米
50X+60X=11
分析:设两车X小时后相遇,则:
客车
轿车
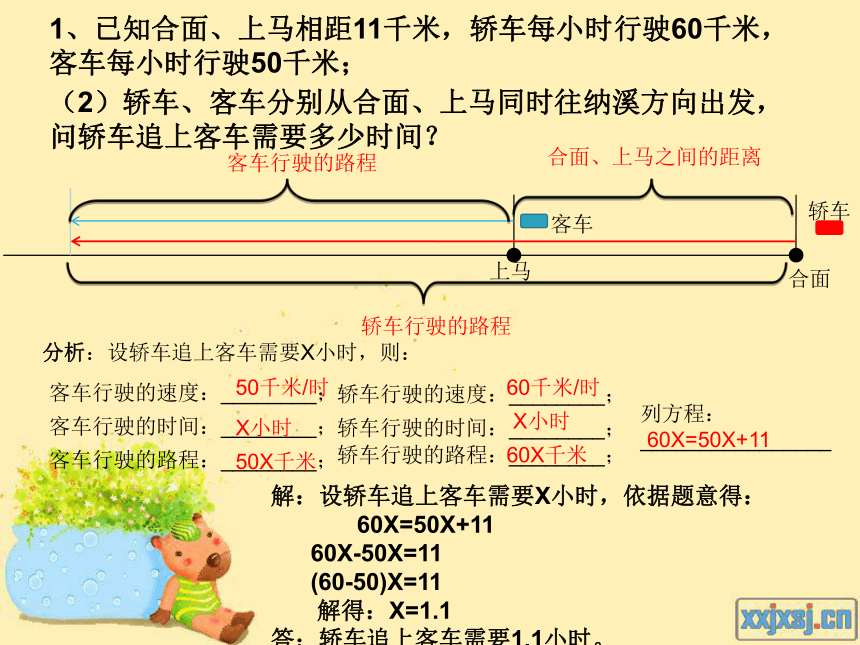
1、已知合面、上马相距11千米,轿车每小时行驶60千米,客车每小时行驶50千米;
(2)轿车、客车分别从合面、上马同时往纳溪方向出发,问轿车追上客车需要多少时间?
上马
合面
解:设轿车追上客车需要X小时,依据题意得:
60X=50X+11
60X-50X=11
(60-50)X=11
解得:X=1.1
答:轿车追上客车需要1.1小时。
客车行驶的速度:________;
列方程:________________
客车行驶的时间:________;
客车行驶的路程:________;
轿车行驶的速度:________;
轿车行驶的时间:________;
轿车行驶的路程:________;
50千米/时
X小时
50X千米
60千米/时
X小时
60X千米
60X=50X+11
分析:设轿车追上客车需要X小时,则:
合面、上马之间的距离
客车行驶的路程
轿车行驶的路程
客车
轿车
练习 甲、乙两车分别从相距240千米的A、B两地同时相向而行,已知甲车每小时比乙车多行驶10千米,两车2小时后相遇,求甲、乙两车的速度。
解:设乙车的速度为X千米/小时,则甲车的速度为(X+10)千米/小时,依据题意得:
练习 甲从A地以6千米/小时的速度向B地行驶,40分钟后,乙从A地以8千米/时的速度追甲,结果在甲离B地还有5千米的地方追上了甲,求A、B两地的距离。
题目中的等量关系是什么?
甲的路程=乙的路程
甲行驶的时间 乙行驶的时间=
速度(千米/小时) 路程(千米) 时间(小时)
甲
乙
环形问题
例 甲、乙两人环湖散步,环湖一周是400米,甲每分钟走80米,乙的每分钟走100米,
(1)甲、乙两人在同地背向而行,多长时间后两人首次
相遇?
(2)甲、乙两人在同地同向而行,多长时间后两人首次
相遇?
请你找出题中的等量关系?
(1)甲的路程 + 乙的路程=一周=400米
出发
解:设经过x分钟首次相遇,则依题意可得
100x-80x=400
解得:x=20
答:经过20分钟甲、乙相遇。
(2)乙的路程 —甲的路程=一周=400米
开始
分析:圆形路径中的规律:
快的人走的路程-慢的人走的路程=1圈(第1次相遇)
快的人走的路程-慢的人走的路程=2圈(第2次相遇)
快的人走的路程-慢的人走的路程=3圈(第3次相遇)
……….
(3)甲、乙两人在同地同向而行,多长时间后两人第2次相遇?
一元一次方程的应用
之
“行程问题”
1、已知合面、上马两地相距11千米,轿车每小时行驶60千米,客车每小时行驶50千米;
(1)轿车、客车分别从合面、上马同时相向而行,两车多少小时后相遇?
合面
上马
解:设两车X小时后相遇,依据题意得:
50X+60X=11
(50+60)X=11
解得:X=0.1
检验:X=0.1适合方程,且符合题意。
答:两车0.1小时后相遇。
客车行驶的速度:________;
列方程:________________
客车行驶的路程
客车行驶的时间:________;
客车行驶的路程:________;
轿车行驶的速度:________;
轿车行驶的时间:______;
轿车行驶的路程:________;
轿车行驶的路程
上马、合面之间的距离
50千米/时
X小时
50X千米
60千米/时
X小时
60X千米
50X+60X=11
分析:设两车X小时后相遇,则:
客车
轿车
1、已知合面、上马相距11千米,轿车每小时行驶60千米,客车每小时行驶50千米;
(2)轿车、客车分别从合面、上马同时往纳溪方向出发,问轿车追上客车需要多少时间?
上马
合面
解:设轿车追上客车需要X小时,依据题意得:
60X=50X+11
60X-50X=11
(60-50)X=11
解得:X=1.1
答:轿车追上客车需要1.1小时。
客车行驶的速度:________;
列方程:________________
客车行驶的时间:________;
客车行驶的路程:________;
轿车行驶的速度:________;
轿车行驶的时间:________;
轿车行驶的路程:________;
50千米/时
X小时
50X千米
60千米/时
X小时
60X千米
60X=50X+11
分析:设轿车追上客车需要X小时,则:
合面、上马之间的距离
客车行驶的路程
轿车行驶的路程
客车
轿车
练习 甲、乙两车分别从相距240千米的A、B两地同时相向而行,已知甲车每小时比乙车多行驶10千米,两车2小时后相遇,求甲、乙两车的速度。
解:设乙车的速度为X千米/小时,则甲车的速度为(X+10)千米/小时,依据题意得:
练习 甲从A地以6千米/小时的速度向B地行驶,40分钟后,乙从A地以8千米/时的速度追甲,结果在甲离B地还有5千米的地方追上了甲,求A、B两地的距离。
题目中的等量关系是什么?
甲的路程=乙的路程
甲行驶的时间 乙行驶的时间=
速度(千米/小时) 路程(千米) 时间(小时)
甲
乙
环形问题
例 甲、乙两人环湖散步,环湖一周是400米,甲每分钟走80米,乙的每分钟走100米,
(1)甲、乙两人在同地背向而行,多长时间后两人首次
相遇?
(2)甲、乙两人在同地同向而行,多长时间后两人首次
相遇?
请你找出题中的等量关系?
(1)甲的路程 + 乙的路程=一周=400米
出发
解:设经过x分钟首次相遇,则依题意可得
100x-80x=400
解得:x=20
答:经过20分钟甲、乙相遇。
(2)乙的路程 —甲的路程=一周=400米
开始
分析:圆形路径中的规律:
快的人走的路程-慢的人走的路程=1圈(第1次相遇)
快的人走的路程-慢的人走的路程=2圈(第2次相遇)
快的人走的路程-慢的人走的路程=3圈(第3次相遇)
……….
(3)甲、乙两人在同地同向而行,多长时间后两人第2次相遇?
