七年级数学一元一次方程解应用题(4)行程问题
文档属性
| 名称 | 七年级数学一元一次方程解应用题(4)行程问题 |

|
|
| 格式 | rar | ||
| 文件大小 | 618.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-07 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
一元一次方程解应用题(4)
——行程问题
行程问题的基本量:
路程、时间、速度
三者之间关系:
例1 某部队进行一次行军训练,规定3.5小时走完全程并返回营地,期间休息15分钟,已知从营地出发的速度为7千米/小时,返回营地的速度为6千米/小时。问部队从营地出发最远走多少千米就需返回?
题目中的等量关系是什么?
部队走出去的时间+返回的时间+休息的时间=3.5小时
基本行程问题
练习:用汽车将一批货物运往某地,去时每小时行45公里,由原路回来时,因空车每小时行50公里,结果比去时少用了1小时赶回原地,问去时和回来时各用了多少时间。
例2 甲乙两地相距450千米,两列车同时开出,相向而行,快车从甲站开出,每小时行驶85千米,慢车从乙站开出,每小时行驶65千米。多少小时后相遇?
450千米
解得:x=3
答:它们3小时可以相遇。
解:设它们x小时可以相遇,根据题意得
85x+65x=450
(85+65)x=450
85x千米
65x千米
相遇问题
甲
乙
练习:若快车先开30分钟,那么慢车行驶了多少小时后两车相遇?
相遇问题:
行的路程+乙行的路程=总路程
(甲的速度+乙的速度)×时间=总路程
一、相遇问题的基本题型
1、同时出发(两段)
二、相遇问题的等量关系
2、不同时出发 (三段 )
追及问题
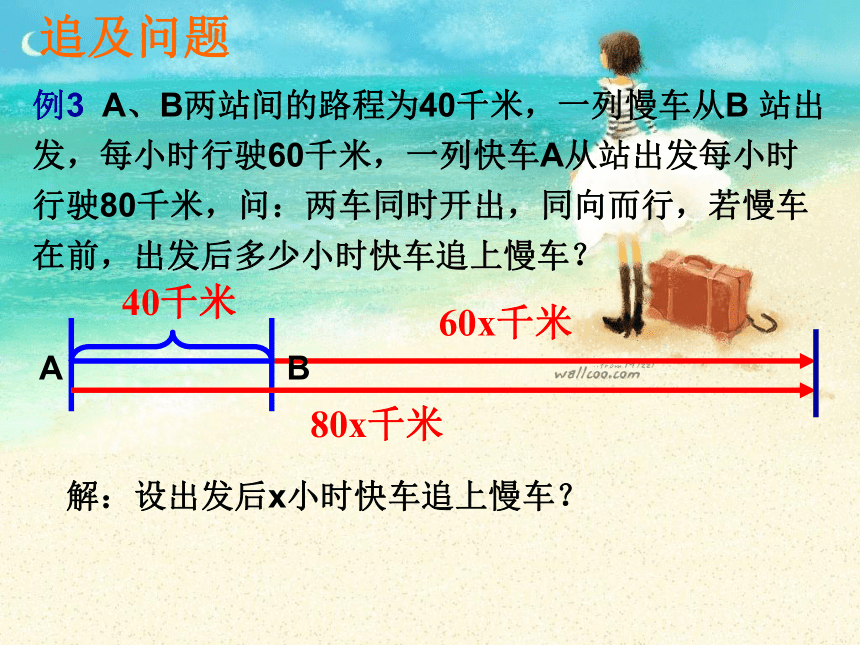
例3 A、B两站间的路程为40千米,一列慢车从B 站出发,每小时行驶60千米,一列快车A从站出发每小时行驶80千米,问:两车同时开出,同向而行,若慢车在前,出发后多少小时快车追上慢车?
40千米
A
B
解:设出发后x小时快车追上慢车?
60x千米
80x千米
练习 甲、乙两车自西向东行驶,甲车的速度是每小时48千米,乙车的速度是每小时72千米,甲车开出25分钟后乙车开出,问几小时后乙车追上甲车?
分析:
A
甲先走25分钟的路程
甲走 小时所走的路程
乙走 小时所走的路程
C
B
设x小时后乙车追上甲车
相等关系:
甲走的路程=乙走的路程
X
X
×48
48x
72x
追及问题:
追赶时快的行的路程-追赶时慢的行的路程=追及的路程
(快的速度-慢的速度)×追的时间=追及的路程
小结
(1)从时间考虑:
速度慢的用时-速度快的用时=多用的时间
(2)从路程考虑:
速度快的行程-速度慢的行程=两者的距离
行程问题中的基本等量关系为:
路程=速度×时间,
一般可从下面两个方面寻找追及问题中的等量关系:
练习 甲从A地以6千米/小时的速度向B地行驶,40分钟后,乙从A地以8千米/时的速度追甲,结果在甲离B地还有5千米的地方追上了甲,求A、B两地的距离。
题目中的等量关系是什么?
甲的路程=乙的路程
甲行驶的时间 乙行驶的时间=
速度(千米/小时) 路程(千米) 时间(小时)
甲
乙
练习:
一列货车与一列客车从相距360千米的两地同向开出,货车比客车早开出45分钟,已知货车的速度为48千米/小时,客车的速度为72千米/小时,问能否在客车开出16小时内追上货车?
环形问题
例 甲、乙两人环湖散步,环湖一周是400米,甲每分钟走80米,乙的每分钟走100米,
(1)甲、乙两人在同地背向而行,多长时间后两人首次
相遇?
(2)甲、乙两人在同地同向而行,多长时间后两人首次
相遇?
请你找出题中的等量关系
(1)甲的路程 + 乙的路程=一周=400米
(2)乙的路程 —甲的路程=一周=400米
2、 运动场的跑道一圈长400m,甲练习骑自行车,平均每分骑350m,乙练习跑步,平均每分跑250m.两人从同一处同时同向出发,经过多少时间首次相遇?
解:设经过x分钟首次相遇,则依题意可得
350x-250x=400 解得:x=4
答:经过4分钟甲、乙相遇。
分析:圆形跑道中的规律:
快的人跑的路程-慢的人跑的路程=1圈(第1次相遇)
快的人跑的路程-慢的人跑的路程=2圈(第2次相遇)
快的人跑的路程-慢的人跑的路程=3圈(第3次相遇)
……….
例5 某轮船航行于 两码头之间,从 到 顺水航行需6小时,从 到 逆水航行需10小时。已知轮船在静水中航行的速度为12千米/小时,求水流的速度和两码头 之间的距离。
顺水速度 = 静水速度 + 水流速度
逆水速度 = 静水速度 水流速度
顺水速度、逆水速度、静水速度、水流速度四者之间的关系是:
本题中的等量关系还有哪些?
轮船在顺水中航行的路程=轮船在逆水中航行的路程
顺水航行的水流速度=逆水航行的水流速度
航行问题
练习:一架飞机飞行在两个城市之间,顺风需2小时45分钟,逆风需3小时,已知风速为20千米/小时,求两个城市之间的距离。
巩固练习
1.AB两地相距480千米,一慢车从A地开出,每小时走60千米,一快车从B地开出每小时走65千米,
(1)两车同时开出,相向而行,x小时相遇,则可列方程 ;
(2)两车同时开出,背向而行,x小时后两车相距620千米,则可列方程为 ;
(3)慢车先开出1小时,相向而行,快车开出x小时相遇,则可列方程为 ;
(4)若两车同时开出,同向而行,快车在慢车后面,
x小时后快车追上慢车,则可列方程为 ;
(5)若两车同时开出,慢车在快车后面,同向而行,x小时后快车与慢车相距640千米,则可列方程为 。
2.联络员用每小时8千米的速度从甲地到乙地,回来时走比原路程长3千米的另一条路线,速度为每小时9千米,这样回来比去时多用小时,求甲、乙两地原路长。
3.甲、乙人从相距60千米的两地同时出发相向而行,甲步行速度为5千米/时,乙骑自行车,3小时后两人相遇,求乙的速度。若甲、乙两人同向而行,甲在前,乙在后,则经过多少小时乙追上甲?
4.甲、乙两人骑自行车从相距75千米的两地相向而行,甲行了2小时20分钟后乙开始动身,又经过1小时40分钟两人相遇,已知甲比乙每小时慢2.5千米,问:甲、乙两人每小时骑多少千米?
5.甲列车从A地以50千米/时的速度开往B地,一小时后,乙列车从B地以70千米/时的速度开往A地。若A、B两地相距200千米,求两车相遇点距A地多远?
6.甲、乙、丙三人,甲每分钟走60米,乙每分钟走70米,丙每分钟走80千米,若甲、乙两人从A地,丙从B地同时相向而行,丙在遇甲前10分钟遇到乙,求AB两地距离。
一.列方程解决实际问题的基本步骤:
审 设 列 解 检 答
二.相遇问题:
等量关系:
甲行驶的路程+乙行驶的路程=总路程
甲行驶的路程+乙行驶的路程+距离=总路程
乙行驶的路程=甲行驶的路程+距离
三.追及问题:
等量关系:
一元一次方程解应用题(4)
——行程问题
行程问题的基本量:
路程、时间、速度
三者之间关系:
例1 某部队进行一次行军训练,规定3.5小时走完全程并返回营地,期间休息15分钟,已知从营地出发的速度为7千米/小时,返回营地的速度为6千米/小时。问部队从营地出发最远走多少千米就需返回?
题目中的等量关系是什么?
部队走出去的时间+返回的时间+休息的时间=3.5小时
基本行程问题
练习:用汽车将一批货物运往某地,去时每小时行45公里,由原路回来时,因空车每小时行50公里,结果比去时少用了1小时赶回原地,问去时和回来时各用了多少时间。
例2 甲乙两地相距450千米,两列车同时开出,相向而行,快车从甲站开出,每小时行驶85千米,慢车从乙站开出,每小时行驶65千米。多少小时后相遇?
450千米
解得:x=3
答:它们3小时可以相遇。
解:设它们x小时可以相遇,根据题意得
85x+65x=450
(85+65)x=450
85x千米
65x千米
相遇问题
甲
乙
练习:若快车先开30分钟,那么慢车行驶了多少小时后两车相遇?
相遇问题:
行的路程+乙行的路程=总路程
(甲的速度+乙的速度)×时间=总路程
一、相遇问题的基本题型
1、同时出发(两段)
二、相遇问题的等量关系
2、不同时出发 (三段 )
追及问题
例3 A、B两站间的路程为40千米,一列慢车从B 站出发,每小时行驶60千米,一列快车A从站出发每小时行驶80千米,问:两车同时开出,同向而行,若慢车在前,出发后多少小时快车追上慢车?
40千米
A
B
解:设出发后x小时快车追上慢车?
60x千米
80x千米
练习 甲、乙两车自西向东行驶,甲车的速度是每小时48千米,乙车的速度是每小时72千米,甲车开出25分钟后乙车开出,问几小时后乙车追上甲车?
分析:
A
甲先走25分钟的路程
甲走 小时所走的路程
乙走 小时所走的路程
C
B
设x小时后乙车追上甲车
相等关系:
甲走的路程=乙走的路程
X
X
×48
48x
72x
追及问题:
追赶时快的行的路程-追赶时慢的行的路程=追及的路程
(快的速度-慢的速度)×追的时间=追及的路程
小结
(1)从时间考虑:
速度慢的用时-速度快的用时=多用的时间
(2)从路程考虑:
速度快的行程-速度慢的行程=两者的距离
行程问题中的基本等量关系为:
路程=速度×时间,
一般可从下面两个方面寻找追及问题中的等量关系:
练习 甲从A地以6千米/小时的速度向B地行驶,40分钟后,乙从A地以8千米/时的速度追甲,结果在甲离B地还有5千米的地方追上了甲,求A、B两地的距离。
题目中的等量关系是什么?
甲的路程=乙的路程
甲行驶的时间 乙行驶的时间=
速度(千米/小时) 路程(千米) 时间(小时)
甲
乙
练习:
一列货车与一列客车从相距360千米的两地同向开出,货车比客车早开出45分钟,已知货车的速度为48千米/小时,客车的速度为72千米/小时,问能否在客车开出16小时内追上货车?
环形问题
例 甲、乙两人环湖散步,环湖一周是400米,甲每分钟走80米,乙的每分钟走100米,
(1)甲、乙两人在同地背向而行,多长时间后两人首次
相遇?
(2)甲、乙两人在同地同向而行,多长时间后两人首次
相遇?
请你找出题中的等量关系
(1)甲的路程 + 乙的路程=一周=400米
(2)乙的路程 —甲的路程=一周=400米
2、 运动场的跑道一圈长400m,甲练习骑自行车,平均每分骑350m,乙练习跑步,平均每分跑250m.两人从同一处同时同向出发,经过多少时间首次相遇?
解:设经过x分钟首次相遇,则依题意可得
350x-250x=400 解得:x=4
答:经过4分钟甲、乙相遇。
分析:圆形跑道中的规律:
快的人跑的路程-慢的人跑的路程=1圈(第1次相遇)
快的人跑的路程-慢的人跑的路程=2圈(第2次相遇)
快的人跑的路程-慢的人跑的路程=3圈(第3次相遇)
……….
例5 某轮船航行于 两码头之间,从 到 顺水航行需6小时,从 到 逆水航行需10小时。已知轮船在静水中航行的速度为12千米/小时,求水流的速度和两码头 之间的距离。
顺水速度 = 静水速度 + 水流速度
逆水速度 = 静水速度 水流速度
顺水速度、逆水速度、静水速度、水流速度四者之间的关系是:
本题中的等量关系还有哪些?
轮船在顺水中航行的路程=轮船在逆水中航行的路程
顺水航行的水流速度=逆水航行的水流速度
航行问题
练习:一架飞机飞行在两个城市之间,顺风需2小时45分钟,逆风需3小时,已知风速为20千米/小时,求两个城市之间的距离。
巩固练习
1.AB两地相距480千米,一慢车从A地开出,每小时走60千米,一快车从B地开出每小时走65千米,
(1)两车同时开出,相向而行,x小时相遇,则可列方程 ;
(2)两车同时开出,背向而行,x小时后两车相距620千米,则可列方程为 ;
(3)慢车先开出1小时,相向而行,快车开出x小时相遇,则可列方程为 ;
(4)若两车同时开出,同向而行,快车在慢车后面,
x小时后快车追上慢车,则可列方程为 ;
(5)若两车同时开出,慢车在快车后面,同向而行,x小时后快车与慢车相距640千米,则可列方程为 。
2.联络员用每小时8千米的速度从甲地到乙地,回来时走比原路程长3千米的另一条路线,速度为每小时9千米,这样回来比去时多用小时,求甲、乙两地原路长。
3.甲、乙人从相距60千米的两地同时出发相向而行,甲步行速度为5千米/时,乙骑自行车,3小时后两人相遇,求乙的速度。若甲、乙两人同向而行,甲在前,乙在后,则经过多少小时乙追上甲?
4.甲、乙两人骑自行车从相距75千米的两地相向而行,甲行了2小时20分钟后乙开始动身,又经过1小时40分钟两人相遇,已知甲比乙每小时慢2.5千米,问:甲、乙两人每小时骑多少千米?
5.甲列车从A地以50千米/时的速度开往B地,一小时后,乙列车从B地以70千米/时的速度开往A地。若A、B两地相距200千米,求两车相遇点距A地多远?
6.甲、乙、丙三人,甲每分钟走60米,乙每分钟走70米,丙每分钟走80千米,若甲、乙两人从A地,丙从B地同时相向而行,丙在遇甲前10分钟遇到乙,求AB两地距离。
一.列方程解决实际问题的基本步骤:
审 设 列 解 检 答
二.相遇问题:
等量关系:
甲行驶的路程+乙行驶的路程=总路程
甲行驶的路程+乙行驶的路程+距离=总路程
乙行驶的路程=甲行驶的路程+距离
三.追及问题:
等量关系:
