16.3 二次根式的加减(1)课件(共22张PPT)
文档属性
| 名称 | 16.3 二次根式的加减(1)课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-14 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
人教版
八年级数学上
16.3二次根式的加减(1)
学习目标
1.了解二次根式的加、减运算法则.(重点)
2.会用二次根式的加、减运算法则进行简单的运算.
(难点)
回顾旧知
问题1
满足什么条件的根式是最简二次根式?
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
问题2
化简下列两组二次根式,每组化简后有什么共同特点?
化简后被开方数相同
合作探究---二次根式的加减法法则
a
a
a
a
a
a
a
a
a
a
=
+
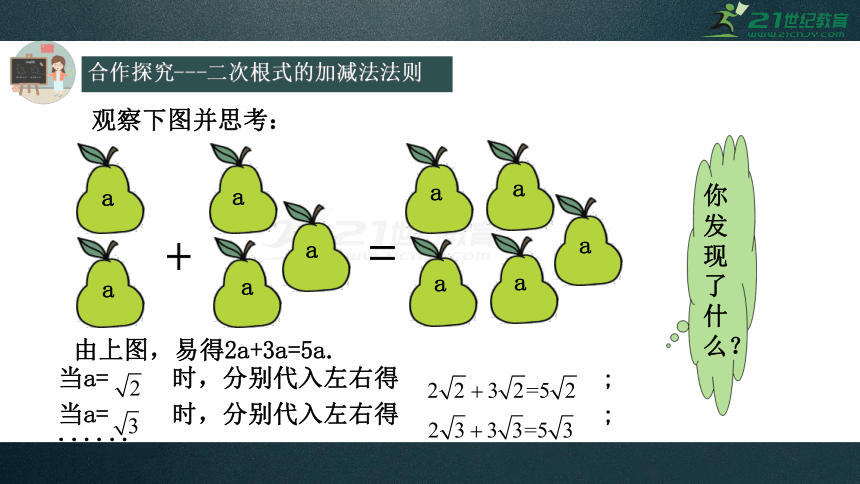
观察下图并思考:
由上图,易得2a+3a=5a.
当a=
时,分别代入左右得
;
当a=
时,分别代入左右得
;
......
你发现了什么?
合作探究---二次根式的加减法法则
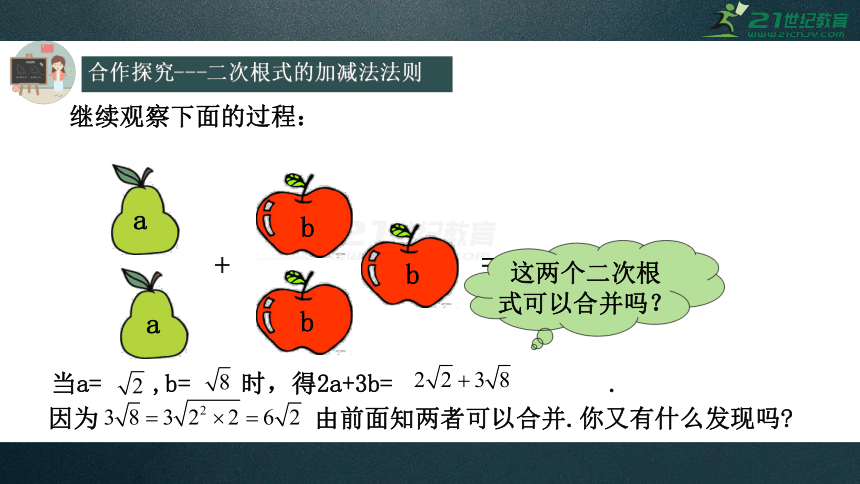
因为
由前面知两者可以合并.你又有什么发现吗?
当a=
,b=
时,得2a+3b=
.
a
2a+3b
b
=
+
b
b
a
这两个二次根式可以合并吗?
继续观察下面的过程:
合作探究---二次根式的加减法法则
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
特别强调:
1、判断几个二次根式是否可以合并,一定都要化为最简二次根式再判断.
2、被开方数相同的最简二次根式叫做同类二次根式;
3.合并的方法与合并同类项类似,利用乘法分配律,把根号外的因数(式)相加,根指数和被开方数(式)不变.如:
小试牛刀
1.下列各式中,与
是同类二次根式的是(
)
A.
B.
C.
D.
D
2.
与最简二次根式
能合并,则m=_____.
1
3.下列二次根式,不能与
合并的是________(填序号).
②⑤
学以致用
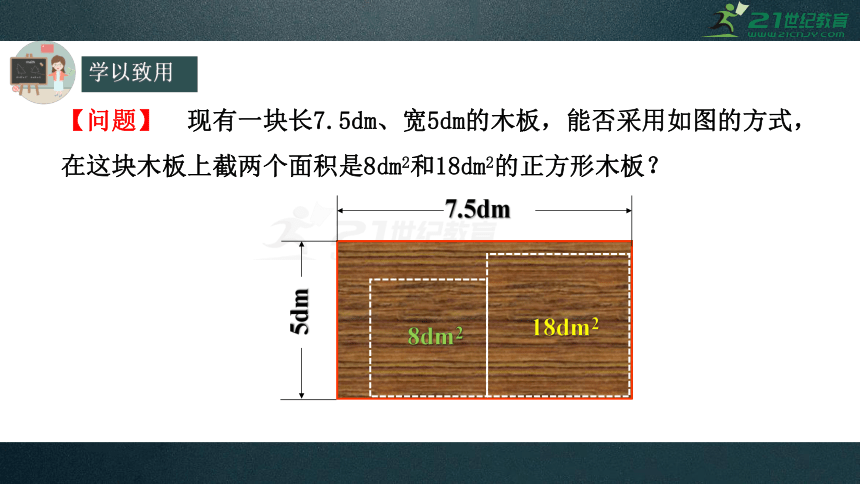
【问题】 现有一块长7.5dm、宽5dm的木板,能否采用如图的方式,在这块木板上截两个面积是8dm2和18dm2的正方形木板?
7.5dm
5dm
8dm2
18dm2
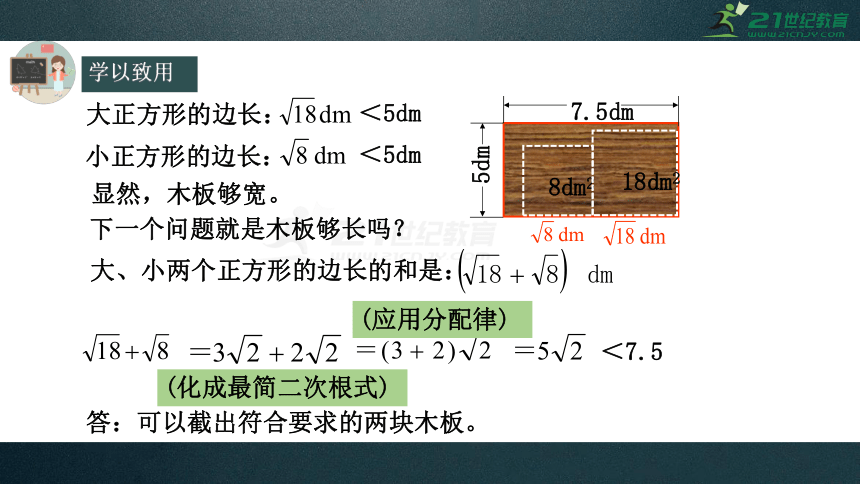
学以致用
大正方形的边长:
小正方形的边长:
<5dm
<5dm
显然,木板够宽。
7.5dm
5dm
8dm2
18dm2
下一个问题就是木板够长吗?
大、小两个正方形的边长的和是:
(化成最简二次根式)
(应用分配律)
<7.5
答:可以截出符合要求的两块木板。
典例精析
例1、计算
⑴
⑵
解:⑴原式=
⑵
原式=
典例精析
例2
计算:
解:
有括号,先去括号
归纳:加减法的运算步骤:(1)化——将非最简二次根式的二次根式化简;
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
“一化简二判断三合并”
小试牛刀
解:原式=
(1)
原式=
(2)
小试牛刀
原式=
(4)
(3)
原式=
综合演练
1.二次根式:
中,与
能进行合并的是(
)
A.
B
.
C
.
D
.
2.下列运算中错误的是
(
)
A.
B.
C.
D.
A
C
综合演练
3.三角形的三边长分别为
则这个三角形的周长为__________.
4.计算:
综合演练
5.若最简根式
与
可以合并,求
的值.
解:由题意得
解得
即
知识点拨:确定可以合并的二次根式中字母取值的方法:利用被开方数相同,指数都为2,列关于待定字母的方程求解即可.
综合演练
6、有一个等腰三角形的两边长分别为
,求其周长.
解:?当腰长为
时,
∵
∴此时能构成三角形,周长为
?
当腰长为
时,
∵
∴此时能构成三角形,周长为
知识点拨:二次根式的加减与等腰三角形的综合运用,关键是要分类讨论及会比较两个二次根式的大小.
综合演练
7.如图,两个圆的圆心相同.已知大圆和小圆的面积分别为25.12和12.56,求圆环的宽度d(π取3.14,结果保留小数点后两位).
d
解
设大圆和小圆的半径分别为R,r,面积分别为
,
,
由
,
可知
则
综合演练
解
设大圆和小圆的半径分别为R,r,面积分别为
,
,由
,
可知
则
答:圆环的宽度为
d
课堂小结
本节课你有哪些收获?
如何进行二次根式的加减运算?
课后作业
教材10页习题16.3第2、3题.
https://www.21cnjy.com/help/help_extract.php
人教版
八年级数学上
16.3二次根式的加减(1)
学习目标
1.了解二次根式的加、减运算法则.(重点)
2.会用二次根式的加、减运算法则进行简单的运算.
(难点)
回顾旧知
问题1
满足什么条件的根式是最简二次根式?
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
问题2
化简下列两组二次根式,每组化简后有什么共同特点?
化简后被开方数相同
合作探究---二次根式的加减法法则
a
a
a
a
a
a
a
a
a
a
=
+
观察下图并思考:
由上图,易得2a+3a=5a.
当a=
时,分别代入左右得
;
当a=
时,分别代入左右得
;
......
你发现了什么?
合作探究---二次根式的加减法法则
因为
由前面知两者可以合并.你又有什么发现吗?
当a=
,b=
时,得2a+3b=
.
a
2a+3b
b
=
+
b
b
a
这两个二次根式可以合并吗?
继续观察下面的过程:
合作探究---二次根式的加减法法则
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
特别强调:
1、判断几个二次根式是否可以合并,一定都要化为最简二次根式再判断.
2、被开方数相同的最简二次根式叫做同类二次根式;
3.合并的方法与合并同类项类似,利用乘法分配律,把根号外的因数(式)相加,根指数和被开方数(式)不变.如:
小试牛刀
1.下列各式中,与
是同类二次根式的是(
)
A.
B.
C.
D.
D
2.
与最简二次根式
能合并,则m=_____.
1
3.下列二次根式,不能与
合并的是________(填序号).
②⑤
学以致用
【问题】 现有一块长7.5dm、宽5dm的木板,能否采用如图的方式,在这块木板上截两个面积是8dm2和18dm2的正方形木板?
7.5dm
5dm
8dm2
18dm2
学以致用
大正方形的边长:
小正方形的边长:
<5dm
<5dm
显然,木板够宽。
7.5dm
5dm
8dm2
18dm2
下一个问题就是木板够长吗?
大、小两个正方形的边长的和是:
(化成最简二次根式)
(应用分配律)
<7.5
答:可以截出符合要求的两块木板。
典例精析
例1、计算
⑴
⑵
解:⑴原式=
⑵
原式=
典例精析
例2
计算:
解:
有括号,先去括号
归纳:加减法的运算步骤:(1)化——将非最简二次根式的二次根式化简;
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
“一化简二判断三合并”
小试牛刀
解:原式=
(1)
原式=
(2)
小试牛刀
原式=
(4)
(3)
原式=
综合演练
1.二次根式:
中,与
能进行合并的是(
)
A.
B
.
C
.
D
.
2.下列运算中错误的是
(
)
A.
B.
C.
D.
A
C
综合演练
3.三角形的三边长分别为
则这个三角形的周长为__________.
4.计算:
综合演练
5.若最简根式
与
可以合并,求
的值.
解:由题意得
解得
即
知识点拨:确定可以合并的二次根式中字母取值的方法:利用被开方数相同,指数都为2,列关于待定字母的方程求解即可.
综合演练
6、有一个等腰三角形的两边长分别为
,求其周长.
解:?当腰长为
时,
∵
∴此时能构成三角形,周长为
?
当腰长为
时,
∵
∴此时能构成三角形,周长为
知识点拨:二次根式的加减与等腰三角形的综合运用,关键是要分类讨论及会比较两个二次根式的大小.
综合演练
7.如图,两个圆的圆心相同.已知大圆和小圆的面积分别为25.12和12.56,求圆环的宽度d(π取3.14,结果保留小数点后两位).
d
解
设大圆和小圆的半径分别为R,r,面积分别为
,
,
由
,
可知
则
综合演练
解
设大圆和小圆的半径分别为R,r,面积分别为
,
,由
,
可知
则
答:圆环的宽度为
d
课堂小结
本节课你有哪些收获?
如何进行二次根式的加减运算?
课后作业
教材10页习题16.3第2、3题.
https://www.21cnjy.com/help/help_extract.php
