五年级下册数学教案 4.5 组合体的体积 沪教版 (3)
文档属性
| 名称 | 五年级下册数学教案 4.5 组合体的体积 沪教版 (3) |

|
|
| 格式 | zip | ||
| 文件大小 | 135.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-28 00:00:00 | ||
图片预览

文档简介
教学内容:组合体的体积
教学目标
知识与技能:
A.
初步学会用割补的方法求组合体的体积
B.
根据组合图形面积计算方法,推导出组合体的体积计算方法。
C.
自主探究组合体的体积计算方法,并且会用多种方法计算。
过程与方法:
A.根据形状和尺寸,能选择合适的方法巧算组合体的体积
B.能根据形状和尺寸,熟练选择合适的方法巧算组合体的体积
C.会根据形状和尺寸,灵活选择合适的方法巧算组合体的体积
情感态度与价值观
A.
通过实际的操作过程,建立空间概念。
B.
通过自主探究,理解知识间的联系,解决新问题。
C.
自主探究会用多种方法解题。
教学重难点:
会根据不同的方法,找准各部分的尺寸
1、
新课导入
1.
长方体和正方体体积的计算公式是什么?
长方体的体积=长×宽×高
V=abh
师:除了这种方法,我们还可以怎么求长方体体积。
长方体体积=底面积×高
V=Sh
正方体的体积=棱长×棱长×棱长
V=a3
2.
求体积。
解:V=abh
解:V=a3
=8×5×10
=5×5×5
=400
(立方厘米)
=125(立方厘米)
如果把它们合在一起,会形成一个什么图形?这是组合体,这节课让我们学习组合体的体积。
3.
揭示课题:组合体的体积
2、
新课探索:
1.
请大家回忆一下,我们在计算组合图形面积的时候,首先要把不规则的图形进行割补,使它成为我们学过的基本图形,比如正方形、长方形、三角形、等等。方法有几种呢?
2.
合理割补方法:(上+下、左+右、大-小)
3、怎么才能做到合理割补呢?
(割后可以找到能计算的数据)
4、最后把每一部分结果相加减。
今天我们就用这些学过的本领来计算组合体的体积。
(1)
探究一
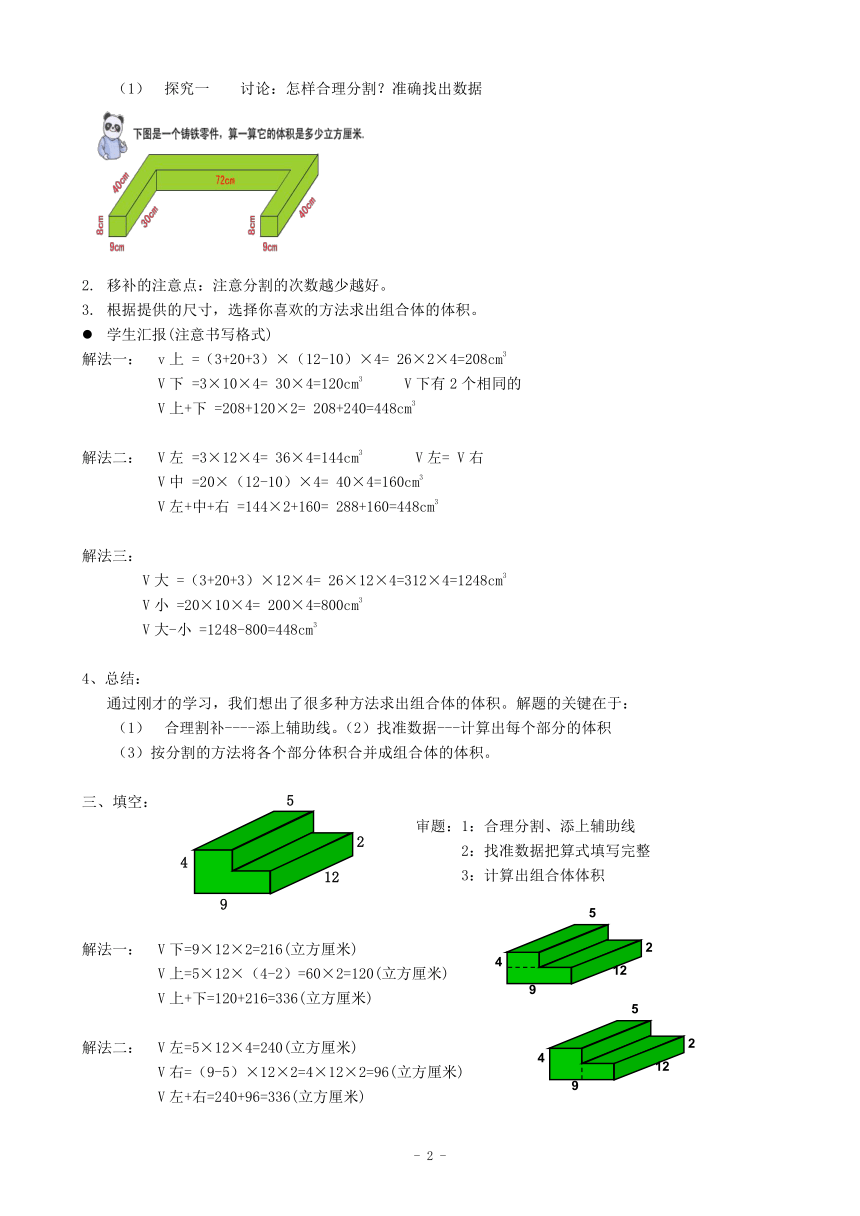
讨论:怎样合理分割?准确找出数据
1.
移补的注意点:注意分割的次数越少越好。
2.
根据提供的尺寸,选择你喜欢的方法求出组合体的体积。
?
学生汇报(注意书写格式)
解法一:
v上
=(3+20+3)×(12-10)×4=
26×2×4=208cm3
V下
=3×10×4=
30×4=120cm3
V下有2个相同的
V上+下
=208+120×2=
208+240=448cm3
解法二:
V左
=3×12×4=
36×4=144cm3
V左=
V右
V中
=20×(12-10)×4=
40×4=160cm3
V左+中+右
=144×2+160=
288+160=448cm3
解法三:
V大
=(3+20+3)×12×4=
26×12×4=312×4=1248cm3
V小
=20×10×4=
200×4=800cm3
V大-小
=1248-800=448cm3
4、总结:
通过刚才的学习,我们想出了很多种方法求出组合体的体积。解题的关键在于:
(1)
合理割补----添上辅助线。(2)找准数据---计算出每个部分的体积
(3)按分割的方法将各个部分体积合并成组合体的体积。
三、填空:
审题:1:合理分割、添上辅助线
2:找准数据把算式填写完整
3:计算出组合体体积
解法一:
V下=9×12×2=216(立方厘米)
V上=5×12×(4-2)=60×2=120(立方厘米)
V上+下=120+216=336(立方厘米)
解法二:
V左=5×12×4=240(立方厘米)
V右=(9-5)×12×2=4×12×2=96(立方厘米)
V左+右=240+96=336(立方厘米)
解法三:
V大=9×12×4=432(立方厘米)
V小=(9-5)×12×(4-2)=4×12×2=96(立方厘米)
V大-小=432-96=336(立方厘米)
四、
巧算组合体的体积
刚才我们用了那么多种方法求组合体的体积,有些方法用的巧,能帮助我们快速地求出组合体的体积。
判断下列算法是否正确?还有没有其他想法?
1
解:V=(1×1×6)×1
⑵
解:V=(4×3×1)÷2
=6(dm3)
(
)
=6(dm3)
(
)
3、
本课小结
今天我们学了很多种方法求组合体的体积,有哪些?你喜欢哪种方法,为什么?
班级(
)姓名(
)
根据要求填空:
1、按所给的计算步骤合理分割并添上辅助线
2、找准数据把算式填写完整并计算出组合体的体积
解法一:
V上
=5×(
)×(4-2)
=
(立方厘米)
V(
)=9×12×2=216(立方厘米)
V(
)=216+(
)=
(立方厘米)
解法二:
V左=5×(
)×4=
(立方厘米)
V右=(
)×12×2=
(立方厘米)
V左+右=(
)+(
)=
(立方厘米)
解法三:
V大=9×12×(
)=
(立方厘米)
V小=(
)×12×(
)=
(立方厘米)
V大-小=(
)-(
)=
(立方厘米)
8
10
5
5
5
5
2
12
5
4
9
2
12
5
4
9
2
12
5
4
9
2
12
5
4
9
3
3
1
1
1
1
1
2
12
5
4
9
2
12
5
4
9
2
12
5
4
9
2
12
5
4
9
PAGE
-
5
-
教学目标
知识与技能:
A.
初步学会用割补的方法求组合体的体积
B.
根据组合图形面积计算方法,推导出组合体的体积计算方法。
C.
自主探究组合体的体积计算方法,并且会用多种方法计算。
过程与方法:
A.根据形状和尺寸,能选择合适的方法巧算组合体的体积
B.能根据形状和尺寸,熟练选择合适的方法巧算组合体的体积
C.会根据形状和尺寸,灵活选择合适的方法巧算组合体的体积
情感态度与价值观
A.
通过实际的操作过程,建立空间概念。
B.
通过自主探究,理解知识间的联系,解决新问题。
C.
自主探究会用多种方法解题。
教学重难点:
会根据不同的方法,找准各部分的尺寸
1、
新课导入
1.
长方体和正方体体积的计算公式是什么?
长方体的体积=长×宽×高
V=abh
师:除了这种方法,我们还可以怎么求长方体体积。
长方体体积=底面积×高
V=Sh
正方体的体积=棱长×棱长×棱长
V=a3
2.
求体积。
解:V=abh
解:V=a3
=8×5×10
=5×5×5
=400
(立方厘米)
=125(立方厘米)
如果把它们合在一起,会形成一个什么图形?这是组合体,这节课让我们学习组合体的体积。
3.
揭示课题:组合体的体积
2、
新课探索:
1.
请大家回忆一下,我们在计算组合图形面积的时候,首先要把不规则的图形进行割补,使它成为我们学过的基本图形,比如正方形、长方形、三角形、等等。方法有几种呢?
2.
合理割补方法:(上+下、左+右、大-小)
3、怎么才能做到合理割补呢?
(割后可以找到能计算的数据)
4、最后把每一部分结果相加减。
今天我们就用这些学过的本领来计算组合体的体积。
(1)
探究一
讨论:怎样合理分割?准确找出数据
1.
移补的注意点:注意分割的次数越少越好。
2.
根据提供的尺寸,选择你喜欢的方法求出组合体的体积。
?
学生汇报(注意书写格式)
解法一:
v上
=(3+20+3)×(12-10)×4=
26×2×4=208cm3
V下
=3×10×4=
30×4=120cm3
V下有2个相同的
V上+下
=208+120×2=
208+240=448cm3
解法二:
V左
=3×12×4=
36×4=144cm3
V左=
V右
V中
=20×(12-10)×4=
40×4=160cm3
V左+中+右
=144×2+160=
288+160=448cm3
解法三:
V大
=(3+20+3)×12×4=
26×12×4=312×4=1248cm3
V小
=20×10×4=
200×4=800cm3
V大-小
=1248-800=448cm3
4、总结:
通过刚才的学习,我们想出了很多种方法求出组合体的体积。解题的关键在于:
(1)
合理割补----添上辅助线。(2)找准数据---计算出每个部分的体积
(3)按分割的方法将各个部分体积合并成组合体的体积。
三、填空:
审题:1:合理分割、添上辅助线
2:找准数据把算式填写完整
3:计算出组合体体积
解法一:
V下=9×12×2=216(立方厘米)
V上=5×12×(4-2)=60×2=120(立方厘米)
V上+下=120+216=336(立方厘米)
解法二:
V左=5×12×4=240(立方厘米)
V右=(9-5)×12×2=4×12×2=96(立方厘米)
V左+右=240+96=336(立方厘米)
解法三:
V大=9×12×4=432(立方厘米)
V小=(9-5)×12×(4-2)=4×12×2=96(立方厘米)
V大-小=432-96=336(立方厘米)
四、
巧算组合体的体积
刚才我们用了那么多种方法求组合体的体积,有些方法用的巧,能帮助我们快速地求出组合体的体积。
判断下列算法是否正确?还有没有其他想法?
1
解:V=(1×1×6)×1
⑵
解:V=(4×3×1)÷2
=6(dm3)
(
)
=6(dm3)
(
)
3、
本课小结
今天我们学了很多种方法求组合体的体积,有哪些?你喜欢哪种方法,为什么?
班级(
)姓名(
)
根据要求填空:
1、按所给的计算步骤合理分割并添上辅助线
2、找准数据把算式填写完整并计算出组合体的体积
解法一:
V上
=5×(
)×(4-2)
=
(立方厘米)
V(
)=9×12×2=216(立方厘米)
V(
)=216+(
)=
(立方厘米)
解法二:
V左=5×(
)×4=
(立方厘米)
V右=(
)×12×2=
(立方厘米)
V左+右=(
)+(
)=
(立方厘米)
解法三:
V大=9×12×(
)=
(立方厘米)
V小=(
)×12×(
)=
(立方厘米)
V大-小=(
)-(
)=
(立方厘米)
8
10
5
5
5
5
2
12
5
4
9
2
12
5
4
9
2
12
5
4
9
2
12
5
4
9
3
3
1
1
1
1
1
2
12
5
4
9
2
12
5
4
9
2
12
5
4
9
2
12
5
4
9
PAGE
-
5
-
