三角形全等判定(3)课件1
文档属性
| 名称 | 三角形全等判定(3)课件1 |

|
|
| 格式 | rar | ||
| 文件大小 | 394.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-07 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
知识回顾
前几节我们探究了两个
三角形满足什么条件时,这两个三角形全等?你认为还有其他情况吗?
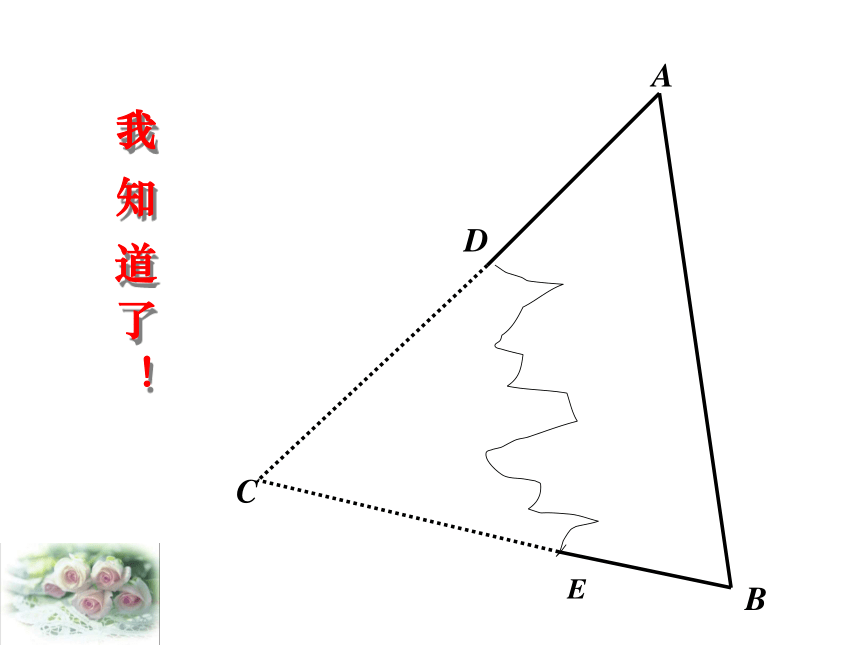
一张教学用的三角形硬纸板不小心
被撕坏了,如图,你能制作一张与原来
同样大小的新教具?能恢复原来三角形
的原貌吗?
怎么办?可以帮帮我吗?
C
B
E
A
D
我 知 道了!
先任意画出一个△ABC,再画一个△A/B/C/,使A/B/=AB,∠A/ =∠A, ∠B/ =∠B .把画好的△A/B/C/剪下,放到△ABC上,它们全等吗?
我探究,我发现!
B
A
C
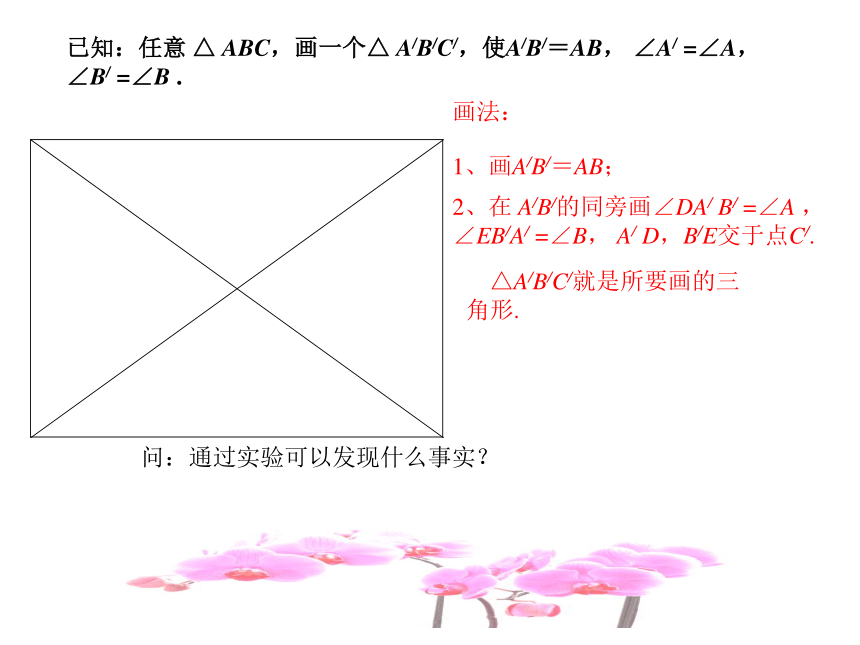
已知:任意 △ ABC,画一个△ A/B/C/,使A/B/=AB, ∠A/ =∠A, ∠B/ =∠B .
画法:
2、在 A/B/的同旁画∠DA/ B/ =∠A , ∠EB/A/ =∠B, A/ D,B/E交于点C/.
1、画A/B/=AB;
△A/B/C/就是所要画的三角形.
问:通过实验可以发现什么事实?
有两角和它们夹边
对应相等的两个三角形
全等(简写成“角边角”或“ASA”).
探究反映的规律是:
1.已知:如图,AB=A‘C,∠A=∠A ’ ,
∠B=∠C 求证:△ABE≌ △A ' CD
练习1
∠A=∠A’ (已知 )
AB=A’C(已知 )
∠B=∠C(已知 )
证明:在△ABE和△A’CD中
∴ △ABE≌△A’CD(ASA)
在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF,如图, △ABC与△DEF全等吗?能利用角边角证明你的结论吗?
探究6
A
B
C
D
E
F
有两角和其中一角
的对边对应相等的两个
三角形全等(简写成“角
角边”或“AAS”).
探究反映的规律是:
例题讲解:
例3.已知:点D在AB上,点E在AC上,BE和CD相交于
点O,AB=AC,∠B=∠C.
求证:BD=CE
证明 :在△ADC和△AEB中
∠A=∠A(公共角)
AC=AB(已知)
∠C=∠B(已知)
∴△ACD≌△ABE(ASA)
∴AD=AE(全等三角形的对应边相等)
又∵AB=AC(已知)
∴BD=CE
2.如图,∠1=∠2,∠3=∠4
求证:AC=AD
证明:∵∠ABD=180°-∠3
∠ABC=180°-∠4
而∠3=∠4(已知)
∴∠ABD=∠ABC
在△ABD和△ABC中
∠1=∠2(已知 )
AB=AB (公共边)
∠ABD=∠ABC (已知 )
∴△ABD ≌ △ABC(ASA )
∴AC=AD (全等三角形对应边相等)
1
2
3
4
练习2
3、已知,如图,∠1=∠2,∠C=∠D
求证:AC=AD
在△ABD和△ABC中
∠1=∠2 (已知)
∠C=∠D(已知)
AB=AB(公共边)
∴△ABD≌△ABC (AAS)
∴AC=AD (全等三角形对应边相等)
证明:
1
2
变式
4.如图,应填什么就有 △AOC≌ △BOD
∠A=∠B(已知)
______
∠1=∠2 (已知)
∴△AOC≌△BOD
1
2
AO=BO或者CO=DO或者AC=BD
5、如图,已知∠1=∠2,∠3=∠4,BD=CE
求证:AB=AC
证明 :∵∠3=∠4
∴∠ 5=∠6(等角的补角相等)
在△_____和△_____中
______________( )
______________( )
______________( )
∴△ _____ ≌ △_______( )
∴AB=AC ( )
4
2
1
3
6
5
ABD
BD=CE
已知
∠1=∠2
已知
∠ 5=∠6
已证
SSA
全等三角形对应边相等
ACE
ABD
ACE
三角对应相等的两个三角形全等吗?
探究7
请你解答上述问题后把三角形全
等的方法做一个小结。
总结:
你有收获吗
还有什么疑问吗
(1)本节课学习了ASA和AAS判定三角形全等的方法,前面我们还学习了SSS、SAS
(2)要根据题意选择适当的方法.
(3)证明线段或角相等,就是证明它们所在的两个三角形全等.
必做题: 教科书P15页第5、6题
选做题: 教科书P17页第12、13题。
在数学天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
知识回顾
前几节我们探究了两个
三角形满足什么条件时,这两个三角形全等?你认为还有其他情况吗?
一张教学用的三角形硬纸板不小心
被撕坏了,如图,你能制作一张与原来
同样大小的新教具?能恢复原来三角形
的原貌吗?
怎么办?可以帮帮我吗?
C
B
E
A
D
我 知 道了!
先任意画出一个△ABC,再画一个△A/B/C/,使A/B/=AB,∠A/ =∠A, ∠B/ =∠B .把画好的△A/B/C/剪下,放到△ABC上,它们全等吗?
我探究,我发现!
B
A
C
已知:任意 △ ABC,画一个△ A/B/C/,使A/B/=AB, ∠A/ =∠A, ∠B/ =∠B .
画法:
2、在 A/B/的同旁画∠DA/ B/ =∠A , ∠EB/A/ =∠B, A/ D,B/E交于点C/.
1、画A/B/=AB;
△A/B/C/就是所要画的三角形.
问:通过实验可以发现什么事实?
有两角和它们夹边
对应相等的两个三角形
全等(简写成“角边角”或“ASA”).
探究反映的规律是:
1.已知:如图,AB=A‘C,∠A=∠A ’ ,
∠B=∠C 求证:△ABE≌ △A ' CD
练习1
∠A=∠A’ (已知 )
AB=A’C(已知 )
∠B=∠C(已知 )
证明:在△ABE和△A’CD中
∴ △ABE≌△A’CD(ASA)
在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF,如图, △ABC与△DEF全等吗?能利用角边角证明你的结论吗?
探究6
A
B
C
D
E
F
有两角和其中一角
的对边对应相等的两个
三角形全等(简写成“角
角边”或“AAS”).
探究反映的规律是:
例题讲解:
例3.已知:点D在AB上,点E在AC上,BE和CD相交于
点O,AB=AC,∠B=∠C.
求证:BD=CE
证明 :在△ADC和△AEB中
∠A=∠A(公共角)
AC=AB(已知)
∠C=∠B(已知)
∴△ACD≌△ABE(ASA)
∴AD=AE(全等三角形的对应边相等)
又∵AB=AC(已知)
∴BD=CE
2.如图,∠1=∠2,∠3=∠4
求证:AC=AD
证明:∵∠ABD=180°-∠3
∠ABC=180°-∠4
而∠3=∠4(已知)
∴∠ABD=∠ABC
在△ABD和△ABC中
∠1=∠2(已知 )
AB=AB (公共边)
∠ABD=∠ABC (已知 )
∴△ABD ≌ △ABC(ASA )
∴AC=AD (全等三角形对应边相等)
1
2
3
4
练习2
3、已知,如图,∠1=∠2,∠C=∠D
求证:AC=AD
在△ABD和△ABC中
∠1=∠2 (已知)
∠C=∠D(已知)
AB=AB(公共边)
∴△ABD≌△ABC (AAS)
∴AC=AD (全等三角形对应边相等)
证明:
1
2
变式
4.如图,应填什么就有 △AOC≌ △BOD
∠A=∠B(已知)
______
∠1=∠2 (已知)
∴△AOC≌△BOD
1
2
AO=BO或者CO=DO或者AC=BD
5、如图,已知∠1=∠2,∠3=∠4,BD=CE
求证:AB=AC
证明 :∵∠3=∠4
∴∠ 5=∠6(等角的补角相等)
在△_____和△_____中
______________( )
______________( )
______________( )
∴△ _____ ≌ △_______( )
∴AB=AC ( )
4
2
1
3
6
5
ABD
BD=CE
已知
∠1=∠2
已知
∠ 5=∠6
已证
SSA
全等三角形对应边相等
ACE
ABD
ACE
三角对应相等的两个三角形全等吗?
探究7
请你解答上述问题后把三角形全
等的方法做一个小结。
总结:
你有收获吗
还有什么疑问吗
(1)本节课学习了ASA和AAS判定三角形全等的方法,前面我们还学习了SSS、SAS
(2)要根据题意选择适当的方法.
(3)证明线段或角相等,就是证明它们所在的两个三角形全等.
必做题: 教科书P15页第5、6题
选做题: 教科书P17页第12、13题。
在数学天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
