人教版数学七年级下册 第5章 5.3平行线的性质同步测试试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学七年级下册 第5章 5.3平行线的性质同步测试试题(一)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 158.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 21:24:18 | ||
图片预览




文档简介
平行线的性质同步测试试题(一)
一.选择题
1.能说明命题“若x2≥4,则x≥2”为假命题的一个反例可以是( )
A.x=﹣1 B.x=2 C.x=﹣3 D.x=5
2.如果两个角的两边分别平行,而其中一个角比另一个角的3倍少20°,那么这两个角是( )
A.50°、130° B.都是10°
C.50°、130°或10°、10° D.以上都不对
3.下列命题错误的是( )
A.长度为 5,2,3 的三条线段可以组成三角形
B.任意三角形的内角和都是 180°
C.多边形的外角和是 360°
D.两直线平行,同位角相等
4.如图,已知AB∥CD,∠A=60°,∠ECD=120°,∠ECA的度数是( )
A.90° B.120° C.135° D.150°
5.如图,已知AB∥CD,HI∥FG,EF⊥CD于F,∠1=40°,那么∠EHI=( )
A.60° B.50° C.45° D.40°
6.下列命题正确的是( )
A.有两边和一角分别相等的两个三角形全等
B.一个多边形的内角和是它的外角和的2倍,则这个多边形是七边形
C.一组对边平行且一组对角相等的四边形是平行四边形
D.相等的圆心角所对的弧也相等
7.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③AB∥CE且∠ADC=∠B;④AB∥CE且∠BCD=∠BAD;其中能推出BC∥AD的条件为( )
A.①② B.②④ C.②③ D.②③④
8.下列命题:
①负数没有立方根;
②一个实数的算术平方根一定是正数;
③一个正数或负数的立方根与这个数同号;
④如果一个数的算术平方根是这个数本身,那么这个数是1或0;
⑤如果一个数的立方根是这个数本身,那么这个数是1或0,其中错误的有( )
A.2个 B.3个 C.4个 D.5个
9.如图,AB∥CD,AE∥CF,∠A=50°,则∠C=( )
A.40° B.50° C.60° D.70°
10.a,b,c是同一平面内的三条直线,下列说法错误的是( )
A.如果a∥b,b∥c,那么a∥c B.如果a∥b,b⊥c,那么a⊥c
C.如果a⊥c,b⊥c,那么a⊥b D.如果a⊥b,b⊥c,那么a∥c
二.填空题
11.在同一平面内,设a、b、c是三条互相平行的直线,a与b之间的距离为5,b与c之间的距离为2,则a与c之间的距离为 .
12.如图,已知∠1=110°,如果CD∥BE,那么∠B的度数为 .
13.如图,将一个长方形纸片ABCD沿EF折叠,点C恰好落在AD边上点G处,点D落在点H处.若∠CFE=72°,则∠EGH的度数为 .
14.已知,如图,点D,E分别在AB和AC上,且DE∥BC,∠A=40°,∠C=80°,则∠ADE= 度.
15.已知直线a∥b,将一块含30°角的直角三角板ABC按如图所示方式放置(∠BAC=30°),并且顶点A,C分别落在直线a,b上,若∠1=22°,则∠2的度数是 .
三.解答题
16.如图,已知BE∥FG,∠1=∠2,∠ABC=40°,试求∠ADE的度数.
17.如图,AB∥CD,点E在AC上,∠1=∠B,BE⊥DE,试说明∠2=∠D.
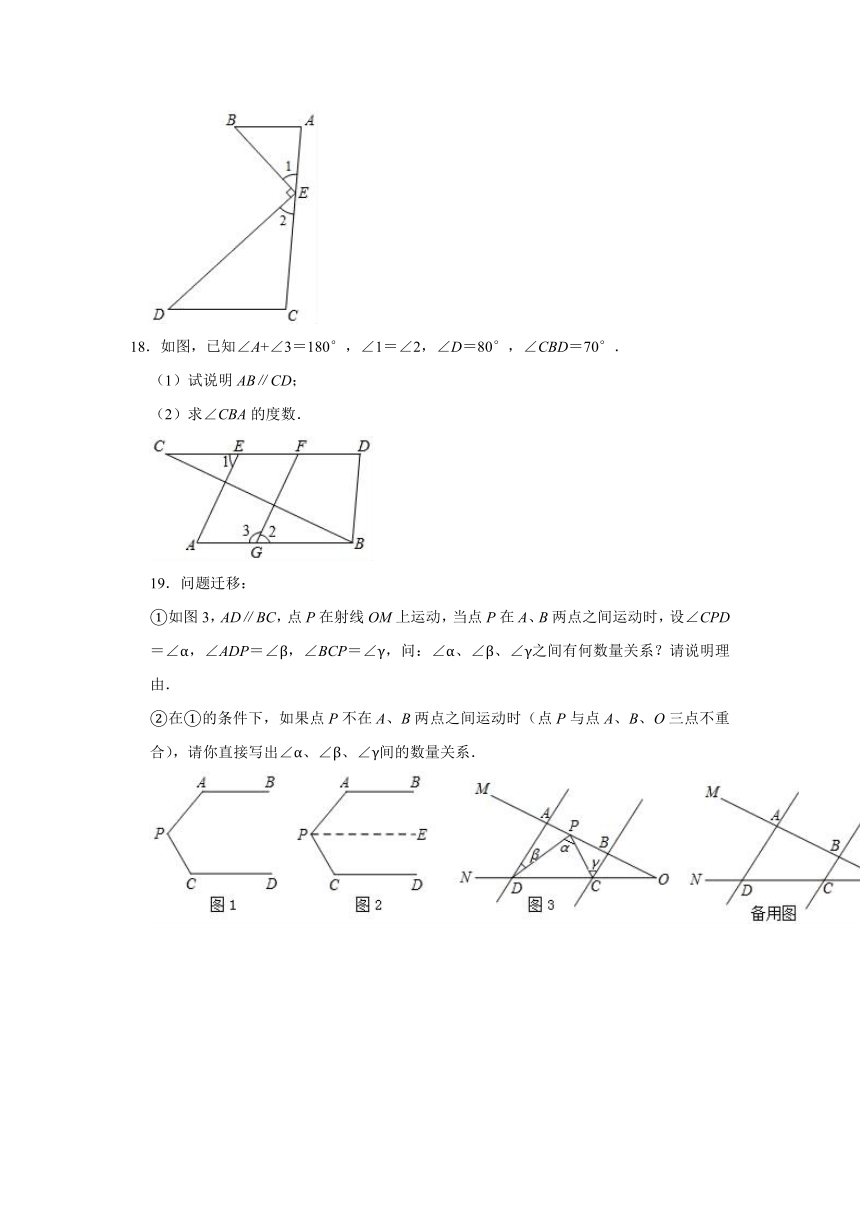
18.如图,已知∠A+∠3=180°,∠1=∠2,∠D=80°,∠CBD=70°.
(1)试说明AB∥CD;
(2)求∠CBA的度数.
19.问题迁移:
①如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,设∠CPD=∠α,∠ADP=∠β,∠BCP=∠γ,问:∠α、∠β、∠γ之间有何数量关系?请说明理由.
②在①的条件下,如果点P不在A、B两点之间运动时(点P与点A、B、O三点不重合),请你直接写出∠α、∠β、∠γ间的数量关系.
参考答案与试题解析
一.选择题
1.【解答】解:说明命题“若x2≥4,则x≥2”是假命题的一个反例可以是x=﹣3.
故选:C.
2.【解答】解:∵两个角的两边分别平行,
∴这两个角相等或互补.
设其中一角为x°,
若这两个角相等,则x=3x﹣20,
解得:x=10,
∴这两个角的度数是10°和10°;
若这两个角互补,
则180﹣x=3x﹣20,
解得:x=50,
∴这两个角的度数是50°和130°.
∴这两个角的度数是50°、130°或10°、10°.
故选:C.
3.【解答】解:A、因为2+3=5,所以长度为 5,2,3 的三条线段不可以组成三角形,原命题是错误,符合题意;
B、任意三角形的内角和都是 180°,原命题是正确,不符合题意;
C、多边形的外角和是 360°,原命题是正确,不符合题意;
D、两直线平行,同位角相等,原命题是正确,不符合题意;
故选:A.
4.【解答】解:∵AB∥CD,∠A=60°,
∴∠A+∠ACD=180°,
∴∠ACD=120°,
∵∠ECD=120°,
∴∠ECA=360°﹣∠ECD﹣∠ACD=360°﹣120°﹣120°=120°,
故选:B.
5.【解答】解:∵AB∥CD,∠1=40°,
∴∠GFD=∠1=40°,
∵EF⊥CD,
∴∠EFD=90°,
∴∠EFG=∠EFD﹣∠GFD=90°﹣40°=50°,
又∵HI∥FG,
∴∠EHI=∠EFG=50°,
故选:B.
6.【解答】解:A、有两边和其夹角分别相等的两个三角形全等,原命题是假命题;
B、一个多边形的内角和是它的外角和的2倍,则这个多边形是六边形,原命题是假命题;
C、一组对边平行且相等的四边形是平行四边形,原命题是假命题;
D、相等的圆心角所对的弧也相等,是真命题;
故选:D.
7.【解答】解:①∵∠1=∠2,
∴AB∥CD,不符合题意;
②∵∠3=∠4,
∴BC∥AD,符合题意;
③∵AB∥CD,
∴∠B+∠BCD=180°,
∵∠ADC=∠B,
∴∠ADC+∠BCD=180°,由同旁内角互补,两直线平行可得BC∥AD,故符合题意;
④∵AB∥CE,
∴∠B+∠BCD=180°,
∵∠BCD=∠BAD,
∴∠B+∠BAD=180°,由同旁内角互补,两直线平行可得BC∥AD,故符合题意;
故能推出BC∥AD的条件为②③④.
故选:D.
8.【解答】解:①负数有立方根,原命题是假命题;
②一个实数的算术平方根一定是非负数,原命题是假命题;
③一个正数或负数的立方根与这个数同号,原命题是真命题;
④如果一个数的算术平方根是这个数本身,那么这个数是1或0,原命题是真命题;
⑤如果一个数的立方根是这个数本身,那么这个数是1、﹣1或0,原命题是假命题;
故选:B.
9.【解答】解:如图,
∵AE∥CF,∠A=50°,
∴∠1=∠A=50°,
∵AB∥CD,
∴∠C=∠1=50°,
故选:B.
10.【解答】解:因为平行于同一条直线的两条直线互相平行,故选项A正确;
垂直于一条直线a的直线,必垂直于a的平行线b,故选项B正确;
垂直于同一条直线的两条直线互相平行,故选项C错误、D正确.
故选:C.
二.填空题(共5小题)
11.【解答】解:有两种情况:
①如图①所示,直线a与c之间的距离是5+2=7;
②如图②所示,直线a与c之间的距离是5﹣2=3;
综上所述,a与c之间的距离为7或3.
故答案为:7或3.
12.【解答】解:如图,∵∠1=110°,
∴∠AGD=180°﹣110°=70°,
∵CD∥BE,
∴∠B=∠AGD=70°.
故答案为:70°.
13.【解答】解:由折叠的性质得出∠GFE=∠EFC=72°,
则∠BFG=36°,
∵四边形ABCD是长方形,
∴AD∥BC,
∴∠FGE=36°,
∴∠EGH=54°.
故答案为:54°.
14.【解答】解:∵∠A=40°,∠C=80°,
∴∠B=180°﹣∠A﹣∠C=180°﹣40°﹣80°=60°,
∵DE∥BC,
∴∠ADE=∠B=60°.
故答案为:60.
15.【解答】解:如图,过点B作BD∥a,
∴∠ABD=∠1=22°,
∵a∥b,
∴BD∥b,
∴∠2=∠DBC=∠ABC﹣∠ABD=60°﹣22°=38°.
故答案为:38°.
三.解答题(共4小题)
16.【解答】解:∵BE∥FG,
∴∠EBC=∠1,
∵∠1=∠2,
∴∠EBC=∠2,
∴DE∥BC,
∴∠ADE=∠ABC=40°.
17.【解答】证明:如图,过E作EF∥AB,
∴∠B=∠3,
∵∠1=∠B,
∴∠1=∠3.
∵BE⊥DE,
∴∠3+∠4=90°,
∴∠1+∠2=180°﹣(∠3+∠4)=90°,
∴∠2=∠4,
∵AB∥CD,EF∥AB,
∴EF∥CD,
∴∠4=∠D.
∴∠2=∠D.
18.【解答】(1)证明:∵∠A+∠3=180°,
∴AE∥GF,
∴∠2=∠A,
∵∠1=∠2,
∴∠1=∠A,
∴AB∥CD;
(2)解:∵AB∥CD,
∴∠D+∠ABD=180°,
∴∠D+∠CBD+∠CBA=180°,
∵∠D=80°,∠CBD=70°,
∴∠CBA=180°﹣∠D﹣∠CBD
=180°﹣80°﹣70°
=30°.
19.【解答】解:(1)∵AB∥CD,
∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵∠PAB=120°,∠PCD=130°,
∴∠APE=60°,∠CPE=50°,
∴∠APC=∠APE+∠CPE=110°.
故答案为110°.
(2)①当点P在A、B两点之间,如图3,作PQ∥AD,
∵PQ∥AD,AD∥BC,
∴PQ∥AD∥BC,
∴∠DPQ=∠β,∠CPQ=∠γ,
∵∠CPD=∠DPQ+∠CPQ,
∴∠α=∠β+∠γ;
②当点P在B、O两点之间时,作PQ∥AD,
∵PQ∥AD,AD∥BC,
∴PQ∥AD∥BC,
∴∠DPQ=∠β,∠CPQ=∠γ,
∵∠CPD=∠DPQ﹣∠CPQ,
∴∠α=∠β﹣∠γ.
一.选择题
1.能说明命题“若x2≥4,则x≥2”为假命题的一个反例可以是( )
A.x=﹣1 B.x=2 C.x=﹣3 D.x=5
2.如果两个角的两边分别平行,而其中一个角比另一个角的3倍少20°,那么这两个角是( )
A.50°、130° B.都是10°
C.50°、130°或10°、10° D.以上都不对
3.下列命题错误的是( )
A.长度为 5,2,3 的三条线段可以组成三角形
B.任意三角形的内角和都是 180°
C.多边形的外角和是 360°
D.两直线平行,同位角相等
4.如图,已知AB∥CD,∠A=60°,∠ECD=120°,∠ECA的度数是( )
A.90° B.120° C.135° D.150°
5.如图,已知AB∥CD,HI∥FG,EF⊥CD于F,∠1=40°,那么∠EHI=( )
A.60° B.50° C.45° D.40°
6.下列命题正确的是( )
A.有两边和一角分别相等的两个三角形全等
B.一个多边形的内角和是它的外角和的2倍,则这个多边形是七边形
C.一组对边平行且一组对角相等的四边形是平行四边形
D.相等的圆心角所对的弧也相等
7.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③AB∥CE且∠ADC=∠B;④AB∥CE且∠BCD=∠BAD;其中能推出BC∥AD的条件为( )
A.①② B.②④ C.②③ D.②③④
8.下列命题:
①负数没有立方根;
②一个实数的算术平方根一定是正数;
③一个正数或负数的立方根与这个数同号;
④如果一个数的算术平方根是这个数本身,那么这个数是1或0;
⑤如果一个数的立方根是这个数本身,那么这个数是1或0,其中错误的有( )
A.2个 B.3个 C.4个 D.5个
9.如图,AB∥CD,AE∥CF,∠A=50°,则∠C=( )
A.40° B.50° C.60° D.70°
10.a,b,c是同一平面内的三条直线,下列说法错误的是( )
A.如果a∥b,b∥c,那么a∥c B.如果a∥b,b⊥c,那么a⊥c
C.如果a⊥c,b⊥c,那么a⊥b D.如果a⊥b,b⊥c,那么a∥c
二.填空题
11.在同一平面内,设a、b、c是三条互相平行的直线,a与b之间的距离为5,b与c之间的距离为2,则a与c之间的距离为 .
12.如图,已知∠1=110°,如果CD∥BE,那么∠B的度数为 .
13.如图,将一个长方形纸片ABCD沿EF折叠,点C恰好落在AD边上点G处,点D落在点H处.若∠CFE=72°,则∠EGH的度数为 .
14.已知,如图,点D,E分别在AB和AC上,且DE∥BC,∠A=40°,∠C=80°,则∠ADE= 度.
15.已知直线a∥b,将一块含30°角的直角三角板ABC按如图所示方式放置(∠BAC=30°),并且顶点A,C分别落在直线a,b上,若∠1=22°,则∠2的度数是 .
三.解答题
16.如图,已知BE∥FG,∠1=∠2,∠ABC=40°,试求∠ADE的度数.
17.如图,AB∥CD,点E在AC上,∠1=∠B,BE⊥DE,试说明∠2=∠D.
18.如图,已知∠A+∠3=180°,∠1=∠2,∠D=80°,∠CBD=70°.
(1)试说明AB∥CD;
(2)求∠CBA的度数.
19.问题迁移:
①如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,设∠CPD=∠α,∠ADP=∠β,∠BCP=∠γ,问:∠α、∠β、∠γ之间有何数量关系?请说明理由.
②在①的条件下,如果点P不在A、B两点之间运动时(点P与点A、B、O三点不重合),请你直接写出∠α、∠β、∠γ间的数量关系.
参考答案与试题解析
一.选择题
1.【解答】解:说明命题“若x2≥4,则x≥2”是假命题的一个反例可以是x=﹣3.
故选:C.
2.【解答】解:∵两个角的两边分别平行,
∴这两个角相等或互补.
设其中一角为x°,
若这两个角相等,则x=3x﹣20,
解得:x=10,
∴这两个角的度数是10°和10°;
若这两个角互补,
则180﹣x=3x﹣20,
解得:x=50,
∴这两个角的度数是50°和130°.
∴这两个角的度数是50°、130°或10°、10°.
故选:C.
3.【解答】解:A、因为2+3=5,所以长度为 5,2,3 的三条线段不可以组成三角形,原命题是错误,符合题意;
B、任意三角形的内角和都是 180°,原命题是正确,不符合题意;
C、多边形的外角和是 360°,原命题是正确,不符合题意;
D、两直线平行,同位角相等,原命题是正确,不符合题意;
故选:A.
4.【解答】解:∵AB∥CD,∠A=60°,
∴∠A+∠ACD=180°,
∴∠ACD=120°,
∵∠ECD=120°,
∴∠ECA=360°﹣∠ECD﹣∠ACD=360°﹣120°﹣120°=120°,
故选:B.
5.【解答】解:∵AB∥CD,∠1=40°,
∴∠GFD=∠1=40°,
∵EF⊥CD,
∴∠EFD=90°,
∴∠EFG=∠EFD﹣∠GFD=90°﹣40°=50°,
又∵HI∥FG,
∴∠EHI=∠EFG=50°,
故选:B.
6.【解答】解:A、有两边和其夹角分别相等的两个三角形全等,原命题是假命题;
B、一个多边形的内角和是它的外角和的2倍,则这个多边形是六边形,原命题是假命题;
C、一组对边平行且相等的四边形是平行四边形,原命题是假命题;
D、相等的圆心角所对的弧也相等,是真命题;
故选:D.
7.【解答】解:①∵∠1=∠2,
∴AB∥CD,不符合题意;
②∵∠3=∠4,
∴BC∥AD,符合题意;
③∵AB∥CD,
∴∠B+∠BCD=180°,
∵∠ADC=∠B,
∴∠ADC+∠BCD=180°,由同旁内角互补,两直线平行可得BC∥AD,故符合题意;
④∵AB∥CE,
∴∠B+∠BCD=180°,
∵∠BCD=∠BAD,
∴∠B+∠BAD=180°,由同旁内角互补,两直线平行可得BC∥AD,故符合题意;
故能推出BC∥AD的条件为②③④.
故选:D.
8.【解答】解:①负数有立方根,原命题是假命题;
②一个实数的算术平方根一定是非负数,原命题是假命题;
③一个正数或负数的立方根与这个数同号,原命题是真命题;
④如果一个数的算术平方根是这个数本身,那么这个数是1或0,原命题是真命题;
⑤如果一个数的立方根是这个数本身,那么这个数是1、﹣1或0,原命题是假命题;
故选:B.
9.【解答】解:如图,
∵AE∥CF,∠A=50°,
∴∠1=∠A=50°,
∵AB∥CD,
∴∠C=∠1=50°,
故选:B.
10.【解答】解:因为平行于同一条直线的两条直线互相平行,故选项A正确;
垂直于一条直线a的直线,必垂直于a的平行线b,故选项B正确;
垂直于同一条直线的两条直线互相平行,故选项C错误、D正确.
故选:C.
二.填空题(共5小题)
11.【解答】解:有两种情况:
①如图①所示,直线a与c之间的距离是5+2=7;
②如图②所示,直线a与c之间的距离是5﹣2=3;
综上所述,a与c之间的距离为7或3.
故答案为:7或3.
12.【解答】解:如图,∵∠1=110°,
∴∠AGD=180°﹣110°=70°,
∵CD∥BE,
∴∠B=∠AGD=70°.
故答案为:70°.
13.【解答】解:由折叠的性质得出∠GFE=∠EFC=72°,
则∠BFG=36°,
∵四边形ABCD是长方形,
∴AD∥BC,
∴∠FGE=36°,
∴∠EGH=54°.
故答案为:54°.
14.【解答】解:∵∠A=40°,∠C=80°,
∴∠B=180°﹣∠A﹣∠C=180°﹣40°﹣80°=60°,
∵DE∥BC,
∴∠ADE=∠B=60°.
故答案为:60.
15.【解答】解:如图,过点B作BD∥a,
∴∠ABD=∠1=22°,
∵a∥b,
∴BD∥b,
∴∠2=∠DBC=∠ABC﹣∠ABD=60°﹣22°=38°.
故答案为:38°.
三.解答题(共4小题)
16.【解答】解:∵BE∥FG,
∴∠EBC=∠1,
∵∠1=∠2,
∴∠EBC=∠2,
∴DE∥BC,
∴∠ADE=∠ABC=40°.
17.【解答】证明:如图,过E作EF∥AB,
∴∠B=∠3,
∵∠1=∠B,
∴∠1=∠3.
∵BE⊥DE,
∴∠3+∠4=90°,
∴∠1+∠2=180°﹣(∠3+∠4)=90°,
∴∠2=∠4,
∵AB∥CD,EF∥AB,
∴EF∥CD,
∴∠4=∠D.
∴∠2=∠D.
18.【解答】(1)证明:∵∠A+∠3=180°,
∴AE∥GF,
∴∠2=∠A,
∵∠1=∠2,
∴∠1=∠A,
∴AB∥CD;
(2)解:∵AB∥CD,
∴∠D+∠ABD=180°,
∴∠D+∠CBD+∠CBA=180°,
∵∠D=80°,∠CBD=70°,
∴∠CBA=180°﹣∠D﹣∠CBD
=180°﹣80°﹣70°
=30°.
19.【解答】解:(1)∵AB∥CD,
∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵∠PAB=120°,∠PCD=130°,
∴∠APE=60°,∠CPE=50°,
∴∠APC=∠APE+∠CPE=110°.
故答案为110°.
(2)①当点P在A、B两点之间,如图3,作PQ∥AD,
∵PQ∥AD,AD∥BC,
∴PQ∥AD∥BC,
∴∠DPQ=∠β,∠CPQ=∠γ,
∵∠CPD=∠DPQ+∠CPQ,
∴∠α=∠β+∠γ;
②当点P在B、O两点之间时,作PQ∥AD,
∵PQ∥AD,AD∥BC,
∴PQ∥AD∥BC,
∴∠DPQ=∠β,∠CPQ=∠γ,
∵∠CPD=∠DPQ﹣∠CPQ,
∴∠α=∠β﹣∠γ.
