人教版数学七年级下册 第10章 10.2 直方图同步测试试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学七年级下册 第10章 10.2 直方图同步测试试题(一)(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 274.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-27 00:00:00 | ||
图片预览




文档简介
直方图同步测试试题(一)
一.选择题
1.一个容量为80的样本,其最大值是133,最小值是51.若确定组距为10,则可以分成( )
A.10组 B.9组 C.8组 D.7组
2.下列说法:①两点之间,线段最短;②正数和负数统称为有理数;③多项式3x2﹣5x2y2﹣6y4﹣2是四次四项式;④一个容量为80的样本最大值是123,最小值是50,取组距为10,则可以分成7组;⑤一个锐角的补角与这个角的余角的差是直角,其中正确的有( )
A.2个 B.3个 C.4个 D.5个
3.有100个数据,落在某一小组内的频数与总数之比是0.4,那么在这100个数据中,落在这一小组内的数据的频数是( )
A.100 B.40 C.20 D.4
4.小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:
通话时间x/分钟 0<x≤5 5<x≤10 10<x≤15 15<x≤20
频数(通话次数) 20 16 9 5
则5月份通话次数中,通话时间不超过15分钟的所占百分比是( )
A.10% B.40% C.50% D.90%
5.在画频数分布直方图时,一组数据的最小值为149,最大值为172.若确定组距为3,则分成的组数是( )
A.8 B.7 C.6 D.5
6.如图所示是某初级中学七年级(2)班的数学成绩统计图,下列说法错误的是( )
A.该班的总人数为40
B.得分在70~80分之间的人数最多
C.及格(≥60分)人数是26
D.得分在90~100分之间的人数最少
7.某棉纺厂为了解一批棉花的质量,从中随机抽取了20根棉花纤维进行测量,其长度x(单位:mm)的数据分布如下表所示,则棉花纤维长度的数据在24≤x<32这个范围的频数为( )
棉花纤维长度x 频数
0≤x<8 1
8≤x<16 2
16≤x<24 8
24≤x<32
32≤x<40 3
A.6 B.7 C.4 D.2
8.某班45名学生的成绩被分为5组,第1~4组的频数分别为12,11,9,4,则第5组的频率是( )
A.0.1 B.0.2 C.0.3 D.0.4
9.张山统计了他家今年3月份打电话的次数及通话时间,并列出如下频数分布表:
通话时间x(分钟) 0<x≤5 5<x≤10 10<x≤15 15<x≤20
频数(通话次数 20 16 9 5
则通话时间不超过15分钟的频率是( )
A.0.4 B.0.6 C.0.7 D.0.9
10.某小区居民利用“健步行APP”开展健步走活动,为了解居民的健步走情况,小文同学调查了部分居民某天行走的步数(单位:千步),并将样本数据整理绘制成如下不完整的频数分布直方图和扇形统计图.
有下面四个推断:
①小文此次一共调查了200位小区居民;
②行走步数为8~12千步的人数超过调查总人数的一半;
③行走步数为4~8千步的人数为50人;
④行走步数为12~16千步的扇形圆心角是72°.
根据统计图提供的信息,上述推断合理的是( )
A.①②③ B.①②④ C.①③④ D.②③④
二.填空题
11.样本的50个数据分别落在4个组内,第1、2、4组数据的个数分别是6、12、22,则落在第3组的频数是 .
12.小明同学按照老师要求对本班40名学生的血型进行了统计,列出如下的统计表.则本班A型血的人数是 .
组别 A型 B型 AB型 O型
频率
0.35 0.1 0.15
13.把64个数据分成8组,从第1组到第4组的频数分别是6,9,12,14,第5组到第7组的频率和是0.25,那么第8组的频数是 .
14.某学校为了解本校2000名学生的课外阅读情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成如下的统计表,根据表中信息估计全校每周课外阅读时间不超过2小时的学生有 人.
每周课外阅读时间x(小时) 0≤x≤1 1<x≤2 2<x≤3 x>3
人数 7 10 14 19
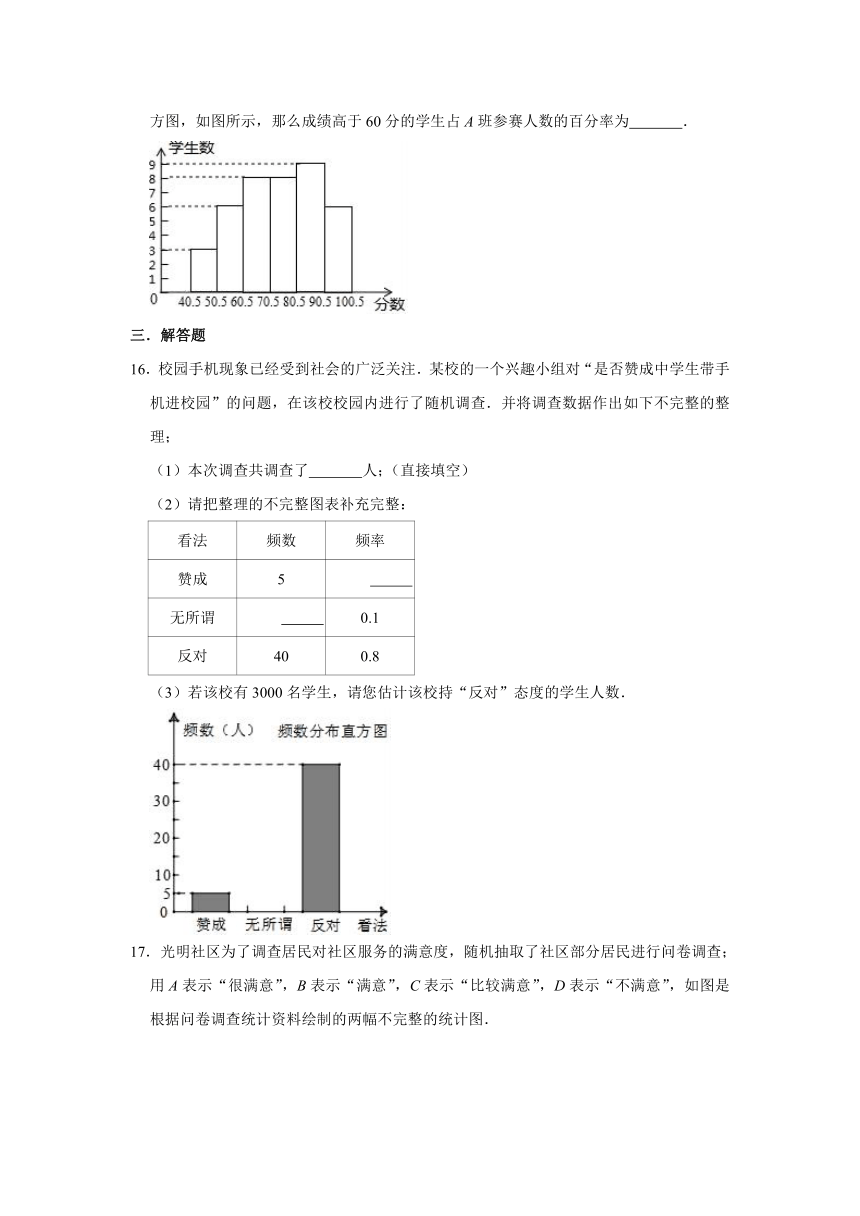
15.A班学生参加“垃圾分类知识”竞赛,已知竞赛得分都是整数,竞赛成绩的频数分布直方图,如图所示,那么成绩高于60分的学生占A班参赛人数的百分率为 .
三.解答题
16.校园手机现象已经受到社会的广泛关注.某校的一个兴趣小组对“是否赞成中学生带手机进校园”的问题,在该校校园内进行了随机调查.并将调查数据作出如下不完整的整理;
(1)本次调查共调查了 人;(直接填空)
(2)请把整理的不完整图表补充完整:
看法 频数 频率
赞成 5
无所谓 0.1
反对 40 0.8
(3)若该校有3000名学生,请您估计该校持“反对”态度的学生人数.
17.光明社区为了调查居民对社区服务的满意度,随机抽取了社区部分居民进行问卷调查;用A表示“很满意”,B表示“满意”,C表示“比较满意”,D表示“不满意”,如图是根据问卷调查统计资料绘制的两幅不完整的统计图.
请你根据统计图提供的信息解答以下问题:
(1)本次问卷调查共调查了多少个居民?
(2)求出调查结果为A的人数,并将直方图中A部分的图形补充完整;
(3)如果该社区有居民5000人,请你估计对社区服务感到“不满意”的居民约有多少人?
18.某校传统文化社团某天进行纳新活动,组织初一新生选报兴趣学社,由于当天报名人数较多,从现场随机抽查部分学生的报名意向进行统计,并绘制出不完全的频数分布表和频数分布直方图,如下所示:
传统文化 学社 报名频数
(人数) 报名
频率 录取率
灯谜 12 p p+0.05
书法 27 0.45 0.4
剪纸 m 0.3 p+t+0.35
南音 n t t+0.75
请根据上述图表,完成下列各题:
(1)填空:m= ,n= ,p+t= ,现场共抽查了 名学生;
(2)请把条形统计图补充完整;
(3)现有1200个学生报名参加该校传统文化社团,则可以估计被剪纸学社录取的学生数比南音学社录取的学生数多了多少人?若把所有被录取人数按表中学社制作成扇形统计图,则被灯谜学社录取的学生数的扇形圆心角为多少度?
19.为了弘扬中华传统文化,某校组织八年级800名学生参加汉字听写大赛,为了了解学生整体听写能力,从中抽取部分学生的成绩进行统计分析,得到如图所示的频数分布表:
分数段 50.5﹣60.5 60.5﹣70.5 70.5﹣80.5 80.5﹣90.5 90.5﹣100.5
频数 16 30 50 m 24
所占百分比 8% 15% 25% 40% n
请根据尚未完成的表格,解答下列问题:
(1)本次抽样调查,一共调查 名学生的成绩,表中n= ;
(2)补全图中所示的频数分布直方图;
(3)若成绩超过80分为优秀,则该校八年级学生中汉字听写能力优秀的约有多少人?
参考答案与试题解析
一.选择题
1.【解答】解:∵最大值为133,最小值为51,
∴最大值与最小值的差是133﹣51=82,
∵组距为10,=8.2,
∴可以分成9组.
故选:B.
2.【解答】解:①两点之间,线段最短,此结论正确;
②正有理数、负有理数和0统称为有理数,此结论错误;
③多项式3x2﹣5x2y2﹣6y4﹣2是四次四项式,此结论正确;
④一个容量为80的样本最大值是123,最小值是50,取组距为10,则可以分成8组,此结论错误;
⑤一个锐角的补角与这个角的余角的差是直角,此结论正确;
故选:B.
3.【解答】解:∵一个有100个数据的样本,落在某一小组内的频率是0.4,
∴在这100个数据中,落在这一小组内的频数是:100×0.4=40.
故选:B.
4.【解答】解:5月份通话次数中,通话时间不超过15分钟的所占百分比是×100%=90%,
故选:D.
5.【解答】解:∵=≈7.7,
∴分成的组数是8组,
故选:A.
6.【解答】解:A、该班的总人数为4+12+14+8+2=40人,此选项正确;
B、得分在70~80分之间的人数最多,有14人,此选项正确;
C、及格(≥60分)人数是12+14+8+2=36人,此选项错误;
D、得分在90~100分之间的人数最少,有2人,此选项正确;
故选:C.
7.【解答】解:棉花纤维长度的数据在24≤x<32这个范围的频数为=20﹣1﹣2﹣8﹣3=6,
故选:A.
8.【解答】解:∵第5组的频数为45﹣(12+11+9+4)=9,
∴第5组的频率是9÷45=0.2,
故选:B.
9.【解答】解:由表格可得,通话时间不超过15分钟的频率是:=0.9,
故选:D.
10.【解答】解:①小文此次一共调查了70÷35%=200位小区居民,正确;
②行走步数为8~12千步的人数为70,未超过调查总人数的一半,错误;
③行走步数为4~8千步的人数为200×25%=50人,正确;
④行走步数为12~16千步的扇形圆心角是360°×20%=72°,正确;
故选:C.
二.填空题(共5小题)
11.【解答】解:第3组数据的频数:50﹣6﹣12﹣22=10,
故答案为:10.
12.【解答】解:本班A型血的人数为:40×(1﹣0.35﹣0.1﹣0.15)=40×0.4=16.
故答案为:16.
13.【解答】解:∵把64个数据分成8组,从第1组到第4组的频数分别是6,9,12,14,第5组到第7组的频率和是0.25,
∴第5组到第7组的频数和为:64×0.25=16,
∴第8组的频数是:64﹣6﹣9﹣12﹣14﹣16=7.
故答案为:7.
14.【解答】解:2000×=680,
所以估计全校每周课外阅读时间不超过2小时的学生有680人.
故答案为680.
15.【解答】解:=77.5%,
故答案为:77.5%.
三.解答题(共4小题)
16.【解答】解:(1)观察统计表知道:反对的频数为40,频率为0.8,
故调查的人数为:40÷0.8=50(人);
看法 频数 频率
赞成 5 0.1
5 0.1
反对 40 0.8
故答案为:50;
(2)无所谓的频数为:50﹣5﹣40=5(人),
赞成的频率为:1﹣0.1﹣0.8=0.1;
统计图为:
(3)0.8×3000=2400(人),
答:该校持“反对”态度的学生人数是2400人.
17.【解答】解:(1)94÷47%=200(人),
答:本次问卷调查共调查了200个居民;
(2)调查结果为A的人数为200×30%=60(人),
C等级人数为200×13%=26(人),D等级人数为200﹣(60+94+26)=20(人),
补全统计图如下:
(3)估计对社区服务感到“不满意”的居民约有5000×10%=500(人).
18.【解答】解:(1)现场抽查的总人数为27÷0.45=60,
m=60×0.3=18,p=12÷60=0.2,
则t=1﹣(0.2+0.45+0.3)=0.05,
∴n=60×0.05=3,
∴p+t=0.25,
故答案为:18、3、0.25、60;
(2)由(1)知,m=18,n=3,
补全的条形统计图如下所示:
(3)被剪纸学社录取的学生数比南音学社录取的学生数多了:1200×0.3×(0.2+0.05+0.35)﹣1200×0.05×(0.05+0.75)
=360×0.6﹣60×0.8
=216﹣48
=168(人);
灯谜录取的人数为:1200×0.2×(0.2+0.05)=240×0.25=60,
书法录取的人数为:1200×0.45×0.4=216,
剪纸录取的人数为:1200×0.3×(0.2+0.05+0.35)=216,
南音录取的人数为:1200×0.05×(0.05+0.75)=48,
被灯谜学社录取的学生数的扇形圆心角为:360°×=40°
答:被剪纸学社录取的学生数比南音学社录取的学生数多了168人,被灯谜学社录取的学生数的扇形圆心角为40°.
19.【解答】解:(1)样本容量是:16÷0.08=200;
m=200×0.40=80,
n==0.12,
故答案为:200、0.12;
(2)补全频数分布直方图,如下:
(3)800×(0.4+0.12)=416(人).
答:该校八年级学生中汉字听写能力优秀的约有416人.
一.选择题
1.一个容量为80的样本,其最大值是133,最小值是51.若确定组距为10,则可以分成( )
A.10组 B.9组 C.8组 D.7组
2.下列说法:①两点之间,线段最短;②正数和负数统称为有理数;③多项式3x2﹣5x2y2﹣6y4﹣2是四次四项式;④一个容量为80的样本最大值是123,最小值是50,取组距为10,则可以分成7组;⑤一个锐角的补角与这个角的余角的差是直角,其中正确的有( )
A.2个 B.3个 C.4个 D.5个
3.有100个数据,落在某一小组内的频数与总数之比是0.4,那么在这100个数据中,落在这一小组内的数据的频数是( )
A.100 B.40 C.20 D.4
4.小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:
通话时间x/分钟 0<x≤5 5<x≤10 10<x≤15 15<x≤20
频数(通话次数) 20 16 9 5
则5月份通话次数中,通话时间不超过15分钟的所占百分比是( )
A.10% B.40% C.50% D.90%
5.在画频数分布直方图时,一组数据的最小值为149,最大值为172.若确定组距为3,则分成的组数是( )
A.8 B.7 C.6 D.5
6.如图所示是某初级中学七年级(2)班的数学成绩统计图,下列说法错误的是( )
A.该班的总人数为40
B.得分在70~80分之间的人数最多
C.及格(≥60分)人数是26
D.得分在90~100分之间的人数最少
7.某棉纺厂为了解一批棉花的质量,从中随机抽取了20根棉花纤维进行测量,其长度x(单位:mm)的数据分布如下表所示,则棉花纤维长度的数据在24≤x<32这个范围的频数为( )
棉花纤维长度x 频数
0≤x<8 1
8≤x<16 2
16≤x<24 8
24≤x<32
32≤x<40 3
A.6 B.7 C.4 D.2
8.某班45名学生的成绩被分为5组,第1~4组的频数分别为12,11,9,4,则第5组的频率是( )
A.0.1 B.0.2 C.0.3 D.0.4
9.张山统计了他家今年3月份打电话的次数及通话时间,并列出如下频数分布表:
通话时间x(分钟) 0<x≤5 5<x≤10 10<x≤15 15<x≤20
频数(通话次数 20 16 9 5
则通话时间不超过15分钟的频率是( )
A.0.4 B.0.6 C.0.7 D.0.9
10.某小区居民利用“健步行APP”开展健步走活动,为了解居民的健步走情况,小文同学调查了部分居民某天行走的步数(单位:千步),并将样本数据整理绘制成如下不完整的频数分布直方图和扇形统计图.
有下面四个推断:
①小文此次一共调查了200位小区居民;
②行走步数为8~12千步的人数超过调查总人数的一半;
③行走步数为4~8千步的人数为50人;
④行走步数为12~16千步的扇形圆心角是72°.
根据统计图提供的信息,上述推断合理的是( )
A.①②③ B.①②④ C.①③④ D.②③④
二.填空题
11.样本的50个数据分别落在4个组内,第1、2、4组数据的个数分别是6、12、22,则落在第3组的频数是 .
12.小明同学按照老师要求对本班40名学生的血型进行了统计,列出如下的统计表.则本班A型血的人数是 .
组别 A型 B型 AB型 O型
频率
0.35 0.1 0.15
13.把64个数据分成8组,从第1组到第4组的频数分别是6,9,12,14,第5组到第7组的频率和是0.25,那么第8组的频数是 .
14.某学校为了解本校2000名学生的课外阅读情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成如下的统计表,根据表中信息估计全校每周课外阅读时间不超过2小时的学生有 人.
每周课外阅读时间x(小时) 0≤x≤1 1<x≤2 2<x≤3 x>3
人数 7 10 14 19
15.A班学生参加“垃圾分类知识”竞赛,已知竞赛得分都是整数,竞赛成绩的频数分布直方图,如图所示,那么成绩高于60分的学生占A班参赛人数的百分率为 .
三.解答题
16.校园手机现象已经受到社会的广泛关注.某校的一个兴趣小组对“是否赞成中学生带手机进校园”的问题,在该校校园内进行了随机调查.并将调查数据作出如下不完整的整理;
(1)本次调查共调查了 人;(直接填空)
(2)请把整理的不完整图表补充完整:
看法 频数 频率
赞成 5
无所谓 0.1
反对 40 0.8
(3)若该校有3000名学生,请您估计该校持“反对”态度的学生人数.
17.光明社区为了调查居民对社区服务的满意度,随机抽取了社区部分居民进行问卷调查;用A表示“很满意”,B表示“满意”,C表示“比较满意”,D表示“不满意”,如图是根据问卷调查统计资料绘制的两幅不完整的统计图.
请你根据统计图提供的信息解答以下问题:
(1)本次问卷调查共调查了多少个居民?
(2)求出调查结果为A的人数,并将直方图中A部分的图形补充完整;
(3)如果该社区有居民5000人,请你估计对社区服务感到“不满意”的居民约有多少人?
18.某校传统文化社团某天进行纳新活动,组织初一新生选报兴趣学社,由于当天报名人数较多,从现场随机抽查部分学生的报名意向进行统计,并绘制出不完全的频数分布表和频数分布直方图,如下所示:
传统文化 学社 报名频数
(人数) 报名
频率 录取率
灯谜 12 p p+0.05
书法 27 0.45 0.4
剪纸 m 0.3 p+t+0.35
南音 n t t+0.75
请根据上述图表,完成下列各题:
(1)填空:m= ,n= ,p+t= ,现场共抽查了 名学生;
(2)请把条形统计图补充完整;
(3)现有1200个学生报名参加该校传统文化社团,则可以估计被剪纸学社录取的学生数比南音学社录取的学生数多了多少人?若把所有被录取人数按表中学社制作成扇形统计图,则被灯谜学社录取的学生数的扇形圆心角为多少度?
19.为了弘扬中华传统文化,某校组织八年级800名学生参加汉字听写大赛,为了了解学生整体听写能力,从中抽取部分学生的成绩进行统计分析,得到如图所示的频数分布表:
分数段 50.5﹣60.5 60.5﹣70.5 70.5﹣80.5 80.5﹣90.5 90.5﹣100.5
频数 16 30 50 m 24
所占百分比 8% 15% 25% 40% n
请根据尚未完成的表格,解答下列问题:
(1)本次抽样调查,一共调查 名学生的成绩,表中n= ;
(2)补全图中所示的频数分布直方图;
(3)若成绩超过80分为优秀,则该校八年级学生中汉字听写能力优秀的约有多少人?
参考答案与试题解析
一.选择题
1.【解答】解:∵最大值为133,最小值为51,
∴最大值与最小值的差是133﹣51=82,
∵组距为10,=8.2,
∴可以分成9组.
故选:B.
2.【解答】解:①两点之间,线段最短,此结论正确;
②正有理数、负有理数和0统称为有理数,此结论错误;
③多项式3x2﹣5x2y2﹣6y4﹣2是四次四项式,此结论正确;
④一个容量为80的样本最大值是123,最小值是50,取组距为10,则可以分成8组,此结论错误;
⑤一个锐角的补角与这个角的余角的差是直角,此结论正确;
故选:B.
3.【解答】解:∵一个有100个数据的样本,落在某一小组内的频率是0.4,
∴在这100个数据中,落在这一小组内的频数是:100×0.4=40.
故选:B.
4.【解答】解:5月份通话次数中,通话时间不超过15分钟的所占百分比是×100%=90%,
故选:D.
5.【解答】解:∵=≈7.7,
∴分成的组数是8组,
故选:A.
6.【解答】解:A、该班的总人数为4+12+14+8+2=40人,此选项正确;
B、得分在70~80分之间的人数最多,有14人,此选项正确;
C、及格(≥60分)人数是12+14+8+2=36人,此选项错误;
D、得分在90~100分之间的人数最少,有2人,此选项正确;
故选:C.
7.【解答】解:棉花纤维长度的数据在24≤x<32这个范围的频数为=20﹣1﹣2﹣8﹣3=6,
故选:A.
8.【解答】解:∵第5组的频数为45﹣(12+11+9+4)=9,
∴第5组的频率是9÷45=0.2,
故选:B.
9.【解答】解:由表格可得,通话时间不超过15分钟的频率是:=0.9,
故选:D.
10.【解答】解:①小文此次一共调查了70÷35%=200位小区居民,正确;
②行走步数为8~12千步的人数为70,未超过调查总人数的一半,错误;
③行走步数为4~8千步的人数为200×25%=50人,正确;
④行走步数为12~16千步的扇形圆心角是360°×20%=72°,正确;
故选:C.
二.填空题(共5小题)
11.【解答】解:第3组数据的频数:50﹣6﹣12﹣22=10,
故答案为:10.
12.【解答】解:本班A型血的人数为:40×(1﹣0.35﹣0.1﹣0.15)=40×0.4=16.
故答案为:16.
13.【解答】解:∵把64个数据分成8组,从第1组到第4组的频数分别是6,9,12,14,第5组到第7组的频率和是0.25,
∴第5组到第7组的频数和为:64×0.25=16,
∴第8组的频数是:64﹣6﹣9﹣12﹣14﹣16=7.
故答案为:7.
14.【解答】解:2000×=680,
所以估计全校每周课外阅读时间不超过2小时的学生有680人.
故答案为680.
15.【解答】解:=77.5%,
故答案为:77.5%.
三.解答题(共4小题)
16.【解答】解:(1)观察统计表知道:反对的频数为40,频率为0.8,
故调查的人数为:40÷0.8=50(人);
看法 频数 频率
赞成 5 0.1
5 0.1
反对 40 0.8
故答案为:50;
(2)无所谓的频数为:50﹣5﹣40=5(人),
赞成的频率为:1﹣0.1﹣0.8=0.1;
统计图为:
(3)0.8×3000=2400(人),
答:该校持“反对”态度的学生人数是2400人.
17.【解答】解:(1)94÷47%=200(人),
答:本次问卷调查共调查了200个居民;
(2)调查结果为A的人数为200×30%=60(人),
C等级人数为200×13%=26(人),D等级人数为200﹣(60+94+26)=20(人),
补全统计图如下:
(3)估计对社区服务感到“不满意”的居民约有5000×10%=500(人).
18.【解答】解:(1)现场抽查的总人数为27÷0.45=60,
m=60×0.3=18,p=12÷60=0.2,
则t=1﹣(0.2+0.45+0.3)=0.05,
∴n=60×0.05=3,
∴p+t=0.25,
故答案为:18、3、0.25、60;
(2)由(1)知,m=18,n=3,
补全的条形统计图如下所示:
(3)被剪纸学社录取的学生数比南音学社录取的学生数多了:1200×0.3×(0.2+0.05+0.35)﹣1200×0.05×(0.05+0.75)
=360×0.6﹣60×0.8
=216﹣48
=168(人);
灯谜录取的人数为:1200×0.2×(0.2+0.05)=240×0.25=60,
书法录取的人数为:1200×0.45×0.4=216,
剪纸录取的人数为:1200×0.3×(0.2+0.05+0.35)=216,
南音录取的人数为:1200×0.05×(0.05+0.75)=48,
被灯谜学社录取的学生数的扇形圆心角为:360°×=40°
答:被剪纸学社录取的学生数比南音学社录取的学生数多了168人,被灯谜学社录取的学生数的扇形圆心角为40°.
19.【解答】解:(1)样本容量是:16÷0.08=200;
m=200×0.40=80,
n==0.12,
故答案为:200、0.12;
(2)补全频数分布直方图,如下:
(3)800×(0.4+0.12)=416(人).
答:该校八年级学生中汉字听写能力优秀的约有416人.
